Бесконтактное выявление и оценка глубины питинговых коррозионных повреждений стенок металлических изделий магнитным методом



На сегодняшний день технология MFL (Magnetic Flux Leakage — технология магнитного вида неразрушающего контроля, использующая, в соответствии с ГОСТ Р 55612–2013, метод эффекта Холла для анализа магнитного поля рассеивания дефекта) широко применяется ведущими компаниями, т. к. при ее использовании не требуется специальная подготовка поверхности металла и допускается наличие изолирующих покрытий (лакокрасочных, эпоксидных и др.) толщиной до 5 мм.

Основной целью контроля MFL дефектоскопом является оперативное выявление дефектов на первоначальном этапе их формирования, для исключения предпосылок техногенных катастроф. Следовательно, необходимо выявлять дефекты глубиной не более 10…30 % от толщины днища. На сегодняшний день ни один из существующих MFL — дефектоскопов не способен гарантированно выявлять дефекты глубиной до 30 % утонения во всем диапазоне толщин от 4 до 16 мм.

Метод рассеянного (вытесненного) магнитного потока является одним из основных методов магнитного вида НК для выявления:

– механических повреждений (продольных или поперечных разрывов или трещин с большим раскрытием) бесшовных и сварных труб, в том числе толстостенных;

– дефектов продольных сварных швов труб [1].

Рассмотрим возможность его применения для выявления питтинговых коррозионных повреждений листовых ферромагнитных материалов под диэлектрическими защитными покрытиями.

При расположении П — образного постоянного магнита на некотором расстоянии от стенки ферромагнитного изделия часть силовых линий прерывается на границе разделов двух сред (магнит — воздух и воздух — стенка изделия) с отличающимися значениями магнитной проницаемости µ_i [2].

Нормальная H_ni (к поверхности раздела) составляющая напряженности магнитного поля испытывает скачок при переходе из одной среды в другую, а тангенциальные составляющие изменяются при переходе через границу раздела сред непрерывно.

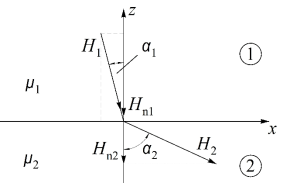
Рис. 1. Преломление (скачок) силовых линий на границе раздела двух сред

При использовании редкоземельных магнитов (Nd-Fe-B) с индукцией порядка 1 … 1,1 Тл достигаемое высокое значение магнитной проницаемости µ_ст низкоуглеродистых сталей приводит к тому, что снаружи на границе раздела воздух/сталь магнитные силовые линии направлены практически перпендикулярно к поверхности, в то время как в объеме изделия они стремятся проходить практически параллельно поверхности, что обеспечивает минимальное сопротивление магнитной цепи [1,2].

На рис. 2 приведена картина магнитного поля П-образного постоянного магнита над плоским ферромагнитным листом с относительной магнитной проницаемостью µ_ст. При определенных соотношениях толщины стенки и размеров магнита практически все силовые линии магнитного потока будут проходить внутри стенки изделия, лишь незначительная часть из них выйдет с противоположной стороны стенки, что иллюстрируется вырезкой А [1].

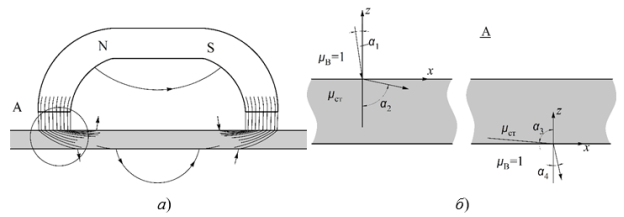
Рис. 2. Картина силовых линий магнитного поля П-образного магнита над плоским ферромагнитным листом (а) и, увеличенно, участка А под полюсом магнита (б)

В случае если на одной из поверхностей листа будет участок с локальным утонением (например, питтинговой коррозией), то произойдет изменение картины магнитного поля (рис. 3).

Плотность силовых линий в районе дефекта возрастет, и часть магнитных силовых линий выйдет из листа, как со стороны установки магнита, так и с противоположной стороны (произойдет рассеяние магнитного потока), что может быть зафиксировано путем измерения нормальной составляющей напряженности магнитного поля Н_i или магнитного потока Ф_i, пронизывающего индукционную обмотку площадью S:

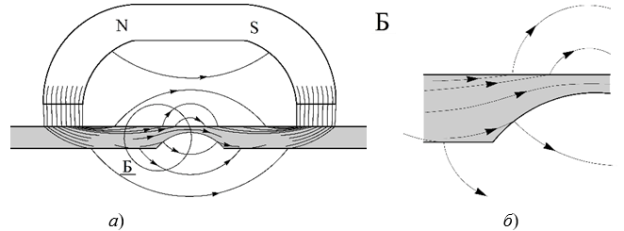
Рис. 3. Картина силовых линий над плоским ферромагнитным листом с утонением (а) и, увеличенно, участка Б в районе дефекта (б)

Первичные измерительные преобразователи (в дальнейшем преобразователи), реализующие рассматриваемый метод, представляют собой П — образные магнитопроводы с вставками из постоянных редкоземельных магнитов (Nd-Fe-B) и многоканальную систему чувствительных элементов, располагаемых симметрично между полюсами магнитопровода в области магнитного поля одной интенсивности (рис. 4).

Базовые преобразователи имеют следующие размеры: длина магнита А = 25 мм, высота магнита С = 10 мм, высота ярма Е = 20 мм, высота полюса D = 25 мм, расстояние между полюсами L = 50 мм, зазор Z = 5 мм. Ширина магнитопровода составляет порядка 40 мм. Преобразователи предназначены для выявления плоскостной и питтинговой коррозии изделий с толщиной стенки Т = 6–16 мм. При l ≈ H гарантированно выявляются искусственные дефекты глубиной от h = 1,8 мм (Т = 6 мм) до h = 8 мм (Т = 16 мм). В качестве чувствительных элементов используются преобразователи Холла, анализирующие изменение нормальной составляющей B_z магнитной индукции в точке наблюдения при перемещении преобразователя относительно дефекта вдоль оси х (начало системы координат связано с центром пропила) [1,2,3].

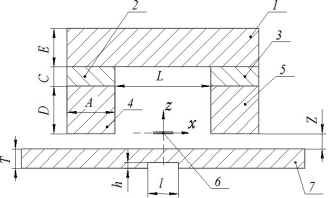
Рис. 4. Структура первичного измерительного преобразователя, реализующего метод MFL и объект контроля с искусственным дефектом в виде поперечного пропила, имитирующим коррозионное повреждение стенки (1 — ярмо магнитопровода, 2 и 3 — редкоземельные магниты, 4 и 5 — полюса магнитопровода, 6 — чувствительный элемент/точка наблюдения, 7 — стальной лист с искусственным дефектом)

Представляется вероятным, что не для всех диапазонов изменения Т и h чувствительность преобразователя, характеризуемая изменением амплитуды B_z (hв зоне коррозионного повреждения, будет оптимальной).

Основные показатели качества преобразователей:

– чувствительность преобразователя d/dh(В_z(h,Т)), определяющая абсолютную погрешность измерения Δh(h, Т), а также диапазон измерения h_{min —} h_max;

– минимально возможные размеры магнитопровода обеспечивающие заданные Δh(h, H) и h_{min —} h_max в требуемом диапазоне толщин Т_{min —} Т_max стенок изделий;

– массогабаритные и эргономические характеристики.

Для обеспечения требуемых показателей качества необходимо искать компромиссное решение, учитывающее взаимосвязанные показатели: диапазон измерения h_{min —} h_max, погрешность измерения Δh(h, Т), диапазон толщин Т_{min —} Т_max и минимально возможные размеры преобразователя [4].

При анализе преобразователя, представленного на рис. 4 будем полагать ширину магнитопровода много больше его высоты С и длины А, что позволяет исключить ее влияние при расчетах.

В настоящее время для решения задач, связанных с распространением электромагнитных полей широко применяются численные методы. Наиболее эффективным и широко используемым методом, является метод конечных элементов

Искомые значения параметров будем рассчитывать в узловых точках (узлах) — общих точках конечных элементов. Скалярный магнитный потенциал φ^M каждого конечного элемента представим в виде полинома, с постоянными в пределах этого элемента коэффициентами

φ^M = a_i + b_ix + c_iy

Основная задача расчета методом конечных элементов — определить коэффициенты a_i, b_i, c_i. После нахождения коэффициентов появляется возможность рассчитать магнитный потенциал в любой точке пространства модели. Исходные данные, дополненные граничными условиями, и энергетические зависимости приводят к системе алгебраических уравнений, которая позволяет рассчитать искомые коэффициенты полиномов во всех конечных элементах [2,3].

Применительно к задачам расчета магнитных статических полей при граничных условиях первого рода (условия Дирихле) минимизируемым функционалом является величина, пропорциональная запасенной в пространстве магнитной энергии:

W_M = 0,5·∫μμ₀H²dv,

где μ — магнитная проницаемость среды, Н — напряженность магнитного поля.

Так как H = -gradφ^M, то минимизируемый функционал можно записать в виде:

W_M = 0,5·∫μμ₀(gradφ^M)²dv,

а искомой (минимизирующей) функцией будет φ^M(ξ, ζ, η), при которой W_M{φ^M}=>min.

В качестве функционала выступает сумма магнитных энергий, накопленных во всех конечных элементах. Как было указано выше, в данной модели элементы соприкасаются в общих, узловых, точках. Энергия элементов определяется магнитными потенциалами узловых точек

W=W{φ₁, φ2… φ_N},

где N — число точек.

На основании анализа и определения магнитных потенциалов общих, узловых, точек, при которых W_M минимальна, формируется система алгебраических уравнений, рассчитываются магнитные потенциалы, вычисляются магнитная индукция и напряженность магнитного поля [2].

Под оптимальными геометрическими характеристиками преобразователя будем понимать такие характеристики и их соотношения, при которых достигается максимальная чувствительность в требуемой области измеряемых h_{min —} h_max контролируемых изделий в диапазоне толщин стенки Т_{min —} Т_max при минимально возможных габаритах.

При использовании программных продуктов, реализующих метод конечных элементов, можно сформулировать следующую постановку задачи расчета преобразователя: двухмерная, осесимметричная, стационарная, в общем случае нелинейная, с открытыми границами со следующими допущениями:

– в достаточно удаленной от преобразователя зоне создаваемое им магнитное поле бесконечно мало;

– отсутствуют внешние магнитные поля;

– модель полностью стационарна (отсутствует временной и температурный дрейф физических характеристик преобразователя).

Согласно первым двум допущениям, в качестве граничных условий для моделей рассматриваемых первичных преобразователей можно назначить граничные условия первого рода (условия Дирихле). В нашей постановке это граничное условие применимо для задания нулевого значения нормальной составляющей вектора магнитной индукции на оси симметрии (в точке наблюдения) и для указания полного затухания поля на условно бесконечно удаленных от преобразователя границах. Варьируемыми параметрами будут толщина пластины Н, относительная координата x* = x/Т, относительная глубина h* = h/Т при постоянной относительной ширине пропила l* = l/Т = 1. При расчетах примем величину зазора Z = 5 мм, а магнитную индукцию в магнитопроводе B_м ≈ 1,12 Тл, соответствующую редкоземельным магнитам [4].

На рис. 5 в качестве примера представлены расчетные зависимости нормальной составляющей B_z(h*, x*) магнитной индукции над листом из стали 1010 толщиной Т = 8 мм с искусственным дефектом в виде поперечного пропила при Z = 5 мм, из которых видно, что максимальное значение B_zm(h*) достигается на краях пропила приx* 0,5.

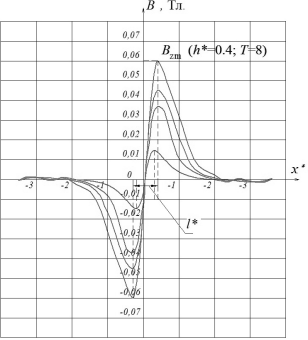
Рис. 5. Зависимость B_z(h*, x*) над листом из стали 1010 толщиной Т = 8 мм в районе поперечного пропила шириной l* =1 при Z = 5 мм

На рис. 6 представлены расчетные зависимости максимального значения B_zm(h*,Т) нормальной составляющей магнитной индукции для рассматриваемой модели преобразователя над ферромагнитным листом из стали 1010 (аналог Ст10) с искусственным дефектом в виде поперечного пропила, выполненным в соответствии с рис. 4.

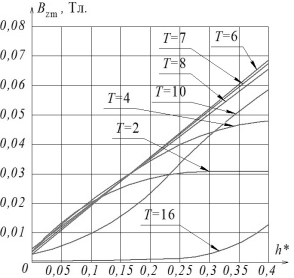
Рис. 6. Зависимость B_zm(h*, Т) над листом из стали 1010 с искусственным дефектом в виде поперечного пропила шириной l* =1 при Z = 5 мм

Из рис. 6 видно, что для чувствительность рассматриваемого преобразователя практически линейна и неизменна в широком диапазоне изменения h* при Т = 6 … 8 мм. Если Т = 2 … 4 мм, то близкие характеристики по чувствительности обеспечиваются до h* =0,15 … 0,2. При увеличении Т более 10мм наблюдается существенное снижение чувствительности преобразователя в области малых значений h*, имитирующих питтинговую коррозию. Расчеты показывают, оптимальными характеристиками преобразователь обладает в диапазоне Т = 5 до 9 мм можно выявлять дефекты в диапазоне h* = 0,05 … 0,4, а наибольшая чувствительность и максимальный диапазон h* достигаются при Т = 7 мм [2,3].

Из рисунка видно, что с использованием рассматриваемых преобразователей возможен контроль питтинговых коррозионных повреждений листовых ферромагнитных материалов в воздушной и водной средах при наличии зазора между магнитной системой и поверхностью листового материала. При пересечении зоны дефект на индукционной обмотке (чувствительном элементе) наведется эдс, площадь которой будет пропорциональна глубине дефекта (питтингового коррозионного повреждения). Для каждого диапазона толщин будут существовать оптимальные габариты измерительного преобразователя. Влияние зазора может быть учтено введением канала магнитоиндукционного толщиномера.

Литература:

1. Потапов А. И., Сясько В. А., Соломенчук П. В. и др. Электромагнитные и магнитные методы неразрушающего контроля материалов и изделий. Т.2: Электромагнитные и магнитные методы дефектоскопии и контроля свойств материалов. СПб.: Нестор-История, 2015. — 440 с.
2. А. И. Потапов, В. А. Сясько, О. П. Пудовкин. Оптимизация параметров первичных измерительных преобразователей, реализующих технологию MFL. «Дефектоскопия» 2015 г. № 8 стр. 64
3. Д. А. Слесарев, А. А. Абакумов. Обработка и представление информации в MFL методе неразрушающего контроля. Дефектоскопия, № 9, 2013 г, с. 3–9
4. Сясько В. А. Об использовании технологии MFL для выявления коррозионных повреждений обшивки судов / В. А. Сясько // В мире неразрушающего контроля. 2015. Т. 18. №. 3. C. 7–10. DOI: 10.12737/12563