Разработана модель и программа для определения состава фаз в системе шлак-раствор-газовая фаза. Определено взаимодействие расплава стали со шлаками, газовой фазой и футеровкой. Модели могут быть использованы для расчетов процессов рафинирования при плавке сталей, а также при дуговой сварке сталей и чугунов.

Ключевые слова: термодинамическая модель, расплав стали, дуговая сварка, рафинирование.

Плавление стали характеризуется большим разнообразием протекающих процессов взаимодействия составляющих системы и большим количеством решаемых задач. Существующие программные средства для моделирования процессов плавки ориентированы на решение отдельных задач, без учета всего комплекса протекающих процессов. В данной работе рассматривается модель процесса плавки стали, позволяющая учесть весь комплекс одновременно протекающих процессов.

Рассмотрим систему, содержащую шлак-раствор-газовую фазу на рис. 1.

Рис. 1. Схема процесса плавки стали: 1 — расплав; 2 — шлак; 3 — газовая фаза; 4 — нановключения; 5 — футеровка

Пусть в системе шлак-расплав-газовая фаза присутствует n-компонентов, а также 3 фазы (f=3): шлак, расплав и газовая фаза. Тогда число степеней свободы (С) согласно правилу фаз Гиббса будет равно С=n–f+2. При f=3 получим C=n–1. Если в качестве одной степени свободы зафиксировать температуру, то число степеней свободы этой 3-фазной n-компонентной системы будет равно C=n–2.

Таким образом, состояние этой 3-фазной n-компонентной системы при постоянной температуре будет определяться n-2 параметрами. То есть, если задать n-2 концентрации компонентов в расплаве, то однозначно будет определяться состав расплава, шлака и газовой фазы.

Если в систему добавить новую фазу, например футеровку из оксида магния (присутствие оксида магния в чистом виде), то число уравнений, описывающих систему, увеличится на единицу, при этом число степеней свободы уменьшиться на единицу.

Эта термодинамическая система описывается следующей системой уравнений. Для каждого компонента шлака согласно закону действующих масс можно записать уравнение, например, для CaO:

(1)

где [O] — растворенный кислород; [Ca] — растворенный кальций; (CaO) — компонент шлака (оксид кальция).

Константа равновесия реакции (1) равна 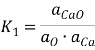, где K1 — константа равновесия; – активность оксида кальция в шлаке; — активность кислорода в расплаве; – активность кальция в расплаве.

Отсюда, активность оксида кальция в шлаке можно записать так:

(2)

Константа равновесия рассчитывается как алгебраическое произведение констант равновесия образования составляющих реакций из простых веществ.

Для реакции (1): 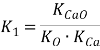, где KCaO — константа равновесия образования компонента шлака (CaO) из простых веществ; и — константы равновесия образования компонента раствора [O] и [Ca] из простых веществ.

Константа равновесия реакция определяется по формуле 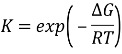, где ∆G=∆H-T∙∆S — стандартная энергия Гиббса; ∆H; ∆S — стандартная энтальпия и энтропия образование соединений из простых веществ. Эти величины определяются экспериментально и приведены в справочниках [1].

В качестве стандартного состояния для оксидов используется оксид в чистом виде, для растворов газов — газ при атмосферном давлении, а для раствора металла и углерода — чистый металл и углерод.

Таким образом, количество уравнений вида (2) будет равно числу составляющих шлака.

Недостающие два уравнения представляют собой уравнения материального баланса: сумма мольных долей составляющих в расплаве и шлаке равна единице.

Активность составляющих раствора определяется по формуле , где — активность кислорода в расплаве; — коэффициент активного кислорода в расплаве; CO — концентрация кислорода в расплаве, % по массе.

Коэффициент активности составляющей в растворе определяется по формуле, например, для кислорода 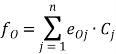, где eOj — коэффициент взаимодействия кислорода с j-ой компоновкой расплава; — концентрация j-ой составляющей расплава; j-ый — индекс компонента расплава (всего n компонентов).

Активность составляющих шлака, например, для CaO выражена следующей формулой , где — активность CaO в шлаке; — коэффициент активности CaO в шлаке; — концентрация CaO в шлаке.

Коэффициент активности составляющих шлака определяется по теории регулярных растворов. Этот коэффициент зависит от температуры и концентрации составляющих в шлаке.

Процесс десульфурации расплава рассчитывается согласно уравнению замещения кислорода в шлаке серой, например:

(3)

где [S] — растворенная сера; [O] — растворенный кислород; (CaO) и (CaS) — составляющие шлака.

Процесс дефосфорации описывается по реакции окисления фосфора и перехода оксида фосфора в шлак:

(4)

где [O] — растворенный кислород; [P] — растворенный фосфор; (P2O5) — составляющие шлака.

Активность сульфида кальция в шлаке согласно реакции (3) определяется уравнением 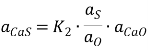, где K2 — константа равновесия реакции (3); — активность кислорода в расплаве; – активность сульфида кальция в шлаке; – активность серы в расплаве; – активность оксида кальция в шлаке.

Активность оксида фосфора в шлаке согласно реакции (4) определяется уравнением , где K3 — константа равновесия реакции (4); — активность оксида фосфора в шлаке; — активность фосфора в расплаве; — активность кислорода в расплаве.

Процесс раскисления стали добавками протекает по реакции вида:

(5)

Активность оксида алюминия в шлаке согласно реакции (5) определяется по формуле .

Давление составляющих в газовой фазе определяется из уравнений вида:

(6)

(7)

Согласно реакциям (6) и (7), давление CO и CO2 определяется по формулам соответственно , .

Реакции (6) и (7) описывают также процесс обезуглероживания расплава.

Алгоритм программы следующий:

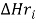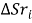1. задать энтальпию, энтропию образования и компонентов расплава из простых веществ, выбирается из справочных таблиц [2];
2. задать энтальпию и энтропию образования компонентов шлака из простых веществ;
3. вычислить стандартную энергию Гиббса ∆G и Kr константу равновесия образования компонентов расплава и шлака из простых веществ;
4. задать состав стали, и выбрать независимые составляющие, то есть компоненты;
5. задать необходимые уравнения взаимодействия составляющих между расплавом, шлаком и газовой фазой;
6. составить систему нелинейных алгебраических уравнений, описывающую заданную термодинамическую систему;
7. определить равновесный состав фаз, шлака, газовой фазы, а также степени рафинирования расплава от примесей кислорода, фосфора и т. д. Начальное состояние системы (то есть начальный состав расплава) определяется суммой равновесных концентраций компонентов во всех фазах.

Для примера рассмотрим процесс плавки стали состава С=0,18 О2=0,015 Al=0.05 S=0.015 Cr=2 Ni=4 Si=0.2 Mn=0.45 P=0.35.

На рис. 2 показана зависимость давления СО от температуры. Давление СО уменьшается с увеличением температуры и составляет несколько атмосфер при заданном составе. В этом случае газовая фаза предохраняет раствор от окисления.

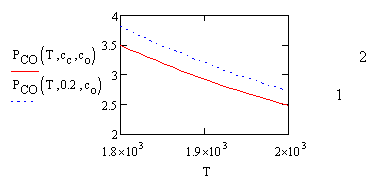
Рис. 2. Зависимость давления СО от температуры системы: 1 — Cс=0,1; 2 — СС =0,2, мас. %

На рис. 3 показана зависимость концентрации фосфора в расплаве от температуры. Процесс моделирование показывает, что дефосфорация стали улучшается при снижении температуры раствора и увеличении концентрации кислорода в расплаве.

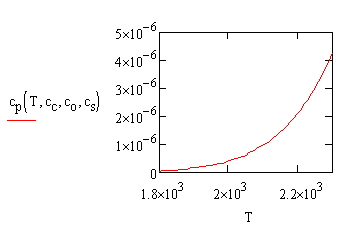
Рис. 3. Зависимость концентрации фосфора от температуры

На рис. 4 показана зависимость концентрации серы от концентрации кислорода в расплаве. Содержание серы уменьшается при увеличении температуры и снижении активности кислорода в растворе.

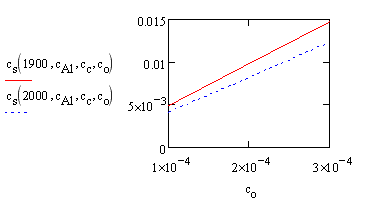
Рис. 4. Зависимость концентрации серы от концентрации кислорода: 1 — Т=1900К; 2 — Т=2000К

Предложенная модель и программа позволяет моделировать все равновесные процессы, протекающие при плавки стали любого состава, определять степень и механизмы очистки расплава от кислорода, серы, фосфора и других примесей, определять конечный состав шлака и неметаллических включений, задавать оптимальную последовательность процессов раскисления, дефосфорации, а также определять количество вносимых добавок для получения заданного конечного состава стали.

Литература:

1. Физико-химические расчеты элекстросталеплавильных процессов: Сб. задач с решениями / В. А. Григорян, А. Я. Стомахин, Ю. И. Уточкин и др. — 2-е изд., перераб. и доп. — М.: МИСиС, 2007. — 318 с.
2. Петелин А. Л. Термодинамика и кинетика металлургических процессов: курс лекций / А. Л. Петелин, Е. С. Михалина. — М.: Изд-во «Учеба», 2005. — 92 с.