Об оценке несущей способности бруса круглого поперечного сечения пористой структуры при поперечном изгибе
Авторы: Шляхов Станислав Михайлович, Гаврилов Данила Юрьевич
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
IV международная научная конференция «Актуальные вопросы технических наук» (Краснодар, февраль 2017)
Дата публикации: 27.01.2017
Статья просмотрена: 24 раза
Библиографическое описание:
Шляхов, С. М. Об оценке несущей способности бруса круглого поперечного сечения пористой структуры при поперечном изгибе / С. М. Шляхов, Д. Ю. Гаврилов. — Текст : непосредственный // Актуальные вопросы технических наук : материалы IV Междунар. науч. конф. (г. Краснодар, февраль 2017 г.). — Краснодар : Новация, 2017. — С. 60-62. — URL: https://moluch.ru/conf/tech/archive/229/11782/ (дата обращения: 24.04.2024).
Рассмотрим напряженно-деформированное состояние бруса круглого поперечного сечения пористой структуры при поперечном изгибе. При изгибе бруса под действием поперечной силы ![]() , в поперечном сечении возникают не только нормальные напряжения, но и касательные.
, в поперечном сечении возникают не только нормальные напряжения, но и касательные.
Известно, что упругая характеристика материала — касательные напряжения ![]() является функцией пористости материала [1], [2]. На основе экспериментальных данных для пористой стали, приведенных в таблице 1, зависимость
является функцией пористости материала [1], [2]. На основе экспериментальных данных для пористой стали, приведенных в таблице 1, зависимость ![]() может быть представлена полиномом
может быть представлена полиномом
Таблица 1
|
Пористость |
|
|
0 |
115,47 |
|
0,12 |
43,88 |
|
0,21 |
37,53 |
|
0,31 |
25,40 |
|
0,37 |
17,90 |
|
0,43 |
13,86 |
Сглаживая заданную функцию методом наименьших квадратов, коэффициенты ![]() найдем с помощью минимизации отклонения сглаживающей функции от заданных точек в некотором среднеинтегральном смысле.
найдем с помощью минимизации отклонения сглаживающей функции от заданных точек в некотором среднеинтегральном смысле.
![]() (1)
(1)
Конечным результатом МНК будут являться значения соответствия ![]() пористости в границах от 0 до 0,43.
пористости в границах от 0 до 0,43.
На рис.1 приведен график функции (1) при значениях коэффициентов (МПа), приведенных в табл.2. Точками обозначены экспериментальные значения упругих характеристик.
Таблица 2
|
|
109,87 |
|
|
-515,67 |
|
|
708,15 |
![]()
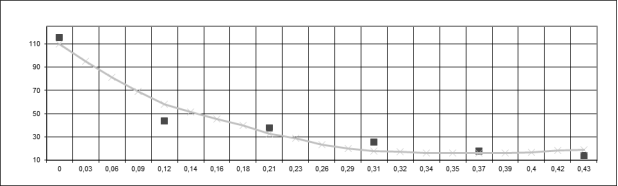
Рис.1
В качестве примера рассмотрим брус радиусом 0,2 м.
Для приближенного решения разобьем все сечения бруса по радиусу на «n» кольцевых элементов с наружными высотами ![]() , i=1,2,…,n с шагом
, i=1,2,…,n с шагом ![]() где r — радиус сечения бруса и «m» секторов с углом сектора
где r — радиус сечения бруса и «m» секторов с углом сектора ![]() ,
,![]() =1,2,3,...,m с шагом
=1,2,3,...,m с шагом ![]() .
.
Распределение пористости по поперечному сечению определено исходя из предельных нормальных напряжений и представлены на рис. 2
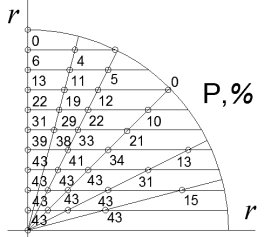
Рис. 2
Касательные напряжений в каждом элементе найдем по (1).
Эпюра распределения касательных напряжений представлена на рис. 3
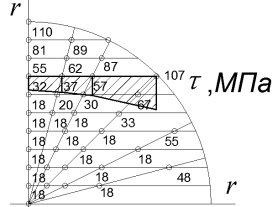
Рис. 3
Как известно,
Производя вычисления по (2), получаем, что суммарная поперечная сила Q, воспринимаемая брусом с рационально распределенной по сечению пористостью равна 1,590 кН, средняя пористость в сечении 29 %.
При распределении пористости по квадратной параболе 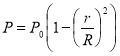 суммарная перерезывающая сила равна 1,493 кН, что на 6,1 % ниже, чем при рационально подобранной пористости.
суммарная перерезывающая сила равна 1,493 кН, что на 6,1 % ниже, чем при рационально подобранной пористости.
При средней пористости Q=0,654кН, что на 59 % ниже, чем при рационально подобранной пористости.
Таким образом, при рациональном подборе пористости подтверждено повышение несущей способности бруса круглого поперечного сечения при изгибе.
Литература:
- Кашталян Ю. А. Характеристики упругих материалов при высоких температурах. /Ю. А. Кашталян. Киев. Наукова думка, 1970. 112с.
- Белов С. В. Пористые металлы в машиностроении. / С. В. Белов. Москва. Машиностроение, 1981. 247с.
Похожие статьи
Геофизические методы определения пористости
Геофизические методы определения пористости. Автор: Абубакирова Зилия Вилевна. Рубрика: Геология.
Диффузионная длина убывает с увеличением водородосодержания и содержания в породах элементов с аномально высокими ядерными сечениями захвата.
Закономерности формирования структуры пеноминеральных...
где (1- eпор) — доля поперечного сечения, занятого каналами Плато.
Выразив средний радиус воздушной ячейки через общую пористость материала Vпор и количество пор N, получаем зависимость вида
Анализ методов определения сжимаемости | Статья в журнале...
Колебания двух поляризованных поперечных волн ориентированы друг к другу под углом 900.
Рис. 1. Распределение плотности насыщенных образцов и коэффициента пористости образцов по глубине залегания.
Разработка пористого железа из шлака на основе вспенивания...
Рис. 2. А. Изменение температуры шлака и пористости вспененного образца от времени выдержки.
На рисунке 2Б приведена макроструктура поперечного сечения вспененного шлака, нагретого до 1400°С, при времени выдержки 40с, 100с и 150с соответственно.
Оценка вторичной пористости карбонатных коллекторов...
В данной статье рассмотрены возможности геофизических методов для определения вторичной пористости карбонатных коллекторов сложного строения, вскрываемых на больших глубинах, на примере газоконденсатного месторождения Жанажол.
Линейные колебания упругого криволинейного стержня
Продольно-поперечный изгиб стержней переменного поперечного сечения. О распространении гармонических волн в деформируемой...
Для решения поставленной задачи рассмотрим движение вязкой жидкости при учете расхода через пористости стенок и.
Литология, петрофизическая и промыслово-геофизическая...
Их открытая пористость порядка 7,5 %, газопроницаемость 0,5 мд. При опробовании скв. 9 пластоиспытателем (инт.
Несмотря на ограниченность керновых данных и неравномерное их распределение по разрезу и площади, анализ изменения емкостно-фильтрационных свойств...
Метод сквозного счета для численного моделирования...
покрытием полимерного пористого материала с открытыми ячейками частицами металлического сплава методом
Вычисления выполняются для моделирования деформации блока пористого алюминия с различными значениями пористости (5 %, 10 %, 25 %).
Похожие статьи
Геофизические методы определения пористости
Геофизические методы определения пористости. Автор: Абубакирова Зилия Вилевна. Рубрика: Геология.
Диффузионная длина убывает с увеличением водородосодержания и содержания в породах элементов с аномально высокими ядерными сечениями захвата.
Закономерности формирования структуры пеноминеральных...
где (1- eпор) — доля поперечного сечения, занятого каналами Плато.
Выразив средний радиус воздушной ячейки через общую пористость материала Vпор и количество пор N, получаем зависимость вида
Анализ методов определения сжимаемости | Статья в журнале...
Колебания двух поляризованных поперечных волн ориентированы друг к другу под углом 900.
Рис. 1. Распределение плотности насыщенных образцов и коэффициента пористости образцов по глубине залегания.
Разработка пористого железа из шлака на основе вспенивания...
Рис. 2. А. Изменение температуры шлака и пористости вспененного образца от времени выдержки.
На рисунке 2Б приведена макроструктура поперечного сечения вспененного шлака, нагретого до 1400°С, при времени выдержки 40с, 100с и 150с соответственно.
Оценка вторичной пористости карбонатных коллекторов...
В данной статье рассмотрены возможности геофизических методов для определения вторичной пористости карбонатных коллекторов сложного строения, вскрываемых на больших глубинах, на примере газоконденсатного месторождения Жанажол.
Линейные колебания упругого криволинейного стержня
Продольно-поперечный изгиб стержней переменного поперечного сечения. О распространении гармонических волн в деформируемой...
Для решения поставленной задачи рассмотрим движение вязкой жидкости при учете расхода через пористости стенок и.
Литология, петрофизическая и промыслово-геофизическая...
Их открытая пористость порядка 7,5 %, газопроницаемость 0,5 мд. При опробовании скв. 9 пластоиспытателем (инт.
Несмотря на ограниченность керновых данных и неравномерное их распределение по разрезу и площади, анализ изменения емкостно-фильтрационных свойств...
Метод сквозного счета для численного моделирования...
покрытием полимерного пористого материала с открытыми ячейками частицами металлического сплава методом
Вычисления выполняются для моделирования деформации блока пористого алюминия с различными значениями пористости (5 %, 10 %, 25 %).











