В современном промышленном производстве широко применяется нагрев заготовок из черных и цветных металлов перед различными операциями пластической деформации: прокаткой, прессованием, штамповкой, волочением. В этих целях используют индукционно нагревательные установки (ИНУ) различных принципов действия и самого разнообразного конструктивного исполнения.
П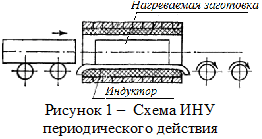 ри
малой производительности и сравнительно большой длине заготовки часто
используют ИНУ периодического действия. В периодических нагревателях
одно или несколько изделий нагревается до требуемой температуры,
после чего загрузка индуктора полностью заменяется (рис. 1).
ри
малой производительности и сравнительно большой длине заготовки часто
используют ИНУ периодического действия. В периодических нагревателях
одно или несколько изделий нагревается до требуемой температуры,
после чего загрузка индуктора полностью заменяется (рис. 1).
Индукционные нагревательные установки периодического действия являются сложными техническими объектами, в которых протекают физические процессы электромагнитной и тепловой природы. В общем случае математическое описание таких объектов представляет собой систему детерминированных нелинейных дифференциальных и интегральных уравнений, записанных для многомерных и многосвязных областей. Если не вводить существенных упрощений в постановку задачи, то решение указанной системы уравнений, следовательно, и количественное описание изучаемого объекта может быть получено только численными методами [1,2]. К настоящему времени наибольшее распространение при решении дифференциальных уравнений получили численные методы конечных разностей (МКР) и конечных элементов (МКЭ) [3].
Современные технологии конечно-элементного анализа реализуются в программных пакетах высокого уровня. Одним из специализированных программных продуктов, предназначенных для многопараметрического электромагнитного, теплового и электромеханического анализа, является пакет FLUX, разработанный французской компанией Cedrat [4].
Перечислим основные этапы численного моделирования процесса индукционного нагрева металла на базе программного пакета FLUX: задание исходных данных в предпроцессор, численное решение в процессоре, обработка результатов в постпроцессоре.
Для ИНУ, представленной на рисунке 1, необходимые исходные данные приведены в таблице.
Исходные данные для численного моделирования ИНУ
|
Длина индуктора, м |
1,046 |
|
Заданная температура заготовки, 0С |
1200 |
|
Температура окружающей среды, 0С |
20 |
|
Начальная температура заготовки, 0С |
20 |
|
Частота питающего тока, Гц |
2300 |
|
Число витков |
42 |
|
Внутренний диаметр катушки индуктора, мм |
145 |
|
Геометрические параметры витка, мм |
15 х 20 |
|
Расстояние между витками, мм |
4 |
|
Диаметр заготовки, мм |
105 |
|
Материал заготовки, сталь |
С 40 |
|
Напряжение источника питания, В |
450 |
|
Время нагрева, с |
509 |
Работа в предпроцессоре программного пакета FLUX
Н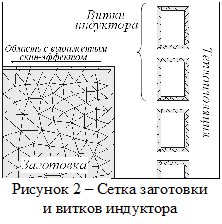 а
первом этапе моделирования осуществляется построение геометрии,
генерация сетки и задание физических свойств в окне предпроцессора
FLUX.
Перед тем как начать создавать единичные геометрические объекты
(точки, линии), следует задать оси симметрии. Процесс построения
значительно упростится и ускорится, если придется строить ½
или, как в нашем случае ¼ часть от всей модели, поскольку
рассматриваемая ИНУ симметрична относительно обеих осей.
а
первом этапе моделирования осуществляется построение геометрии,
генерация сетки и задание физических свойств в окне предпроцессора
FLUX.
Перед тем как начать создавать единичные геометрические объекты
(точки, линии), следует задать оси симметрии. Процесс построения
значительно упростится и ускорится, если придется строить ½
или, как в нашем случае ¼ часть от всей модели, поскольку
рассматриваемая ИНУ симметрична относительно обеих осей.
При построении модели используются единичные геометрические объекты. Сначала задаются точки, с соответствующими координатами, затем точки соединяются линиями, образуя поверхности. Заканчивается построение геометрии заданием конечной области, ограничивающей окружающее пространство.
После задания геометрических параметров заготовки, индуктора и окружающего пространства переходим к построению сетки.
При построении сетки окружающего пространства наибольший интерес представляет то, как ведет себя электромагнитное поле в непосредственной близости к заготовке и виткам индуктора, в этом месте плотность разбиения будет максимальной. Плотность сетки становится тем меньше, чем дальше она от основных элементов модели.
П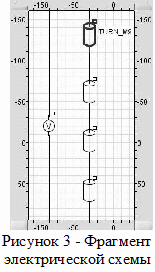 ри
разбиении заготовки следует учесть
скин-эффект, для этого на ее поверхности задается специальная
область, имеющая соответствующие геометрические параметры (рис. 2). В
результате описанных операций была сгенерирована сетка, состоящая из
3-х угольных элементов и лишь в области, где наиболее выражен
скин-эффект, используются 4-х угольные элементы.
ри
разбиении заготовки следует учесть
скин-эффект, для этого на ее поверхности задается специальная
область, имеющая соответствующие геометрические параметры (рис. 2). В
результате описанных операций была сгенерирована сетка, состоящая из
3-х угольных элементов и лишь в области, где наиболее выражен
скин-эффект, используются 4-х угольные элементы.
Прежде чем приступить к описанию основных электромагнитных, теплофизических свойств материалов и заданию граничных условий следует выбрать тип задачи (модуль). Рассмотрим модуль, решающий совместно электромагнитную и тепловую задачи (электромагнитный – тепловой). За основу в нем берутся установившиеся электромагнитные и переходные тепловые процессы.
Конструкцию модели можно разбить на 25 частей, каждая из которых имеет свои электромагнитные и тепловые свойства: заготовка, 21 виток катушки, теплоизоляция, охлаждающая вода, окружающее пространство.
Для задания свойств воздуха, воды и меди была использована стандартная библиотека материалов. В пакете FLUX так же существует возможность создания новых материалов, если все их необходимые электромагнитные, теплофизические свойства известны.
Особенностью пакета FLUX является возможность создания электрических схем. На рисунке 3 представлен фрагмент электрической схемы, которая соответствует моделируемой ИНУ.
Для того чтобы физическое описание модели было полным, необходимо задать граничные условия для тепловой задачи. Всей поверхности заготовки присваивается имя CON_RAD и в соответствующем диалоговом окне прописываются свойства, задаются коэффициенты лучистого и конвективного теплообмена.
Численное решение поставленной задачи в процессоре FLUX
После того, как работа с предпроцессором FLUX завершена, новый проект сохраняется, при этом автоматически создаются файлы с расширением INDHEAT.FLU, INDHEAT.TRA, INDHEAT.CID. Первый файл содержит всю информацию о геометрии, сетке, физических свойствах модели. Он запускается препроцессором для того, чтобы изменять, модифицировать разработанную модель. Второй файл необходим для дальнейшего численного решения. В третьем файле сохраняется вся информация об электрических схемах.
При запуске решателя считывается файл INDHEAT.TRA, в котором содержатся все данные по модели. Для того чтобы расчет был запущен, необходимо задать временной шаг, время расчета, количество шагов, начальную температуру и температуру окружающей среды.
Обработка результатов в постпроцессоре программного пакета FLUX
Р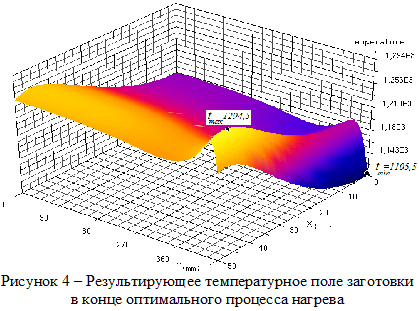 езультатом
работы решателя FLUX является два файла с именами INDHEAT_M.TRA,
INDHEAT_T.TRA, они создаются автоматически и предназначены для
дальнейшей обработки в постпроцессоре.
езультатом
работы решателя FLUX является два файла с именами INDHEAT_M.TRA,
INDHEAT_T.TRA, они создаются автоматически и предназначены для
дальнейшей обработки в постпроцессоре.
Первый файл содержит всю информацию о поведении магнитного поля, об изменении в течение времени электромагнитных свойств материалов.
Д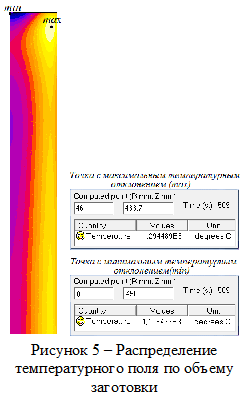 анные
о поведении поля температур и об изменении в течение времени
теплофизических свойств материалов содержит файл INDHEAT_T.TRA.
Используя широкий круг возможностей постпроцессора FLUX, можно
проанализировать пространственно-временное распределение температуры
по объему заготовки, применяя различные форматы файлов выхода.
анные
о поведении поля температур и об изменении в течение времени
теплофизических свойств материалов содержит файл INDHEAT_T.TRA.
Используя широкий круг возможностей постпроцессора FLUX, можно
проанализировать пространственно-временное распределение температуры
по объему заготовки, применяя различные форматы файлов выхода.
Работа на этом этапе представляет наибольший интерес, так как основной целью нагрева заготовки в ИНУ является обеспечение с определенной точностью равномерного распределение температур по всему ее объему (рис. 4).
На рисунке 5 видно, как располагаются по объему цилиндрической заготовки точки с максимальными отклонениями от заданной температуры (1200 0С) в конце оптимального процесса нагрева.
Максимальная температура (1294,4 0С) создается не на поверхности тела, а на некоторой глубине, в зоне источников теплоты (в нашем случае это точка с координатами (46;433,7)). Это следует из того, что при моделировании был учтен лучистый и конвективный теплообмен с поверхности заготовки. По этой же причине на оси в точке координатами (0;450) находится ярко выраженный глобальный минимум, значение температуры в котором 1105,5 0С. Большое влияние на температурное распределение оказывают концевые эффекты, по этой причине точка с максимальной температурой находится не в центре заготовки, а ближе к краю.
Как видно из рисунка 4, отклонение результирующего температурного поля по всему объему заготовки в конце оптимального процесса нагрева не превышает 94,5 0С.
Заключение
На базе конечно-элементного программного пакета FLUX была разработана численная двумерная модель индукционной нагревательной установки периодического действия. При моделировании рассматриваемого процесса были учтены следующие факторы: зависимость теплофизических свойств материала заготовки от температуры и от неравномерности магнитного поля; все способы теплопередачи; совместное решение электромагнитной и тепловой задач.
Разработанная двумерная модель позволяет выявлять основные физические закономерности поведения температурных полей и анализировать распределение температуры по всему объему заготовки. Данная модель может быть использована в оптимизационных процедурах для решения задач оптимального управления многомерными температурными полями в процессе периодического индукционного нагрева.
Литература:
- Немков В.С., Демидович В.Б. Теория и расчет устройств индукционного нагрева. – Л.: Энергоатомиздат, 1988. – 280 с.
- Установки индукционного нагрева / Слухоцкий А.Е., Немков В.С., Павлов Н.А., Бамунер А.В. – Л.: Энергоатомиздат, 1981. – 328 с.
- Rapoport E., Pleshivtseva Yu. Optimal Control of Induction Heating Processes. CRC Press, Taylor & Francis Group, Roca Ration, London, New York, 2007. – 360 с.
- http://www.cedrat.com

