Реализация многослойного персептрона и сети адаптивного резонанса



Реализация многослойного персептрона и сети адаптивного резонанса

Быканов Никита Павлович, студент

Балтийский государственный технический университет «Военмех» имени Д. Ф. Устинова

Нейронные сети, называемые персептронами (от лат. perceptio — восприятие), представляют математическую модель процесса восприятия образов. Эта модель реализуется в виде слоев нейронов: рецепторного слоя и одного или нескольких слоев преобразующих нейронов [1, c.56]. Под обучением многослойного персептрона понимается процесс адаптации сети к предъявленным эталонным образцам путем модификации весовых коэффициентов связей между нейронами.

Сеть обучается методом обратного распространения ошибки. Обучение многослойного персептрона методом обратного распространения ошибки предполагает два прохода по всем слоям сети: прямой и обратный. При прямом проходе образ (входной вектор) подается на сенсорные узлы сети, после чего распространяется от слоя к слою. В результате генерируется набор выходных сигналов, который и является фактической реакцией сети на данный входной образ. Во время прямого прохода все синаптические веса сети фиксированы. Во время обратного прохода они настраиваются в соответствии с правилом коррекции ошибок, а именно: фактический выход сети вычитается из желаемого отклика, в результате чего формируется сигнал ошибки. Этот сигнал впоследствии распространяется по сети в направлении, обратном направлению синаптических связей. Отсюда и название «алгоритм обратного распространения ошибки».

Для обучения нейронной сети c помощью персептрона выбираются четыре образца из предлагаемых изображений. Образцы для обучения сети представлены на рисунке 1.

Рис. 1. Образцы рисунков для обучения сети

В процессе обучения производится тестирование обобщающих свойств сети. Для этого формируется тестовая выборка из восьми образцов. В качестве тестовых образцов используются условно «искаженные» обучающие образцы. Для этого из каждого обучающего образца формируются два условно «поцарапанных» образца — в них часть точек не «белого» цвета заменяется на «белый». Для тестовых образцов вычисляется ошибка на выходе сети, но она не используется для корректировки весовых коэффициентов.

На рисунках 2 и 3 представлены результаты выполнения программы в момент обучения и в момент расчета.

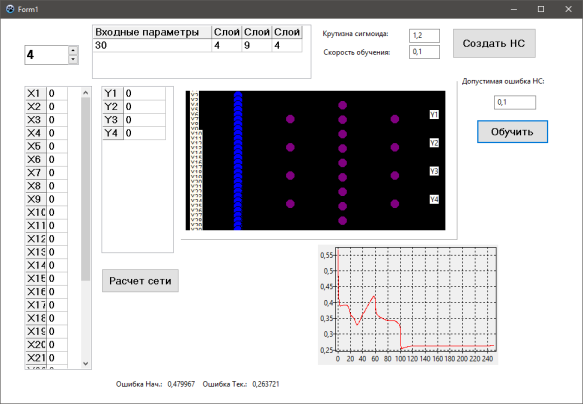
Рис. 2. Обучение сети

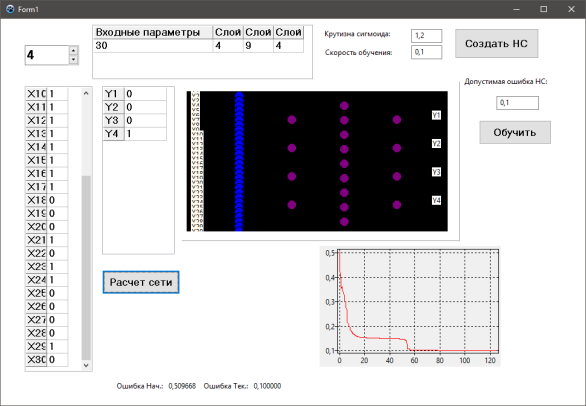
Рис. 3. Расчет сети

Сети адаптивного резонанса — разновидность искусственных нейронных сетей основанная на теории адаптивного резонанса Стивена Гроссберга и Гейла Карпентера [2, c.35].

В сетях адаптивной резонансной теории (АРТ) предпринимается попытка приблизить механизм запоминания образов в ИНС к биологическому. Результатом работы АРТ является устойчивый набор запомненных образов и возможность выборки «похожего» образа по произвольному вектору, предъявленному на вход сети. Важное качество АРТ динамическое запоминание новых образов без полного переобучения и отсутствие потерь уже запомненных образов при предъявлении новых.

В процессе классификации образов можно выделить пять основных фаз: инициализацию, распознавание, сравнение, поиск и обучение.

Инициализация. Перед началом процесса обучения сети АРТ все весовые векторы несвязанных нейронов, а также параметр сходства должны быть установлены в начальные значения. Всем весам векторов присваиваются одинаковые малые значения.

Распознавание. В начальный момент времени вектор X отсутствует на входе сети. Следовательно, все компоненты входного вектора X можно рассматривать как нулевые: xi = 0.Затем на вход слоя сравнения подается вектор X, который должен быть классифицирован.

Сравнение.В слое сравнения веер сигналов отклика слоя распознавания сравнивается с компонентами вектора X. Выход слоя сравнения C теперь содержит единичные компоненты только в тех позициях, в которых единицы имеются и у входного вектора X и у вектора обратной связи P. Если в результате сравнения векторов C и X не будет обнаружено значительных отличий, то нейрон сброса остается неактивным. Вектор C вновь вызовет возбуждение того же нейрона-победителя в слое распознавания, что и удачно завершит процесс классификации. В противном случае будет выработан сигнал сброса, который начнет фазу поиска.

Поиск. Если значение параметра сходства выигравшего нейрона превышает пороговый уровень, поиск не требуется, процесс классификации на этом завершается. В противном случае другие запомненные образы должны быть исследованы с целью поиска лучшего соответствия.

Обучение. Обучающий алгоритм используется в случае как успешного, так и неуспешного поиска. Вектору весов возбужденного нейрона в распознающем слое присваиваются новые значения.

Для реализации сети АРТ-1 рассмотрим набор примеров для обучения из 5 образцов.

Каждый образец — это символ, состоящий из 12 точек (матрица 4х3).

Точка может быть белой (Хi = 0) или черной (Хi = 1). Пример образца представлен на рисунке 4.

Рис. 4. Пример для обучения сети АРТ

Кодировка образца: 0100 0110 1101

Образцы последовательно подаются на вход сети. Параметр — «порог сходства» по умолчанию: 0.8 (предусмотреть возможность его изменения).

Алгоритм реализации:

1. Определить количество обученных нейронов в слое распознавания.
2. Определить весовые коэффициенты Bj и Tj обученных нейронов.
3. Показать образцы, запомненные обученными нейронами.

Реализация сети АРТ-1 представлена на рисунке 5.

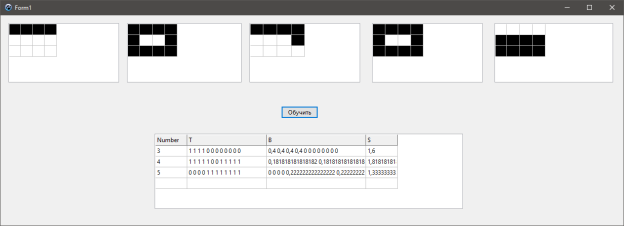
Рис. 5. Обучение сети АРТ

Типовые задачи, решаемые в контексте ИНС и представляющие научный и практический интерес, можно подразделить следующим образом:

1. Классификация образов. Задача состоит в указании принадлежности входного образа (например, речевого сигнала или рукописного символа), представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови [2, c.77].
2. Кластеризация/категоризация. При решении задачи кластеризации, которая известна также как классификация образов «без учителя», отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Кластеризация применяется для извлечения знаний, сжатия данных и исследования их свойств.

Таким образом, с помощью многослойного персептрона, используя алгоритм обратного распространения ошибки, можно решать задачи классификации, а при решении задач кластеризации можно использовать сети адаптивной резонансной теории.

Литература:

1. Головко В. А., под ред. проф. А. И. Галушкина Нейронные сети: обучение, организация и применение. — Москва: ИПРЖР, 2001 г. — 230 с.
2. Толмачев С. Г., Системы искусственного интеллекта. Нейросетевые модели: учебное пособие, Балт. гос. техн. ун-т. — СПб., 2011 г. — 170 с.