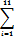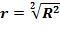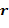Процесс транспортировки продукта неотъемлемо связан с его потребностью. Процесс транспортировки продукта является нелинейным, так как известно, что потребность продукта может изменяться в зависимости от различных внешних факторов, например, сезонности потребления (зависимости потребления продукта от времени суток, дня недели, времени года). Также на нелинейность процесса транспортировки продукта могут влиять ряд других факторов, зависящих от вида продукта и технологических особенностей производственного процесса предприятия [1].
На основании полученных аутентичных данных от предприятия по транспортировке продукта приведем сводную таблицу зависимости потребности продукта Q от условного аргумента t, принимающего целые значения на конкретный сезон S.
Таблица 1
Зависимость потребления продукта
|
n |
Условный аргумент, t |
Фактическая потребность продукта, Qф ед. изм. |
|
1 |
-11 |
1315,0 |
|
2 |
-11 |
1316,0 |
|
3 |
-11 |
1325,0 |
|
4 |
-7 |
1157,0 |
|
5 |
-9 |
1256,0 |
|
6 |
-7 |
1177,0 |
|
7 |
-11 |
1324,0 |
|
8 |
-12 |
1345,0 |
|
9 |
-5 |
1074,0 |
|
10 |
-4 |
940,0 |
|
11 |
-2 |
925,0 |
|
12 |
-2 |
918,0 |
|
13 |
1 |
857,0 |
|
14 |
0 |
892,0 |
|
15 |
0 |
890,0 |
|
16 |
-2 |
904,0 |
|
17 |
2 |
870,0 |
|
18 |
0 |
879,0 |
|
19 |
-2 |
900,0 |
|
20 |
0 |
886,0 |
|
21 |
0 |
891,0 |
|
22 |
1 |
850,0 |
|
23 |
0 |
886,0 |
|
24 |
0 |
873,0 |
|
25 |
-3 |
922,0 |
|
26 |
-6 |
1105,0 |
|
27 |
-5 |
1058,0 |
|
28 |
-6 |
1107,0 |
|
29 |
-7 |
1143,0 |
|
30 |
-7 |
1173,0 |
|
31 |
-4 |
950,0 |
где t — условный аргумент, принимающий целые значения; Qф — фактическая потребность продукта.
Приведем систему уравнений, описывающую зависимость изменения потребности продукта от условного аргумента для конкретного сезона (времени года) (S=const). Для основных потребителей приняты следующие интервалы значений условного аргумента: -¥; -10; -5; -2,5; 0; +2,5; +10; +¥. Значения S=const позволяют исключить влияние сезонной неравномерности потребления продукта. Нелинейную зависимость потребности продукта от условного аргумента t на определенный сезон S представим в виде следующей кусочно-линейной модели:
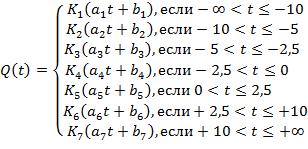 , (1)
, (1)
где ai, bi (i=1,...,7) — коэффициенты регрессионного уравнения [2], сохраняющие постоянные значения внутри интервалов значений условного аргумента; Ki (i=1,...,7) — коэффициент адаптивный.
Представленную кусочно-линейную модель (1) предлагается использовать для прогнозирования потребности продукта. Введенный коэффициент адаптации Ki позволяет адаптировать кусочно-линейную модель для случаев скачкообразного изменения потребности продукта, носящих кратковременный или постоянный характер, что, в свою очередь, значительно повышает точность прогноза.
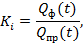 (2)
(2)
Необходимость адаптации кусочно-линейной модели путем пересчета коэффициента Kiопределяется путем задания значения допустимого отклонения прогнозируемой величины от фактической (3).
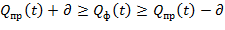 , (3)
, (3)
где 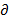 — допустимое отклонение прогнозируемой величины потребности продукта от фактической.
— допустимое отклонение прогнозируемой величины потребности продукта от фактической.
Пересчет коэффициента Ki целесообразно проводить в случае, когда изменение носит кратковременный характер, при котором нет необходимости пересчета коэффициентов регрессионного уравнения.
В связи с корректным выбором интервалов условного аргумента, тренд, описывающий изменение расхода продукта от условного аргумента на каждом интервале, оказался практически линейным или с незначительными отклонениями от линейности. В [3, 4] показано, что в данном случае наиболее надежным способом построения линейных уравнений кусочно-линейной модели (1) будет метод наименьших квадратов.
Для нахождения коэффициентов ai, bi (i=1,...,7) достаточно воспользоваться системой формул [5].
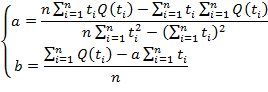 (4)
(4)
Воспользовавшись системой уравнений (4) по данным из таблицы 1, рассчитаем коэффициенты регрессионных уравнений на примере интервала условного аргумента от -2,5 до 0 °С.
Для удобства вычисления сумм, которые входят в формулы искомых коэффициентов, заполним таблицу.
Таблица 2
Вспомогательнаятаблица
|
|
i=1 |
i=2 |
i=3 |
i=4 |
i=5 |
i=6 |
i=7 |
i=8 |
i=9 |
i=10 |
i=11 |
|
|
ti |
-2 |
-2 |
0 |
0 |
-2 |
0 |
-2 |
0 |
0 |
0 |
0 |
-8 |
|
Qi (ti) |
925 |
918 |
892 |
890 |
904 |
879 |
900 |
886 |
891 |
886 |
873 |
9844 |
|
ti*Qi (t) |
-1850 |
-1836 |
0 |
0 |
-1808 |
0 |
-1800 |
0 |
0 |
0 |
0 |
-7294 |
|
t2i |
4 |
4 |
0 |
0 |
4 |
0 |
4 |
0 |
0 |
0 |
0 |
16 |
Подставляем значения из таблицы в систему уравнения (4) для нахождения коэффициентов регрессионного уравнения:
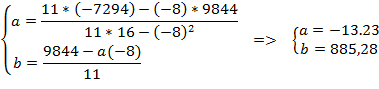
Регрессионное уравнение для интервала значений условного аргумента от -2,5 до 0 принимает вид:
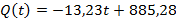
Проведя аналогичный расчет для других интервалов значений условного аргумента, данные которых присутствуют в таблице 1, получим значения коэффициентов регрессионных уравнений. Подставив значения полученных коэффициентов в уравнение (1), кусочно-линейная модель зависимости потребления продукта от условного аргумента примет следующий вид:
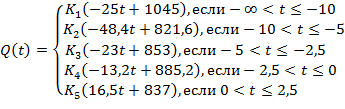 (5)
(5)
Алгоритм прогнозирования значений объема транспортируемого продукта комплексом по распределению с использованием описанной выше кусочно-линейной модели приведен на рисунке 1.
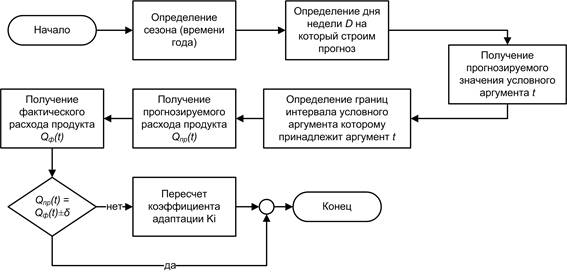
Рис. 1. Алгоритм прогнозирования объема транспортируемого продукта
Получив прогнозируемое значение условного аргумента t на конкретный день D сезона S, на который строим прогноз, определяем интервал условного аргумента, которому он принадлежит. Из кусочно-линейной модели выбираем уравнение, описывающее зависимость потребности продукта от условного аргумента для выбранного интервала. По уравнению рассчитываем прогнозируемую потребность продукта Qпр(t). При наступлении дня D получаем фактическое значение потребности продукта Qф(t). Если фактическое значение потребности продукта Qф, превышающее установленное допустимое отклонение δ, определено диспетчером как достоверное, то при необходимости производим адаптацию кусочно-линейной модели. Адаптация кусочно-линейной модели осуществляется путем автоматического пересчета коэффициента адаптации Ki (2).
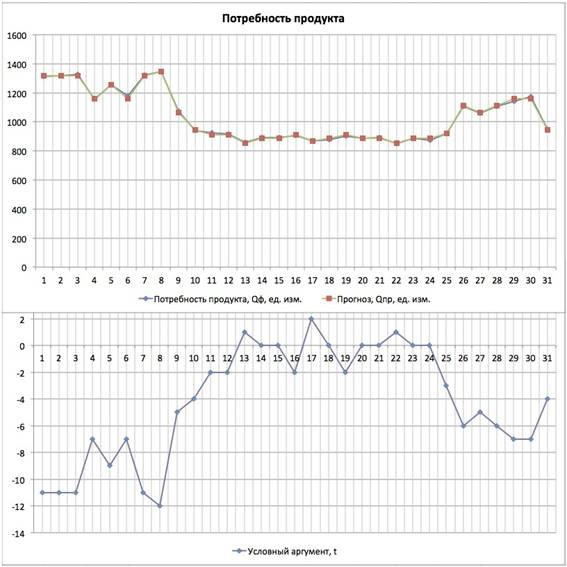
Рис. 2. Прогнозирование потребности продукта
Для оценки коэффициента адаптации K кусочно-линейной модели по прогнозированию потребности продукта (рисунок 1), смоделируем скачкообразное изменение потребности продукта (рисунок 2). Скачкообразное изменение позволит определить количество шагов, необходимых для адаптации алгоритма.
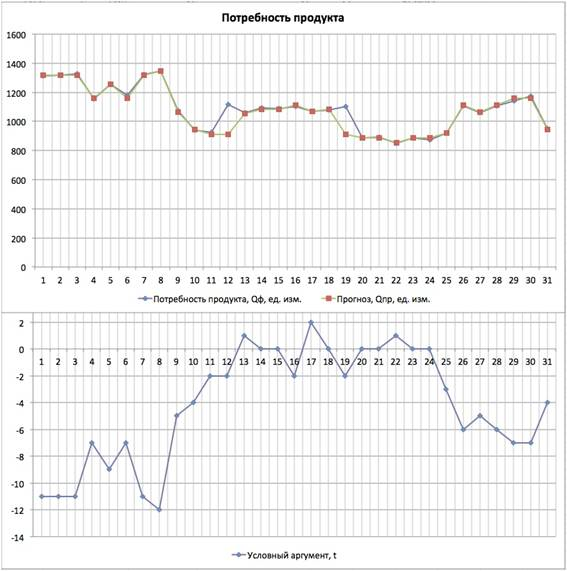
Рис. 3. Прогнозирование потребности продукта, адаптация модели
Из рисунка 3 видно, что предложенный алгоритм производит адаптацию кусочно-линейной модели уже на следующем шаге после возникновения смоделированного скачка, и, при получении следующего значения расхода продукта, сохраняет точность прогнозирования.
Помимо повышения точности прогнозирования, введение коэффициента адаптации Ki позволяет сократить количество пересчетов коэффициентов регрессионных уравнений ai, bi (i=1,...,7) кусочно-линейной модели (1). Сокращение количества пересчетов значительно экономит время, затрачиваемое на обработку данных.
Проверка достоверности кусочно-линейной модели.
По данным из таблицы 1 и данными, рассчитанными из кусочно-линейной модели (1), получим, что предельное отклонение прогнозируемой величины от фактической не превышает 1,52 %, а количество прогнозируемых величин с ошибкой менее 1 % составляет более 80 % от всех значений. Полученные результаты удовлетворяют требованиям технологического процесса транспортировки и распределения продукта, что позволяет констатировать о допустимой достоверности предложенной кусочно-линейной модели (1).
Однако, данного заключения не достаточно для оценки достоверности кусочно-линейной модели. Произведем расчет коэффициента детерминации для каждого температурного интервала, участвующего в опыте (таблица 3).
Коэффициент детерминации (R2) — это квадрат множественного коэффициента корреляции. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных [6].
Формула для вычисления коэффициента детерминации [6, 7]:
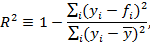 (6)
(6)
где yi — наблюдаемое значение зависимой переменной; fi — значение зависимой переменной по уравнению регрессии; 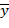 — среднее арифметическое зависимой переменной.
— среднее арифметическое зависимой переменной.
Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными. Коэффициент принимает значения из интервала [0;1]. Чем ближе значение к 1, тем ближе модель к эмпирическим наблюдениям. В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть  [6].
[6].
Использую шкалу Чеддока [8], дадим качественную оценку близости кусочно-линейной модели прогнозирования потребности продукта к эмпирическим наблюдениям (таблица 3).
Таблица 3
Расчетные значение коэффициентов детерминации
|
Температурный интервал |
Коэффициент корреляции Пирсона,
|
Шкала Чеддока | |
|
Количественная мера тесноты связи, |
Качественная характеристика силы связи | ||
|
-∞ < t ≤ -10 |
0,92 |
от 0,9 до 0,99 |
Весьма высокая |
|
-10 < t ≤ -5 |
0,97 |
от 0,9 до 0,99 |
Весьма высокая |
|
-5 < t ≤ -2,5 |
0,93 |
от 0,9 до 0,99 |
Весьма высокая |
|
-2,5 < t ≤ 0 |
0,84 |
от 0,7 до 0,9 |
Высокая |
|
0 < t ≤ +2,5 |
0,93 |
от 0,9 до 0,99 |
Весьма высокая |
Заметим, что функциональная связь обозначается 1, а отсутствие связи обозначается 0. При обозначениях показателей тесноты связи, превышающих 0,7, зависимость результативного признака Qпр(t) от факторного t является высокой, а при значении более 0,9 — весьма высокой. Это в соответствии с показаниями индекса детерминации R2 означает, что более половины общей вариации результативного признака Qпр(t) объясняется влиянием изучаемого фактора t. Последнее позволяет считать оправданным применение метода регрессионного анализа для получения корреляционной связи, а синтезированная при этом математическая модель (1) признается пригодной для практического использования. Предложенный алгоритм прогнозирования объема транспортируемого продукта совместно с введенным коэффициентом адаптации позволяет значительно увеличить точность прогнозирования для случаев, когда изменение носит кратковременный характер, при котором нет необходимости пересчета коэффициентов регрессионного уравнения.
Литература:
1. Сухарев, М. Г. Оптимизация систем транспорта газа / М. Г. Сухарев, Е. Р. Ставровский. − М.: Недра, 1975. − 277 с.
2. Корн, Г. Справочник по математике (для научных работников и инженеров) / Г. Корн, Т. Корн. − М.: Наука, 1977. − 832 с.
3. Брандт, З. Статистические методы анализа наблюдений / З. Брандт - М.: Мир, 1975. - 312 с.
4. Парная линейная регрессия. Метод наименьших квадратов [Электронный ресурс]. Режим доступа: http://studopedia.net/9_109190_tema--parnaya-lineynaya-regressiya-metod-naimenshih-kvadratov.html (дата обращения: 27.06.2015.05.2012).
5. Шор, Я. Б. Статистические методы анализа и контроля качества и надежности / Я. Б. Шор − М.: Советское радио, 1962. − 552 с.
6. Коэффициент детерминации [Электронный ресурс]. Режим доступа: http://ru.vlab.wikia.com/wiki/Коэффициент_детерминации (дата обращения: 27.06.2015).
7. Елисеева, И. И. Общая теория статистики: Учебник / под ред. чл.-корр. РАН И. И. Елисеевой / И. И. Елисеева, М. М. Юзбашев — 4-изд., перераб. и доп, — М.: Финансы и статистика, 2001. — 480 с.
8. Елисеева, И. И. Эконометрика: учебник / И. И. Елисеева [и др.]; под ред. И. И. Елисеевой. − 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2007. − 576 с.