В работе представлена модель композитного баллона давления изготавливаемого непрерывной жгутовой намоткой в виде системы дифференциальных уравнений, удобная для численного анализа, позволяющая получить конструкцию, образованную равнонапряженными нитями, уложенными вдоль геодезических линий на поверхности оправки.
Ключевые слова: композитный баллон давления, жгутовая намотка, геодезическая траектория, оптимальное армирование.
Рассмотрим композитный баллон давления в виде цилиндрической оболочки с днищами, выполненный методом намотки. Примем, что нить на днище совпадает с геодезической линией на поверхности (положение, которое нить стремится принять на гладкой поверхности при натяжении).
Под проектированием баллона давления будем понимать определение формы образующей баллона и схемы армирования баллона нитями. При этом оптимальным проектом является такой, который позволяет получить композитную конструкцию, образованную равнонапряженными нитями.
Как правило, при проектировании баллона давления в качестве исходных используют следующие данные (рис. 1):
— радиус оболочки на экваторе (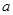 );
);
— радиус полюсного отверстия (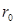 ).
).
Для геодезической намотки угол намотки на экваторе определяется по формуле:
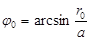 (1)
(1)
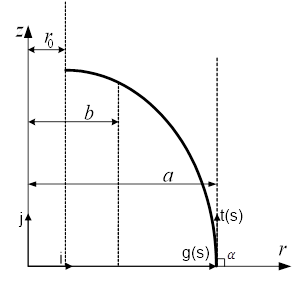
Рис. 1. — Профиль образующей днища: 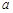 — радиус оболочки на экваторе;
— радиус оболочки на экваторе; 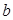 — максимальный радиус фланца;
— максимальный радиус фланца; 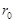 — радиус полюсного отверстия
— радиус полюсного отверстия
Принято [1, с.356; 2, с.54] искомую оптимальную форму образующей днища составлять из двух участков: участка от a до 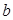 и участка от
и участка от 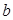 до
до 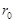 . При этом на первом участке форма днища определяется уравнением
. При этом на первом участке форма днища определяется уравнением
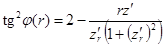 (2)
(2)
а на втором участке — уравнением
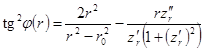 (3)
(3)
где 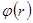 — угол намотки.
— угол намотки.
Уравнения (2) и (3) обеспечивают связь между углом намотки и формой образующей днища баллона для получения геодезической схемы армирования и равнонапряженности нитей в композитной конструкции.
Очевидным способом получения расчетной схемы на основе уравнений (2) и (3) является составление системы дифференциальных уравнений относительно 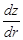 и
и 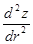 . Однако, возникает трудность с заданием начальных условий для интегрирования такой системы, поскольку в начальной точке — точке
. Однако, возникает трудность с заданием начальных условий для интегрирования такой системы, поскольку в начальной точке — точке 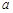 — значение производной
— значение производной 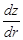 равно бесконечности (рис. 1).
равно бесконечности (рис. 1).
Получим систему дифференциальных уравнений используя натуральное уравнение плоской кривой [3, с.141]. Пусть 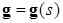 — плоская кривая, зависящая от натурального параметра
— плоская кривая, зависящая от натурального параметра 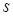 . Тогда можно записать:
. Тогда можно записать:
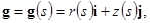
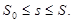
Условимся отсчитывать 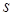 в положительном направлении, связанном с данной кривой. Произвольной остается только начальная точка отсчета.
в положительном направлении, связанном с данной кривой. Произвольной остается только начальная точка отсчета.
Обозначим через 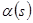 угол, образованный единичным касательным вектором [3]
угол, образованный единичным касательным вектором [3]
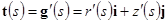
c положительным направлением оси 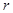 .
.
Тогда справедливы следующие равенства:
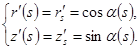 (4)
(4)
Найдем выражения для 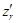 и
и 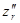 , входящих в (1) и (2), с учетом последних равенств:
, входящих в (1) и (2), с учетом последних равенств:
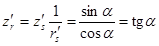
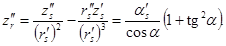
Окончательно получим:
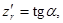 (5)
(5)
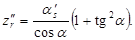 (6)
(6)
Подставляя (4) и (5) в (1) и выражая 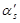 , получим:
, получим:
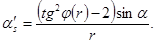 (7)
(7)
Объединяя уравнения (4) и (7), получим следующую систему дифференциальных уравнений для определения профиля днища и закона изменения угла намотки при 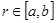 :
:
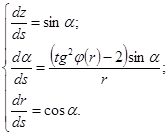 (8)
(8)
В этой системе дифференциальных уравнений начальный угол 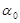 нельзя выбирать произвольно, так как
нельзя выбирать произвольно, так как 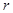 является функцией
является функцией 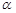 . Система (8) справедлива при
. Система (8) справедлива при 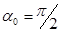 .
.
Аналогичным образом может быть получена система дифференциальных уравнений при 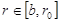 . Она имеет следующий вид:
. Она имеет следующий вид:
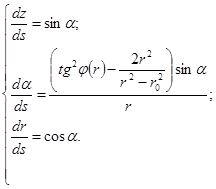 (9)
(9)
Решения систем (8) и (9) должны удовлетворять условиям сопряжения участков.
Результаты расчета профилей днищ представлены на рисунке 2, на котором профиль (1) соответствует радиусу на экваторе — 150мм, радиусу полюсного отверстия — 20мм, радиусу фланца (b1) — 24,5; профиль (2) соответствует радиусу на экваторе — 130, радиусу полюсного отверстия — 30, радиусу фланца (b2) — 36,75; профиль (3) соответствует радиусу на экваторе — 100, радиусу полюсного отверстия — 40, радиусу фланца (b3) — 49.
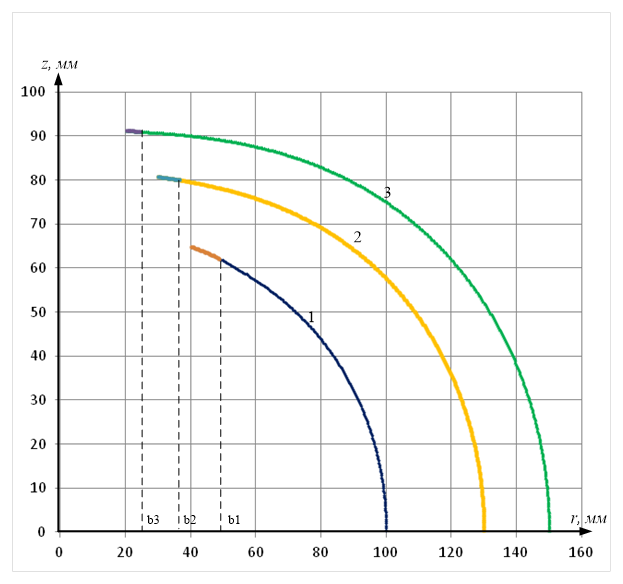
Рис. 2. Профили днищ
На рисунках 3, 4 и 5 представлены соответствующие трехмерные модели оболочек и их схемы армирования.
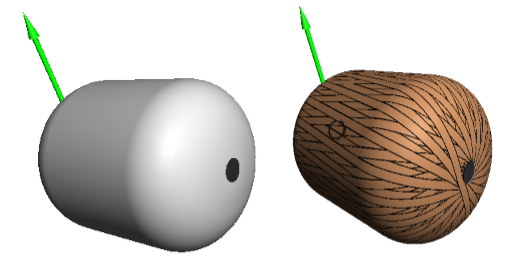
Рис. 3. Трехмерная модель оправки и схема армирования для профиля (1)
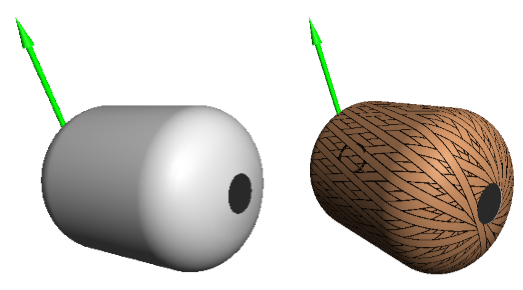
Рис. 4. Трехмерная модель оправки и схема армирования для профиля (2)
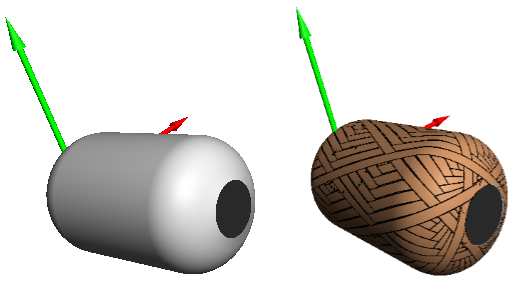
Рис. 5. Трехмерная модель оправки и схема армирования для профиля (3)
Литература:
1. Композиционные материалы: Справочник. — М.: Машиностроение, 1990.
2. В. В. Васильев, И. Ф. Образцов, В. А. Бунаков — Оптимальное армирование оболочек вращения из композиционных материалов методом намотки. — М., «Машиностроение», 1977.
3. П. К. Рашевский — Курс дифференциальной геометрии. Изд. 4-е, исправленное. — М.: Едиториал УРСС, 2003.

