Приводятся расчет объемного конечного элемента треугольной формы поперечного сечения при различных вариантах аппроксимации перемещений.
Ключевые слова: оболочка, объемный треугольный конечный элемент, несжимаемый материал, напряжения, деформации, перемещения, двумерный полином, матрица.
Если в качестве неизвестных в узле дискретного треугольного элемента принять и частные производные перемещений, то вектор узловых неизвестных конечного элемента с узлами i, j, k в глобальной системе координат будет иметь вид
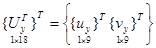 , (1)
, (1)
где
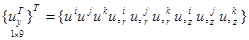 ;
;
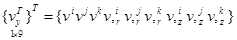 . (2)
. (2)
Для аппроксимации полей перемещений внутренних точек треугольного конечного элемента через узловые неизвестные обычно используется двумерный полином в локальной системе координат х, у. Полный двумерный полином содержит десять членов и имеет вид
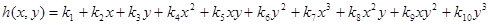 , (3)
, (3)
где коэффициенты ki являются неизвестными величинами, подлежащими определению.
Основная трудность при получении функций формы заключается в определении коэффициентов ki через компоненты вектора узловых неизвестных, так как число условий для определения коэффициентов ki всегда меньше их числа в полном двумерном полиноме(3). Поэтому приходится привлекать дополнительные условия.
Обоснованием корректности дополнительных условий являются результаты сопоставления на их основе приближенных решений с решениями других авторов или с точными решениями там, где это возможно.
В данной работе для определения коэффициентов аппроксимирующих полиномов дополнительным условием является добавление в столбец узловых неизвестных смешанной производной перемещения i-го треугольного конечного элемента 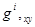 . Столбец узловых неизвестных в локальной системе координат имеет вид
. Столбец узловых неизвестных в локальной системе координат имеет вид
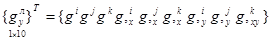 . (4)
. (4)
Перемещение внутренней точки конечного элемента выражается через узловые неизвестные величины соотношением
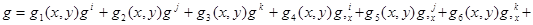
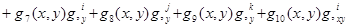 , (5)
, (5)
где под символом q понимается перемещение u или ν, а под символом qi(х, у)(i = 1…10) — аппроксимирующие функции формы.
Частные производные полного двумерного полинома (3) определяются выражениями
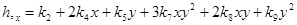 ;
;
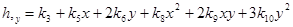 ;
;
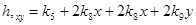 . (6)
. (6)
Для получения интерполяционных полиномов qn(х, у)(n = 1…10), составляется матричная зависимость вида
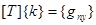 , (7)
, (7)
где
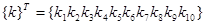 — столбец искомых коэффициентов, подлежащих определению для какой-либо одной функции qn(х, у);
— столбец искомых коэффициентов, подлежащих определению для какой-либо одной функции qn(х, у);
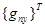 — матрица-строка узловых значений функции qn(х, у) или ее производных (элемент этой матрицы с номером n равен 1, остальные равны нулю). Например для функции q1(х, у) матрица-строка узловых значений имеет вид
— матрица-строка узловых значений функции qn(х, у) или ее производных (элемент этой матрицы с номером n равен 1, остальные равны нулю). Например для функции q1(х, у) матрица-строка узловых значений имеет вид
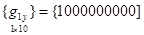 ,
,
для функции q4(х, у)
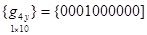 ,
,
а для функции q10(х, у)
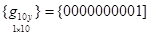 .
.
Элементы матрицы [T] представляют собой численные значения множителей при неизвестных коэффициентах ki полинома (1.3) и его производных (1.6) в узлах i, j, k конечного прямоугольного треугольника.
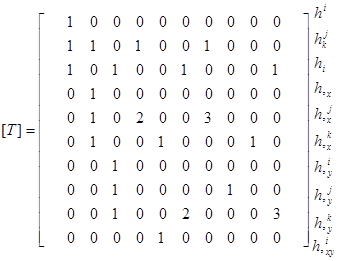 .
.
Решением системы уравнений для десяти столбцов 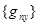 определяются коэффициенты km(m = 1…10) десяти аппроксимирующих функций q1(х, у), q2(х, у) … q10(х, у), входящих в (5).
определяются коэффициенты km(m = 1…10) десяти аппроксимирующих функций q1(х, у), q2(х, у) … q10(х, у), входящих в (5).
Смешанную производную перемещения узла i локального треугольника с использованием способа конечных разностей можно выразить через первые производные узловых перемещений по формуле
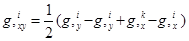 . (8)
. (8)
Если в локальной системе координат ввести вектор узловых неизвестных в виде
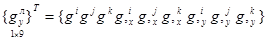 , (9)
, (9)
то на основании (8) между векторами 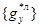 и
и 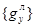 можно сформировать матричную зависимость
можно сформировать матричную зависимость
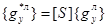 , (10)
, (10)
где матрица преобразования имеет вид
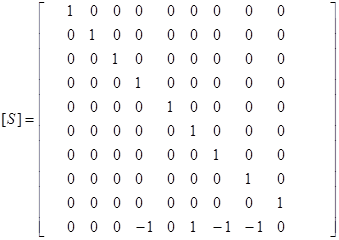 .
.
Перемещение внутренней точки конечного элемента с использованием узлового вектора (1.9) теперь можно аппроксимировать выражением
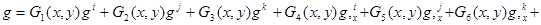
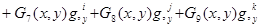 , (11)
, (11)
где под символом q по прежнему понимается перемещение u или осевое смещение ν, которые можно записать в матричном виде
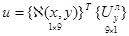 ;
;
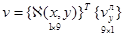 , (12)
, (12)
где строка 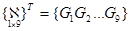 — матрица-строка аппроксимирующих функций.
— матрица-строка аппроксимирующих функций.
Аппроксимирующие полиномы Gi(x, y) (i = 1…9) определяются через полиномы qm(x, y) (m = 1…10) следующими выражениями [1]
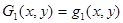 ;
; 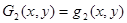 ;
;
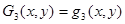 ;
; 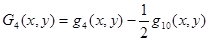 ;
;
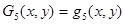 ;
; 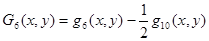 ;
;
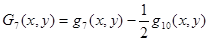 ;
;
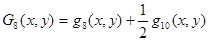 ;
;
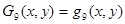 . (13)
. (13)
Окончательные выражения аппроксимирующих функций имеют следующий вид
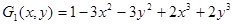 ;
;
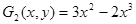 ;
;
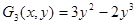 ;
;
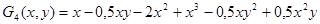 ;
;
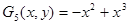 ;
;
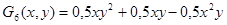 ;
;
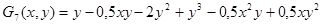 ;
;
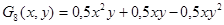 ;
;
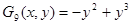 . (14)
. (14)
Частные производные перемещений внутренней точки конечного элемента определяются выражениями
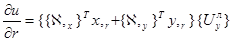 ;
;
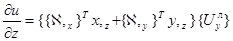 ;
;
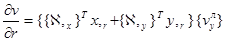 ;
;
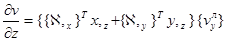 . (15)
. (15)
Литература:
1. Киселев, В. А. Строительная механика. Общий курс / В. А. Киселев. — М.: Стройиздат, 1986. — 520 с.

