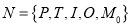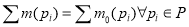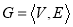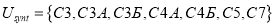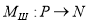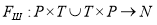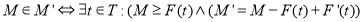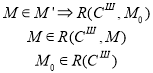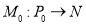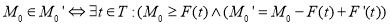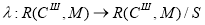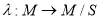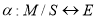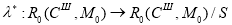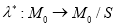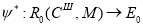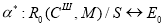В статье определены теоретические аспекты применения сетей Петри к задаче анализа технического состояния программируемых логических интегральных схем автономных технических средств. Практическое применение сетей Петри позволяет определить наиболее уязвимые места в системе технического диагностирования рассматриваемых автономных технических средств, а также решает вопрос устранения найденных уязвимостей.
Ключевые слова: телеметрическая информация, сети Петри, техническая диагностика, параллельная граф-схема алгоритма.
В рамках определения оптимальных параметров при построении модели функционирования и технического диагностирования программируемых логических интегральных схем автономных технических средств (далее — ПЛИС АТС) рассмотрим классификацию моделей для решения задачи технического диагностирования ПЛИС АТС. Анализ моделей для описания процессов функционирования и контроля систем представлен в табл. 1.
Таблица 1
|
№ п/п |
Вид моделирования |
Достоинства |
Недостатки |
|
1. |
Автоматная модель |
Моделирование любого вычислительного процесса, включая циклические |
Отсутствует возможность моделирования параллельных процессов |
|
2. |
Графическая модель |
Графическое представление автоматной модели |
Отсутствует возможность моделирования параллельных процессов |
|
3. |
Диаграмма Ганта |
Моделирование временной работы графа |
Отсутствует возможность моделирования параллельных процессов. |
|
4. |
Процессорная сеть Кана |
Моделирование распределенных вычислительных средств с управлением данными |
Отсутствует возможность моделирования систем с централизованной памятью |
|
5. |
Сеть Петри |
Моделирование систем с взаимно параллельными функционирующими компонентами |
Сложность описания простейших логических действий |
Анализ показывает, что при выполнении алгоритма криптографического преобразования процесс технического диагностирования должен осуществляться (реализовываться) параллельно с выполнением основных операций преобразования. С этой точки зрения Модель в виде сети Петри является наиболее адекватным математическим инструментом для моделирования указанного процесса [1, 2].
Данный аппарат предназначен для формализации стационарных дискретных динамических систем, обладает высокой моделируемой мощностью и необходимым уровнем абстракции. Также данный математический аппарат является универсальным, на его основе могут быть построены модельные конструкции, превосходящие по своим моделирующим возможностям различные дискретные модели с конечным или счетным множеством состояний [3]. Известно, сети Петри используются для моделирования асинхронных систем, функционирующих как совокупность параллельных взаимодействующих процессов. Анализ сетей Петри позволяет получить информацию о структуре и динамическом поведении моделируемой системы [4, 5].
Причинно-следственная связь событий в асинхронных системах задается множеством отношений вида «условия-события».
Построение моделей систем в виде сетей Петри заключается в следующем:
- Моделируемые процессы описываются множеством событий (действий) и условий, определяющих возможность наступления этих событий, а также причинно-следственными отношениями, устанавливаемыми на множестве пар «события-условия».
- Определяются события-действия, последовательность выполнения которых управляется состояниями системы. Состояния системы задаются множеством условий, формируемых в виде предикатов. Количественно условия характеризуются величиной, которая выражается числами натурального ряда.
- Условия, в зависимости от значений их количественных характеристик, могут выполняться или нет. Выполнение условий обеспечивает возможность реализации событий. Условия, с фактом выполнения которых связывается возможность реализации событий, называются предусловиями. Реализация события обеспечивает возможность выполнения других условий, находящихся с предусловиями в причинно-следственной связи. Эти условия называются постусловиями.
В сетях Петри условия − это позиции, а события − переходы.
В соответствии с этим граф сети Петри является двудольным ориентированным мультиграфом. Изображение позиции и перехода на графе показано на рис. 1 [2].
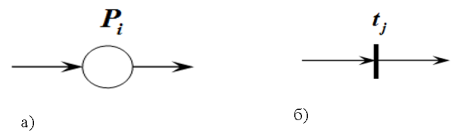
Рис. 1. Составляющие сети Петри: а) позиции, б) переходы
Ориентированные дуги могут соединять только позиции и переходы в прямом и обратном направлении (свойство двудольности). Сеть Петри является мультиграфом, так как допускается кратность дуг между позициями и переходами (вершинами графа).
Для описания и математического анализа процессов с точками ветвления и синхронизации взаимодействия аппарат сетей Петри имеет предпочтение. Структура сети представляется ориентированным двудольным графом. Множество
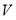
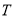
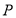
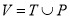
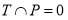
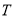
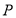
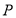
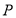
Сеть Петри определяется пятеркой
|
|
(1) |
где
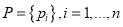
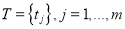
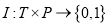
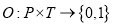
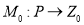
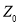
Функции
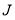
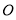
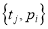
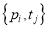
Дуги, предшествующие позиции
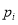
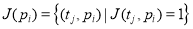
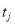
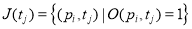
Здесь запись
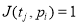
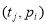
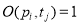
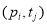
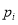
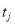
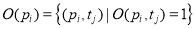
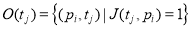
Входные позиции перехода
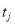
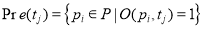
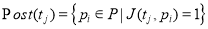
Маркирование сети представляется вектором
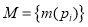
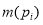
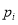
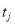
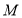
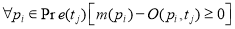
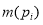
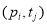
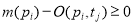
Срабатывание перехода
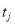
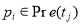
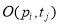
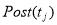
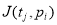
Если при маркировании
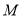
Анализ сетей Петри заключается в изучении основных свойств: безопасности, ограниченности, сохранении, активности, достижимости и покрываемости. Напомним определение каждого из этих свойств.
Безопасность. Позиция
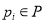
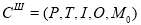
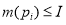
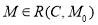
Безопасность — важное свойство для аппаратной реализации. Безопасная позиция имеет число меток 0 или 1 и может быть реализована одним триггером. Сети, в которых позиции рассматриваются (интерпретируются) как предусловия событий, маркировка каждой позиции должна быть безопасной.
Ограниченность. Безопасность — это частный случай более общего свойства ограниченности. Безопасность позволяет реализовать позицию триггером, а в более общем случае можно использовать счетчик. Любой счетчик ограничен по максимальному числу
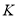
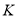
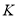
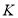
Позиция
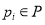
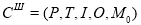
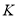
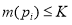
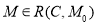
Позиция называется ограниченной, если она
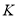
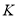
Сохранение. В сетях Петри, моделирующих запросы, распределения и освобождения ресурсов, некоторые позиции могут представлять состояние ресурсов. Например, если три метки в позиции представляют три устройства (однотипных) в вычислительной системе, то интерес представляет свойство сохранения меток. То есть метки, представляющие ресурсы, никогда не создаются и не уничтожаются. Сеть Петри называется строго сохраняющей, если для всех
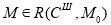
|
|
(2) |
Сеть Петри должна сохранять ресурсы, которые она моделирует. Однако не всегда имеется однозначное соответствие между меткой и количеством или числом ресурсов. В этом случае метка используется для создания кратных меток (по одной на ресурс), путем запуска перехода с большим числом выходов, чем входов. Поэтому вводятся взвешенные метки, а условие сохранения определяется через взвешенную сумму меток.
Активность. Другой задачей, возникающей при распределении ресурсов, является задача выявления тупиков.
Тупик в сети Петри — это переход (или множество переходов), которые не могут быть запущены.
Достижимость и покрываемость. Задача достижимости заключается в определении для маркировки
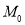
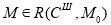
Задача покрываемости. Для сети
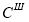
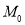
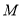
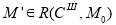
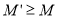
Построение модели на основе сети Петри, отвечающей требованиям по всем перечисленным свойствам, является сложной научной задачей. Рассмотрим в качестве инструмента для корректного перехода от математической модели в операторной к модели описанной на языке сети Петри синтаксически-корректно построенные параллельные граф-схемы алгоритма (далее — ПГСА).
В основе построения параллельные граф-схемы лежит способ связных декомпозиций, позволяющий определять помимо вертикальных связей по иерархии — двусторонние связи по горизонтали в пределах одного иерархического уровня.
С формальной точки зрения параллельную граф-схему можно определить, как ориентированный граф:
|
|
(3) |
где
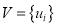
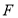
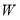
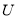
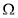

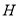
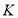
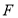
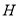
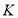
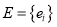
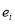
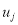
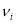
Для каждой
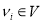
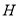
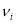
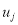
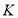
Графическое представление вершин параллельные граф-схемы различных типов представлены в литературе [5].
Управляющие вершины граф-схемы делятся на две группы: вершины «распараллеливания» (
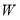
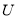
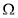

Вершины
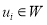
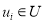
Вершины
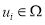
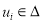
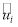
Вершины
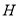
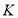
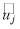
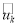
Существует четыре типа отношений между вершинами параллельной граф-схемы:
-
Отношение строго порядка:
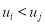
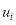
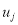
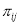
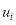
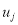
-
Отношение циклического порядка:
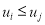
-
Отношение неопределенного порядка:
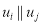
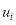
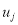
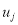
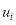
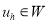
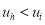
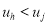
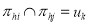
-
Отношение взаимного исключения:
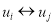
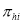
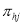
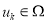
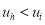
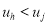
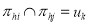
Ключевым свойством при построении параллельной граф-схемы на этапе интерпретации параметрами математической модели, построенной на основе теории сетей Петри, является ее синтаксическая корректность. Необходимо отметить, что параллельная граф-схема считается синтаксически корректной, когда обеспечивается выполнение следующих свойств [1]:
|
|
(4) |
где
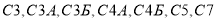
Осуществим формальный переход от модели анализа технического состояния ПЛИС АТС в операторной форме к модели, построенной на основе теории сетей Петри, изображенной на рис. 1.
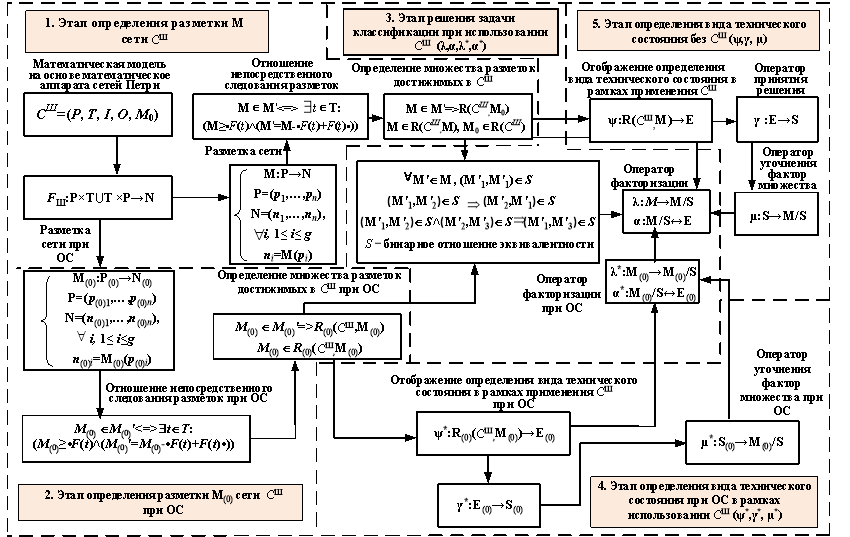
Рис. 1. Схема модели анализа технического состояния ПЛИС АТС
На первом этапе происходит определение разметки
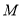
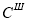
|
|
(5) |
где
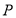
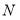
Необходимо отметить, что определение разметки
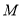
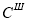
|
|
(6) |
где
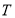
После определения разметки
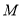
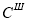
|
|
(7) |
где
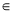
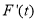
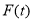
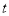
На основании отношения непосредственного следования разметок определяется отношение множества разметок, достижимых в
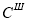
|
|
(8) |
где
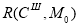
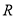
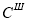
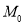
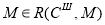
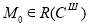
На втором этапе происходит определение разметки
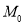
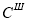
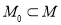
|
|
(9) |
где
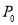
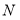
Определение разметки
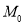
После определения разметки
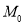
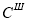
|
|
(10) |
Отношение эквивалентности задает разбиение множества
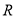
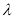
|
|
(11) |
или выражение (11) можно представить в виде:
|
|
(12) |
где
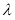
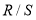
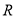
Помимо
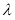
|
|
(13) |
Аналогично определим отношение эквивалентности на множестве
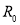
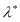
|
|
(14) |
или выражение (14) можно представить в виде:
|
|
(15) |
Принятие решения о техническом состоянии ПЛИС с математической точки зрения может быть определено через оператор
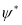
|
|
(16) |
Элемент множества
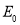
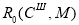
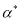
|
|
(17) |
Таким образом, построенная модель технического диагностирования в операторной форме на основе применения математического аппарата сетей Петри позволяет уточнить отношения на множествах динамической системы, в роли которой выступает ПЛИС АТС и дополнительная диагностическая информация.
Литература:
- Лоскутов А. И. Идентификация бортовой радиоэлектронной аппаратуры космических аппаратов как основа управления реконфигурацией в интересах повышения живучести — Приборы и системы. Управление, контроль, диагностика, 2018.
- Столяров А. В. Методика построения математической модели процесса функционирования беспилотного авиационного комплекса с целью решения задачи технического диагностирования. — Надежность и качество сложных систем, 2020.
- Максимов А. А. Один подход к построению конечно-автоматной управляющей сети. — Вестник Московского государственного технического университета имени Н. Э. Баумана. Серия «Приборостроение», 2012.
- Лукин М. В. Свидетельство о государственной регистрации программ для ЭВМ № 2020662638 от 16.10.2020. Российская Федерация. Программный комплекс идентификации и технического диагностирования бортовой радиоэлектронной аппаратуры космических аппаратов — РОСПАТЕНТ, 2020.
- Pelletier B. A. Petri Net Generation Tool for the Verification of Skillset-based Autonomous Systems — SkyNet, 2022.