В данной статье авторами рассмотрено воздействие внутреннего фильтра на спектральную плотность мощности и дисперсию Аллана. Проведен сравнительный анализ данных при различных порядках фильтра.
Ключевые слова: вариация Аллана, дисперсия, ИНС, шумы, спектральная плотность мощности.
Дисперсия (вариация) Аллана является общепринятым метод оценки шумов нестабильности показаний датчиков ИНС [1]. Метод заключается в непосредственном анализе временного процесса.
Временной процесс делится на временные окна с фиксированной длительностью, которая в свою очередь выбирается произвольно, но должна быть кратна периоду выборки — величине, обратной частоте выборки датчика.
Данный способ осуществляется следующим образом [2]:
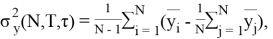
где
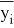
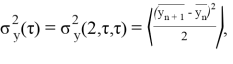
Где под {\displaystyle \langle...\rangle }<…> понимается усреднение в бесконечных пределах, {\displaystyle {\overline {y}}_{n}}
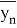
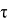
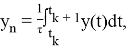
{\displaystyle \tau }где
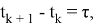
Связь между вариацией Аллана и СПМ записывается следующим образом [1]:
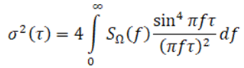
При представлении СПМ в виде дискретной последовательности:
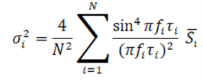
где
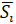
Для использования данных, полученных на выходе инерциальной навигационной системы (ИНС), необходимо произвести фильтрацию информационной составляющей от различных типов шумовых составляющих.
Одним из таких шумов является случайное блуждение нуля, другими словами аддитивный белый шум. Для гироскопов данный шум характеризует дрейф, ограниченный уровнем белого шума и измеряется в °/√ч.
В датчике ADIS16407 присутствует внутренний двухкаскадный ких-фильтр выходных данных, работающий методом окна Бартлета.
Импульсная характеристика фильтра с учетом весовых коэффициентов:
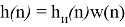
Передаточная функция фильтра:
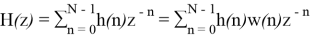
Формула треугольного окна (окна Бартлетта) имеет вид:
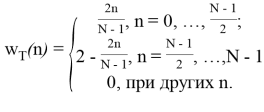
Графики вариации Аллана и СПМ для некалиброванного трёхкоординатного гироскопа датчика ADIS1607, полученные по выражениям (1)-(6) для
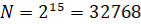
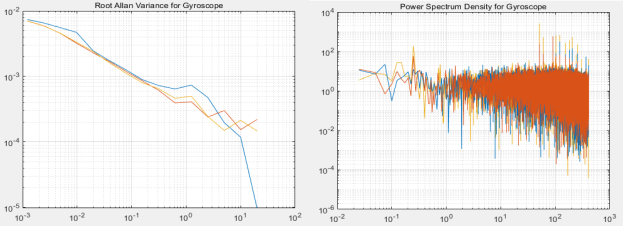
Рис. 1. Вариация Аллана и СПМ для гироскопа датчика ADIS1607 по 3 осям до корректировки
Произведем коррекцию дрейфа гироскопа, путём замера средних значений показаний по представительной выборке (
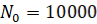
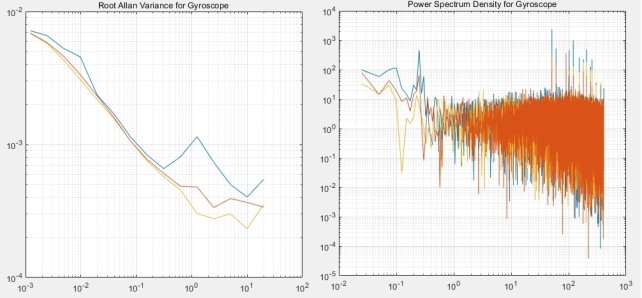
Рис. 2. Вариация Аллана и СПМ при порядке фильтра 0
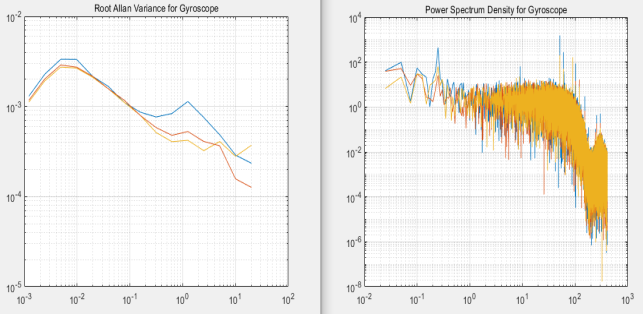
Рис. 3. Вариация Аллана и СПМ при порядке фильтра 2
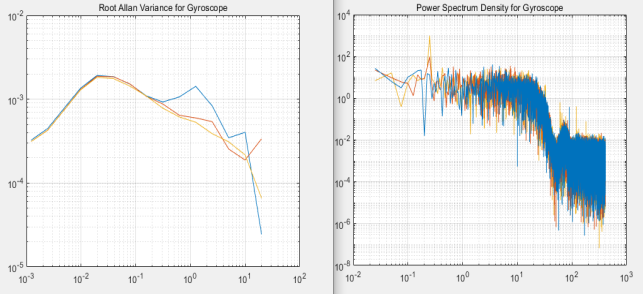
Рис. 4. Вариация Аллана и СПМ при порядке фильтра 4
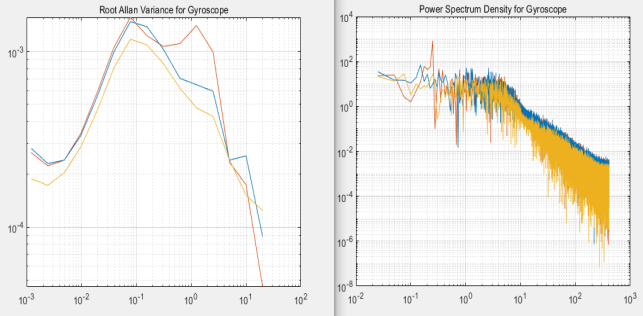
Рис. 5. Вариация Аллана и СПМ при порядке фильтра 6
Заметим, что с увеличением порядка фильтра мы замечаем более крутой срез частот в графиках СПМ, что соответствует правильной работе фильтра нижних частот. На графиках вариации Аллана появляется скат на нижних частотах, что свидетельствует о том, что вариация подвергается фильтрации.
Оценим случайное блуждение нуля по оси Z (рис.6), которое определяется на дисперсии Аллана в точке ее пересечение с интервалом времени 1 с. [3]
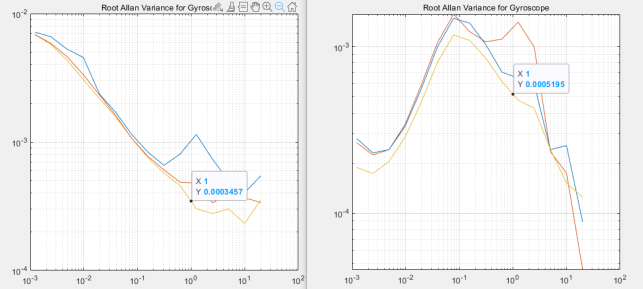
Рис. 6. Вариация Аллана для порядка фильтра 0 и 6 соответственно
Сравнив вариации подтверждается ожидаемое уменьшение марковских шумов и увеличение значений случайного блуждания нуля, также экспериментальные исследования подтвердили корректную работу фильтра выходных данных.
Литература:
- Литвин М. А., Малюгина А. А., Миллер А. Б., Чикрин Д. Е. Типы ошибок в инерциальных навигационных системах и методы их аппроксимации. М.: Информационные процессы., № Том 14, № 4., 2014. С. 326–339.
- Дисперсия Аллана [Электронный ресурс] // Википедия — свободная энциклопедия: [сайт]. [20020]. URL: https://ru.wikipedia.org/wiki/Дисперсия_Аллана#cite_note-3 (дата обращения: 27.05.2021).
- Новоселов А. С., Москалев С. А. К проблеме выбора метода оценки дрейфовых характеристик волновых твердотельных гироскопов ГЕ 006 на основе экспериментального подтверждения. М.: Надежность и качество сложных систем., № 1, 2021. С 57–65.

