A Note on the upper bound of the palette index of nearly bipartite graphs
Автор: Смбатян Хачик Смбатович
Рубрика: 1. Математика
Опубликовано в
XXI международная научная конференция «Исследования молодых ученых» (Казань, июнь 2021)
Дата публикации: 19.05.2021
Статья просмотрена: 48 раз
Библиографическое описание:
Смбатян, Х. С. A Note on the upper bound of the palette index of nearly bipartite graphs / Х. С. Смбатян. — Текст : непосредственный // Исследования молодых ученых : материалы XXI Междунар. науч. конф. (г. Казань, июнь 2021 г.). — Казань : Молодой ученый, 2021. — С. 1-4. — URL: https://moluch.ru/conf/stud/archive/396/16562/ (дата обращения: 20.04.2024).
Given a proper edge coloring α of a graph G, we define the palette S_G (v,α) of a vertex v ∈ V (G) as the set of all colors appearing on edges incident with v. The palette index s ̌(G) of G is the minimum number of distinct palettes occurring in a proper edge coloring of G. A graph G is called nearly bipartite if there exists v ∈ V (G) so that G-v is a bipartite graph. In this paper, we give an upper bound on the palette index of a nearly bipartite graph G by using the decomposition of G into cycles.
Keywords: edge coloring, proper edge coloring, palette, palette index.
Throughout this paper, a graph

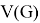
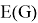

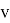

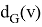

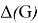
An
edge coloring
of a graph




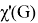

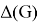
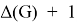
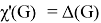
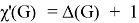
In this paper we consider a chromatic parameter called the palette index of a simple graph

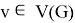
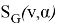

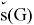
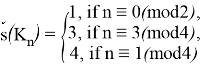
Moreover, they also showed that the palette index of a d-regular graph is



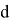

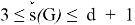
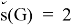


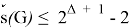
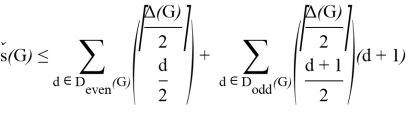
where
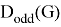

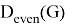

In [3], Bonvicini and Mazzuoccolo proved that if

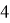

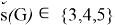
Definition 1. (Edge subdivision). Let

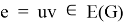
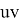

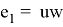
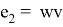
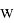
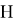
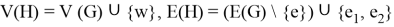
Definition 2.
(Nearly bipartite). A graph

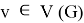
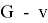
We also need a classic result from factor theory, proof of which can be found in [10].
Theorem 1.
(Petersen’s Theorem). Let

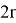

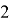
For a graph

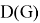

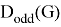

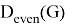

Theorem 2.
If

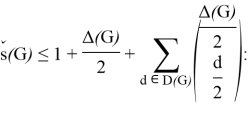
Moreover, this upper bound is sharp for any odd length cycle.
Proof. In the proof of this theorem, we follow the idea from [6] (Theorem 2.2). We first construct a new multigraph
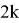
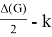
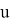
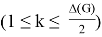
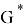
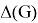
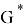
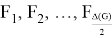
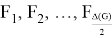
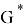
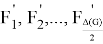
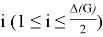
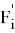

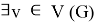
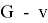
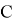
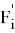
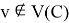
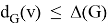
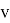
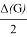
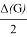
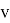
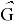
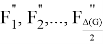
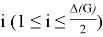
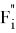
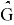
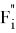
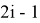
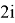
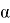
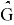
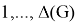
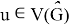
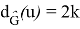
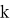
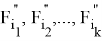
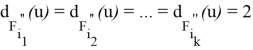
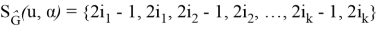
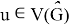
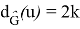
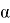
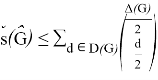
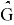
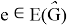
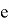
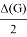
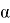
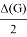
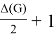

Hence,
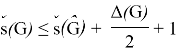
Now, if

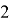
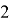
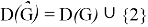
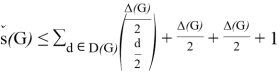


From a given nearly bipartite graph G, we can construct an even super graph G' which can be represented as a union of edge-disjoint 2-factors. Let us first construct a new graph G' as defined in [6] by taking two vertex-disjoint copies
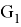
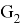

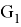
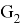
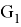
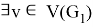
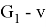
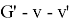
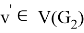
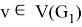
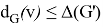
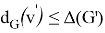
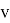
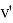
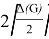
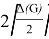
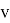
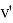
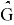
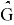
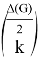
Corollary 1 . For any nearly bipartite graph G, we have
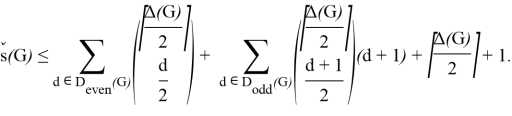
Proof.
Consider the graph
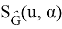
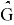
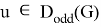
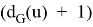
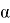

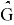
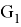

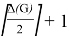
Corollary 2. For any nearly bipartite graph G, we have
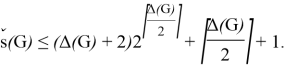
Conclusion
In the current article, we examined the palette index of nearly bipartite graphs. We improved the upper bound of the palette index of an even nearly bipartite graph. Moreover, we showed that the upper bound is sharp for any odd length cycle. Also, we obtained the upper bound for any nearly bipartite graph as a corollary from this result.
References:
- West D. B. / Introduction to Graph Theory / D. B. West. —: N.J.: Prentice-Hall, 2001.
- M. Hornak, R. Kalinowski, M. Meszka, M. Wozniak. / Minimum Number of Palettes in Edge Colorings // Graphs and Combinatorics. — 2014. — № 30. — С. 619–626.
- S. Bonvicini, G. Mazzuoccolo / Edge-Colorings of 4-Regular Graphs with the Minimum Number of Palettes // Graphs and Combinatorics. — 2016. — № 32. — С. 1293–1311.
- I. Holyer / The NP-Completeness of Edge-Coloring / SIAM Journal on Computing. — 1981. — С. 718–720.
- M. Avesani, A. Bonisoli, G. Mazzuoccolo. / A Family of Multigraphs with Large Palette Index // Ars Mathematica Contemporanea. — 2019. — № 17. — С. 115–124.
- C. J. Casselgren, P. A. Petrosyan. / Some results on the palette index of graphs // Discrete Mathematics and Theoretical Computer Science.
- S. Fiorini, R. J. Wilson / Edge-Colorings of Graphs // Research Notes in Mathematics.
- R. Hammack, W. Imrich, S. Klavzar / Handbook of Product Graphs Second Edition // CRC Press. — 2011.
- Vizing, V. G. / On an estimate of the chromatic class of a p-graph // Diskret. Analiz 3. — 1964. С. 25–30.











