Колебания механизмов
Авторы: Горшков Александр Деомидович, Сиваконьев Андрей Вячеславович, Некрасов Михаил Дмитриевич
Рубрика: 7. Технические науки
Опубликовано в
XXI международная научная конференция «Исследования молодых ученых» (Казань, июнь 2021)
Дата публикации: 15.05.2021
Статья просмотрена: 13 раз
Библиографическое описание:
Горшков, А. Д. Колебания механизмов / А. Д. Горшков, А. В. Сиваконьев, М. Д. Некрасов. — Текст : непосредственный // Исследования молодых ученых : материалы XXI Междунар. науч. конф. (г. Казань, июнь 2021 г.). — Казань : Молодой ученый, 2021. — С. 14-16. — URL: https://moluch.ru/conf/stud/archive/396/16549/ (дата обращения: 18.04.2024).
В статье были рассмотрены вопросы воздействия редко в своем роде изменяющихся сил и моментов детали, а также наиболее популярные в своем роде механизмы совершающие вынужденные упругие колебания, которые в дальнейшем использовании становятся особенно сильными при появлении каких — либо резонансов, когда частоты возмущающих сил или моментов частично или полностью совпадают с частотами собственных колебаний системы. А также вопрос вероятности возникновения резонансных режимов, которые в дальнейшем приобретают весомую роль с увеличением повышения скорости машины. Анализ наиболее используемого, а также вполне знакопеременного движения динамических систем и сил, связанных с этим движением, очень актуален и важен для определения их влияния на характеристики и надежность рассматриваемых систем. Описанными в данной работе методами расчета мы сможем прийти к общему выводы, а в дальнейшем и решить, связанные с колебаниями основных деталей механизмов и машин.
Ключевые слова: уравновешивание, кинематические колебания, движение, динамическое проектирование механизма машины.
The article deals with the impact of periodically changing forces and moments of the part, as well as the mechanisms that perform forced elastic vibrations, which become especially strong when resonances occur, when the frequencies of the disturbing forces or moments coincide with the frequencies of the natural vibrations of the system. And also the question of the probability of collision of resonant modes that occur with an increase in the increase in the speed of the machine. The analysis of the alternating motion of dynamical systems and the forces associated with this motion is important for determining their influence on the characteristics and reliability of the systems under consideration. The described calculation methods can be used to solve many problems related to the fluctuations of the main parts of mechanisms and machines.
Keywords: balancing, kinematic vibrations, motion, dynamic design of the machine mechanism.
Колебания упругой системы скорее всего востребованы мгновенным импульсом или внезапным воздействием и в дальнейшем устранением внешних силы или момента.
Колебания, которые остаются непоколебимы только силой упругости детали (или машины на подвеске), к которой мы можем применить понятие внешний импульс (сила или момент), получили название свободными или собственными . Эти колебания очень подробно растолковываются и описываются однородными дифференциальными уравнениями. Если колебания системы будут неисправимы или незаменимы, то наша система называется консервативной . При демпфировании система называется неконсервативной . [1, c. 123–145]
Вынужденными колебаниями называются такие, когда расхождения или неиспользование упругой системы полностью находятся под действием переменных во времени внешних сил или моментов. Дифференциальные уравнения вынужденных колебаний исходя из данного контекста являются неоднородными, причем член в правой части является функцией времени.
Простейшей формой данного движения является гармоническое колебание, изменяющее свои нормы и правила по закону синуса или косинуса. Всякое гармоническое движение есть движение хаотичное или непостоянное, но не всякое периодическое движение является движением гармоническим. Если изменяющаяся деталь полностью подвластна воздействию двух гармонических движений, частоты которых (
ω
1
и
ω
2
) близки между собой (различие частот на 1–2 %), то может возникнуть
биение
с частотой
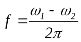
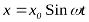
Полный цикл колебаний закончит свое существование при изменении ωt за 2 π . В этом случае промежуток времени t равен периоду колебаний (с)
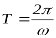
Величину
ω
с
называют круговой частотой собственных колебаний (частота собственных колебаний
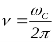
Если колебания похожей массы системы протекают с затуханием, то дифференциальное уравнение колебаний принимает вид
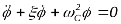
В случае возникновения вынужденных колебаний на колеблющийся диск одномассовой системы будет оказывать свое действие или какое — либо влияние возмущающий момент М 0 Sin ωt и дифференциальное уравнение движения принимает вид:
без затухания
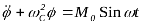
с затуханием
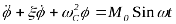
При дальнейшем изучении и доработке вынужденных колебаний учет собственных колебаний наиболее актуален в том случае, когда числовые значения ω и ω С близки друг к другу, т. е. когда могут возникать биения . При затухании колебаний биения со временем исчезают, и в системе остаются постепенно заданные вынужденные колебания. [2, c. 90–98]
Из общего числа форм собственных колебаний наиболее практику представляют только те, которые находят применение с частотами возмущающих моментов и в дальнейшем происходит резонанс в рабочем диапазоне оборотов системы. При возникновении резонанса возникает форма вынужденных колебаний, которая в свою очередь практически совпадает с формой собственных колебаний. При этом в валах привода возникают наиболее активные напряжения, опасные для его прочности.
Все перечисленное выше, а отходя от контекста и другие факторы способствуют возникновению периодических сил механического, электромагнитного, аэродинамического и гидравлического происхождения с широким диапазоном частот возбуждения. При нахождении частоты собственных изгибных колебаний вал могут разбирать как балку, нагруженную по той схеме, которая ближе всего к реальному нагружению.
На основании данного материала мы можем прийти к выводу, что при больших нагрузках на виброизолятор нелинейной становится и характеристика демпфера, выражающая зависимость силы сопротивления от скорости перемещения виброизолятора. Мы смогли решить задачу нелинейности, которая проявляется особенно ярко при увеличении демпфирования, которое становится необходимым в тех случаях, когда не удается избежать резонанса.
Литература:
- Гололобов Г. И. Федоров Н. Н. Моделирование кинематики плоских рычажных механизмов на ПЭВМ: Спр. пособие. Омск, 2003.
- Гриб В. В., Самылин Е. А., Костюк И. В. Кинематический анализ методом планов. Методическое пособие для самостоятельной работы студентов. 2002.
- Гришин В. А. Параметрический синтез кулачковых механизмов: Технические задания и методическое руководство к выполнению курсовой работы по дисциплине «Основы проектирования и конструирования» для подготовки студентов по направлению «Экономика и управление на предприятии (в машиностроении)» / В. А. Гришин, А. Г. Вискарева. — Н. Новгород: ННГУ, 2010. — 56 с.: ил.
- Грудинин Г. В. Динамический расчет приводов. Учебное пособие. / ИрГТУ.- Иркутск: изд-во ИрГТУ, 1996.- 67 с.
- Диментберг Ф. М. Теория пространственных шарнирных механизмов. — М.: Наука, 1982.- 336 с.
- Динамический синтез плоских рычажных механизмов: Методические рекомендации к курсовому проектированию по теории механизмов и машин/Курск. гос. техн. ун-т; Сост. В. Я. Мищенко, С. А. Зайцев. Курск, 2003, 18 с.











