Гибридизация несмещённого фильтра с конечной импульсной характеристикой и фильтра Кальмана



В задачах радиолокационной оптимизации часто возникает вопрос о выборе между фильтром с конечной импульсной характеристикой и фильтром Кальмана. Оба этих фильтра имеют свои сильные и слабые стороны. В этой работе рассматривается попытка создание их гибридного фильтра, способного автоматически дать оптимальную оценку позиции объекта, основываясь на двух вышеуказанных.

Ключевые слова: фильтр, Кальман, импульс, гибрид.

1. Введение и Обозначения

— n-мерное вещественное векторное пространство

— Множество всех непрерывных функций на множестве [5]

и — Мат. Ожидание и дисперсия случайной величины

[8]

— Ковариационна матрица случайного вектора [7]

— След квадратной матрицы [6]

— транспонированная матрицы [6]

— Единичная матрица [6]

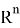
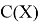
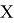
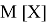
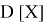
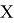
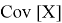
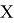
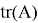
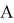
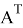
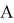
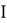
Допустим имеем некоторый движущийся объект в с заданной моделью:

,(1)

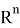
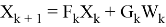
где k-я позиция вектора состояния, - вещественная матрица называемая матрицей перехода, вещественная матрица и есть

— мерный случайный вектор т. ч. и .

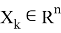
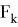
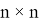
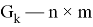
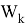
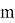
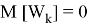
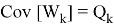
Допустим что некоторое устройство измеряет данный объект с заданной моделью:

,(2)

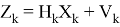
где измерение k-той позиции, есть матрица и есть

-мерный случайный вектор т. ч. . и .

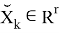
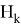
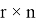
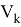
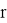
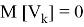
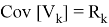
2. Фильтр Кальмана

Рассмотрим оценку вектора состояния на основе измерений

,(3)

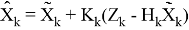
где и вещественная матрица.

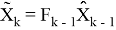
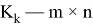
Теорема 1 (см [1] или [2]) Если взять матрицу равной

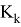
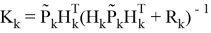
Где определяется рекурсивно

, ,

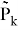
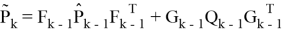
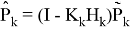
тогда о есть оценка (3) будет оптимальной. Данный способ оценки вектора состояния называется фильтром Кальмана. Заметим, что для работы фильтра Кальмана необходимы матрицы и , но вопрос об их оценке рассматривается отдельно.

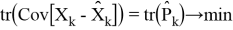
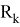
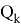
Хоть фильтр Кальмана и является оптимальной оценкой для этой модели, но общая модель движения объекта задается в виде

,(4)

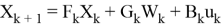
где вектор — вектор управления, отвечающий за маневрируемость объекта, а -корректирующая матрица. Таким образом фильтр Кальмана даeт оптимальную оценку в том случае, когда , в ином же случае он может предложить смещёную оценку. Вопрос об оптимальности этой оценки также рассматривается отдельно, в частности в направлении машинного обучения.

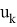
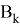
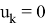
3. Несмещеный фильтр с конечной импульсной характеристикой

Рассмотрим несмещеный фильтр с конечной импульсной характеристикой определенный в работе [6]

(5)

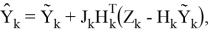
где

и определяется по формуле

(6)

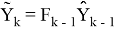
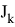
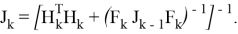
Матрица не обновляется после итераций. Как было показано в работе [6], оценка (5) является несмещеной, но она не обладает свойством оптимальности, которой обладает оценка (3), хотя для его вычисления не требуются матрицы и Кроме того, при рассмотрении модели (4) данная оценка обладает меньшей ошибкой чем у оценки (3) при .

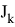
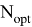
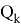
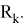
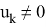
Таким образом заключение следующее — при

стоит выбрать фильтр Кальмана как основную оценку, если же , то фильтр с конечной импульсной характеристикой будет более правильным выбором. Если был бы известен, то данный вопрос решился бы непосредственно, в этой работе рассматривается случай, когда неизвестно, а оценки матриц и неточны (как это обычно бывает в практике).

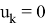
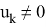
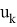
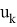
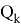
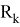
4. Гибридизация фильтра Кальмана и несмещеного фильтра с конечной импульсной характеристикой

Данный вопрос о выборе между оценками (3) и (5) приводит нас к созданию их гибрида, который будем искать в виде

(7)

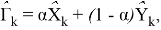
где . О том как определить

далее пойдет и речь.

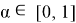
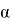
Обозначим вероятность P( Если было бы более эффективной оценкой, то выбрав как основную оценку мы бы ошиблись на , в ином же случае ошибка представлялась бы в виде . Будем рассматривать данную задачу с точки зрения минимизации максимальной вероятностной ошибки, то есть:

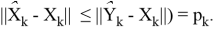
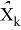
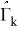
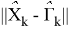
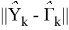
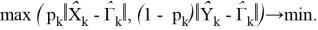
Подставив (4.1) в полученное выражение имеем

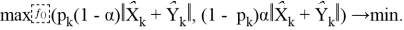
Данная задача минимизации эквивалентна задаче

.

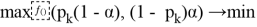
Легко заметить, что при вышеуказанное выражение будет принимать своё наименьшее значение.

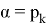
Таким образом, чтобы вычислить гибридную оценку надо сперва оценить . Так как оценки и являются несмещенными, можем предполагать что , где

и . Оценим вероятность .

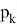
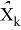
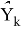
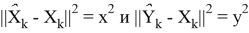
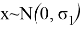
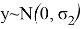
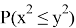
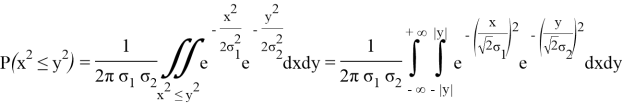
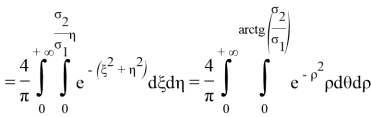
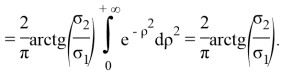
Таким образом, чтобы найти необходимо оценить

и . Это можно произвести эвристическим образом на основе последних измерений:

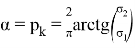
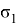
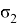
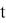
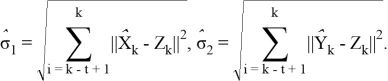
5. Анализ эффективности и заключение

Ниже приведены наблюдения ошибок , и соответственно для фильтра Кальмана, НФКИХ и гибридного фильтра для модели, рассмотренной в работе [4 стр. 48–49] с примером матриц

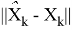
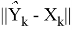
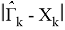
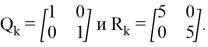
Для фильтра Кальмана оценки матриц были вычислены как

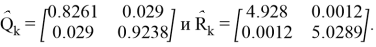
А для НФКИХ было взято равным 8.

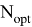
Было рассмотрено 2 возможных случая — на Рис.1. была рассмотрена модель без маневров (т. е. при любом ), а на Рис.2. было произведено 3 случайных маневра. На обеих рисунках координата — номер измерения k, а y — ошибка соответствующего фильтра.

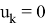
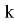
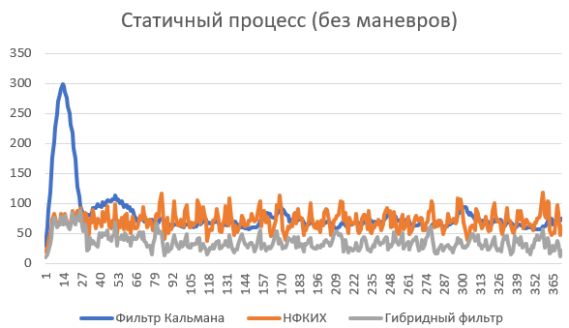
Рис. 1

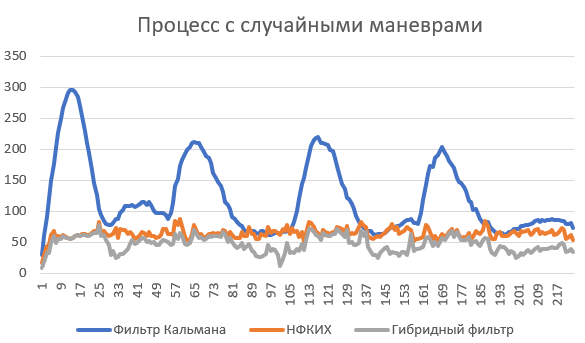
Рис. 2

Как можем видеть при практическом наблюдении гибридный фильтр проявляет себя лучше чем оба других фильтра во всех случаях. Значимость данной работы заключается в том что решаются сразу два вопроса — точность оценок и и распознование манёвров.

Литература:

1. Kalman, R.E. (1960). «A new approach to linear filtering and prediction problems». Journal of Basic Engineering. 82 (1): 35–45. doi:10.1115/1.3662552. Archived from the original (PDF) on 2008–05–29. Retrieved 2008–05–03.
2. Kalman, R.E.; Bucy, R.S. (1961). «New Results in Linear Filtering and Prediction Theory»
3. Hakobyan Y. R. Basics of Numerical Analysis (2005)
4. Ramachandra K. V. (2000) «Kalman Filtering Techniques for Radar Tracking» 1st Edition
5. Дарбинян А. А., Акопян А. Р. (2019) “Модификация фильтра Калмана для полярных и сферических систем координат” Вестник РАУ
6. Unbiased FIR Filtering: An Iterative Alternative to Kalman Filtering Ignoring Noise and Initial Conditions. October 2017IEEE Control Systems Magazine 37(5) DOI: 10.1109/MCS.2017.2718830