Разработана математическая модель метода зарядки емкостного элемента от источника ЭДС ограниченной мощности. Проведен анализ возможности практической реализации данного метода. Приводится сравнение с зарядом непосредственно от идеального источника ЭДС.
Ключевые слова: зарядка, конденсатор, автономное питание.
A mathematical model of the method of charging a capacitive element from an EMF source of limited power has been developed. The analysis of the possibility of practical implementation of the method is carried out. A comparison is made with the charge directly from an ideal EMF source.
Keywords: charging, capacitor, self-contained power supply.
Введение.
Затрагиваемая проблема состоит в том, что не вся энергия, имеющаяся в источнике ЭДС, является доступной вследствие ограничений скоростью заряда. Особенно актуальным этот вопрос представляется в ситуациях, когда распределение мощности по времени не является постоянной величиной и наблюдаются изменения, обусловленные случайными факторами. Примером могут служить такие возобновляемые источники энергии, как солнечный свет, ветер, движение воды и т. д. В таких случаях возникает риск потери энергетических запасов по причине вероятностного характера природных процессов [1] и возможного дефицита мощности в случайные моменты времени. Если при этом необходимо обеспечить автономность и непрерывность функционирования потребляющего устройства, то важным является своевременная аккумуляция энергии с целью последующего распределения и использования.
Дополнительную сложность составляет наличие нелинейности в зависимостях между физическими параметрами генераторов электроэнергии. Например, типичная вольтамперная характеристика фотобатареи [2], изображенная на рисунке 1, показывает, что максимальная мощность, соответствующая точке N, лежащей на прямой 0A, достижима при условии соблюдения определенных значений напряжения и тока, что не позволяет подключать накопительный конденсатор непосредственно к генератору.
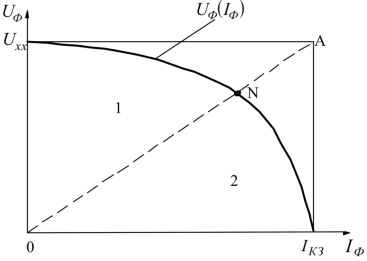
Рис. 1. Вольтамперная характеристика фотобатареи
Цель работы состоит в изучении метода ускоренного заряда емкостного элемента от источника ЭДС ограниченной мощности посредством математического моделирования энергетических процессов и оценке возможности практической реализации данного метода.
Основная часть.
Наиболее простым способом заряда конденсатора является непосредственное подключение к источнику ЭДС. В тех ситуациях, когда ограничениями мощности заряда можно пренебречь, справедлива формула [2]:
![]() (1)
(1)
где ![]() — выбранный момент времени,
— выбранный момент времени, ![]() — напряжение на выходе источника,
— напряжение на выходе источника, ![]() — напряжение на выводах конденсатора,
— напряжение на выводах конденсатора, ![]() ,
, ![]() — его внутреннее сопротивление и емкость.
— его внутреннее сопротивление и емкость.
Если падение напряжения источника ЭДС значительно вследствие ограничения его мощности:
![]() (2)
(2)
где ![]() — максимальная мощность источника,
— максимальная мощность источника, ![]() — напряжение на выходе источника ЭДС,
— напряжение на выходе источника ЭДС, ![]() — потребляемая сила тока:
— потребляемая сила тока:
![]() (3)
(3)
![]() (4)
(4)
Из 2, 3 и 4:
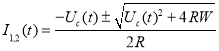 (5)
(5)
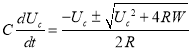 (6)
(6)
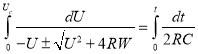 (7)
(7)
После разделения переменных и интегрирования по указанным пределам:
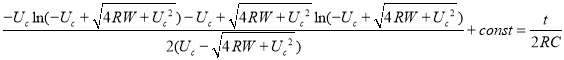 (8)
(8)
где, исходя из начальных условий ![]() :
:
![]() (9)
(9)
На рисунке 2 показано, как будет заряжаться конденсатор согласно (8), если подключен к источнику мощностью 0,01 Вт или 1 Вт при R=40 Ом, C=1 Ф. Для сравнения приведены вычисления по формуле 1 при E=const=5 вольт:
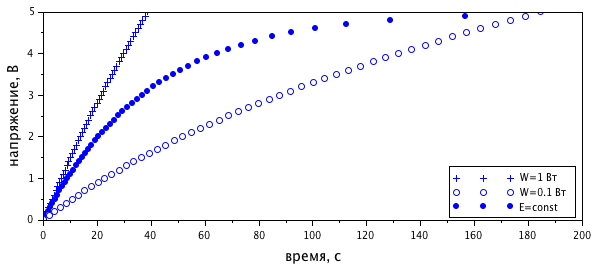
Рис. 2. Зависимость напряжения на выводах конденсатора от времени
Из этого примера видно, что возможны по меньшей мере два случая: более медленный заряд, чем при E=const, и более быстрый. Первый является очевидным, потому что при крайне низкой мощности источника потребуется повышенное количество времени на совершение работы по созданию электрического поля конденсатора. Больший интерес представляет второй случай с позиции принципиальной возможности практической реализации.
На рисунке 3 видно, что ускорение заряда происходит по причине повышенного напряжения источника ЭДС по сравнению с E=const=5 Вольт.
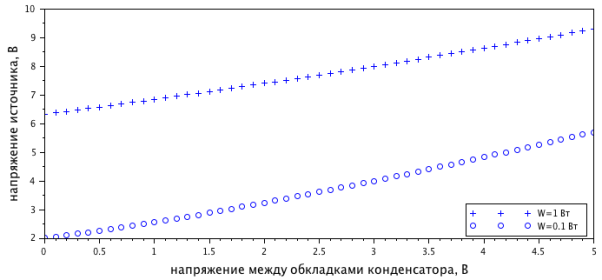
Рис. 3. Зависимость напряжения источника ЭДС от напряжения на обкладках конденсатора при фиксированной мощности
Таким образом, для указанного примера можно сделать вывод о том, что для значительного уменьшения времени заряда требуется повышение напряжения менее, чем в 2 раза. При этом максимальная сила тока согласно уравнению 5 составит менее 160 мА. Эти параметры являются допустимыми и реализуемым на практике.
Из закона сохранения энергии:
![]() (10)
(10)
![]() (11)
(11)
где ![]() — мощность, рассеиваемая на активном сопротивлении конденсатора,
— мощность, рассеиваемая на активном сопротивлении конденсатора, ![]() — напряжение, падающее на этом сопротивлении,
— напряжение, падающее на этом сопротивлении, ![]() — мощность, затрачиваемая на создание электрического поля конденсатора, которая из определения мощности составляет, с учетом (6):
— мощность, затрачиваемая на создание электрического поля конденсатора, которая из определения мощности составляет, с учетом (6):
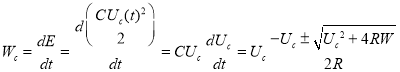 (12)
(12)
С учетом (11), уравнение электрического состояния согласно второму правилу Кирхгофа имеет вид:
![]() (13)
(13)
Из рисунка 4 видно, что эффективность процесса заряда увеличивается с ростом напряжения на выводах конденсатора, потому что большая часть мощности уходит на внутреннее активное сопротивление. Следовательно, для предотвращения перегрева и оптимизации энергетических процессов в устройстве, работающем от восполняемых источников, необходимо не допускать глубокого разряда.
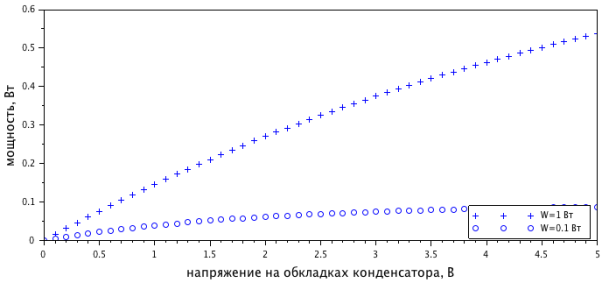
Рис. 4. Мощность, потребляемая конденсатором
Заключение.
Описанные меры по ускорению и оптимизации процесса заряда конденсатора от источников ЭДС, имеющих ограниченную мощность, сводятся к увеличению напряжения на выводах конденсатора и контролю глубины разряда. Дальнейшие исследования предполагается вести в области схемотехнических решений. При этом произведенная оценка выходных параметров необходимого преобразователя, включающих максимальный ток и напряжение, показывает принципиальную возможность практической реализации указанных мер, и, учитывая нелинейный характер полученных зависимостей тока от напряжения и диаграммы на рисунке 1, можно предположить, что зарядное устройство оптимальнее разрабатывать на основе микро ЭВМ и цифровых методов обработки.
Литература:
- Справочник по ресурсам возобновляемых источников энергии России и местным видам топлива. Показатели по территориям. — М.: ИАЦ Энергия, 2007. — 272 с.
- Дзензерский В. А., Плаксин С. В., Житник Н. Е., Погорелая Л. М. Метод зарядки химических источников тока в составе фотоэлектрической установки // Электроэнергетика. — 2009. — № 2. — С. 73–77.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи: учебник для бакалавров. — 12-е изд. — М.: Издательство Юрайт, 2016. — 701 с.

