1. Введение
На сегодняшний день проблема сбоев в поставках актуальна как никогда раньше, поскольку сбои могут возникнуть абсолютно в любой цепочке поставок. Причины возникновения сбоев совершенно различны: действия рабочих, поломка машины, природные или техногенные катастрофы и др. Сбои могут приводить к последствиям разного масштаба и необходимо их все учитывать. Модель, исследуемая в данной работе, применима как к большим, так и к малым нарушениям.
Для того чтобы фирмам наилучшим образом справляться со сбоями, необходимо усовершенствовать методы управления цепочками поставок.
2. Обзор литературы
Парлар и Беркин [2] представляют первую из серии моделей, которые добавляют нарушения поставок в классические модели управления запасами. Их модель получила название EOQD, она подобна модели EOQ, в которой поставщик испытывает периодические сбои. Спрос теряется, если у ритейлера не хватает запасов для того, чтобы его удовлетворить во время сбоев поставщика. Берк и Арриола-Риза [1] показали, что стоимостная функция [2] имеет ошибки в двух предположениях, и предложили новую исправленную функцию ожидаемых затрат. Но решение для модели [1] нельзя представить в аналитической виде, поэтому Снайдер [5] вводит аппроксимацию, исследует новую полученную модель и находит решение в аналитической форме.
Парлар и Перри [3] расширяют модель EOQD, ослабляя предположение ZIO и принимая время между попытками заказа за переменную решения. Уже в следующей работе [4] они рассматривают EOQD с одним, двумя или несколькими поставщиками и ненулевыми точками повторного заказа. Томлин [6] в своем исследовании рассматривает стратегии для преодоления сбоев в поставках.
3. Описание модели
3.1. Модель EOQD
Рассмотрим исправленную модель Берка и Арриола-Ризы [1].
Даны фиксированная стоимость заказа ![]() , стоимость хранения
, стоимость хранения ![]() за единицу в год и постоянная детерминированная скорость спроса
за единицу в год и постоянная детерминированная скорость спроса ![]() единиц в год. Без потери общности предполагается, что единица времени — один год.
единиц в год. Без потери общности предполагается, что единица времени — один год.
Предполагается, что у поставщика происходит сбой на определенный период времени, после того как он нормально работал в течение длительного периода времени. Принято обозначать периоды сбоя как сухие, а периоды обычного функционирования как влажные. Во время сухого периода получить от поставщика товары невозможно, а ритейлеры несут издержки дефицита ![]() за спрос, возникающий в этот период. Продолжительности периодов поставщика экспоненциально распределены с параметрами
за спрос, возникающий в этот период. Продолжительности периодов поставщика экспоненциально распределены с параметрами ![]() для влажного и
для влажного и ![]() для сухого. Каждый заказ предназначен для одного и того же объема
для сухого. Каждый заказ предназначен для одного и того же объема ![]() , заказы размещаются тогда, когда уровень запасов у ритейлера достигает 0, при этом заказы, размещенные во влажные периоды, восполняются немедленно. Целью модели является выбор
, заказы размещаются тогда, когда уровень запасов у ритейлера достигает 0, при этом заказы, размещенные во влажные периоды, восполняются немедленно. Целью модели является выбор ![]() для минимизации ожидаемых годовых затрат.
для минимизации ожидаемых годовых затрат.
Функция ожидаемой годовой стоимости такой модели:
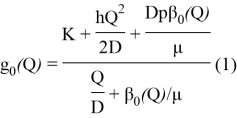
где
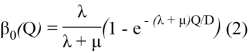
вероятность того, что когда уровень запасов ритейлера достигнет 0 поставщик будет находится в сухом периоде. Часто аргумент ![]() в
в ![]() подавляется, когда это ясно из контекста.
подавляется, когда это ясно из контекста.
Представленную модель можно оптимизировать численно с помощью методов линейного поиска, но она не может быть решена в аналитическом виде, поэтому необходимо рассматреть ее аппроксимацию.
3.2. Аппроксимационная модель EOQD
Снайдер предлагает аппроксимировать стоимостную функцию, заменив ![]() на
на
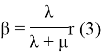
где r — константа, подчиняющаяся условию 0 < r < 1. Тогда приближенная функция стоимости будет
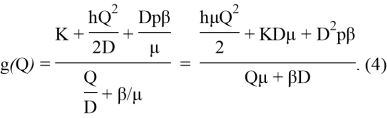
Снайдер доказал, что полученная функция стоимости выпуклая, и предоставил решение в аналитической форме для оптимального значения ![]() , которая минимизирует (4):
, которая минимизирует (4):
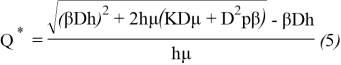
4. Исследование на численных данных
4.1. Генерирование данных.
Исследуем модель Снайдера, используя 1000 случайно сгенерированных наборов данных. Наборы были созданы путем случайного выбора параметров ![]() из выборок, с объемом равным 10 для каждой, полученных из следующих распределений:
из выборок, с объемом равным 10 для каждой, полученных из следующих распределений:
− ![]()
− ![]()
− ![]()
− ![]()
− ![]()
− ![]()
Границы были выбраны таким образом, чтобы сохранялась неотрицательность параметров и выполнялось неравенство ![]() . Для каждого набора мы вычисляли
. Для каждого набора мы вычисляли ![]() , используя (5) и находили значения
, используя (5) и находили значения ![]() , которое минимизирует g0(Q), используя функцию fmin из библиотеки scipy.optimize для языка программирования Python.
, которое минимизирует g0(Q), используя функцию fmin из библиотеки scipy.optimize для языка программирования Python.
4.2. Численные результаты для эвристической ошибки.
Мы исследуем качество приближения, вычисляя относительную ошибку от использования ![]() в качестве эвристического решения (
в качестве эвристического решения (![]() ) для различных r.
) для различных r.
В таблице 1 указаны максимальные эвристические ошибки для нескольких значений r, а также доли наборов, относительная ошибка которых меньше заданного значения.
Таблица 1
Эвристическая ошибка
|
r=0.5 |
r=0.6 |
r=0.7 |
r=0.8 |
r=0.9 |
r=1 | |
|
Макс |
0,765 |
0,679 |
0,608 |
0,549 |
0,497 |
0,453 |
|
% < 0,001 |
0,061 |
0,057 |
0,039 |
0,039 |
0,04 |
0,045 |
|
% < 0,01 |
0,284 |
0,28 |
0,28 |
0,271 |
0,266 |
0,274 |
|
% < 0,02 |
0,411 |
0,41 |
0,403 |
0,417 |
0,424 |
0,432 |
|
% < 0,05 |
0,613 |
0,627 |
0,631 |
0,64 |
0,642 |
0,65 |
|
% < 0,1 |
0,757 |
0,772 |
0,787 |
0,799 |
0,805 |
0,819 |
Как видно из таблицы, наименьшая относительная максимальная ошибка достигается при r=1, также при r=1 доля наборов, относительная ошибка которых меньше заданного значения, зачастую больше. Следовательно, можно сделать вывод, что в большей части случаев использование параметра r=1 является оптимальным. Также мы видим, что относительная эвристическая ошибка довольно низкая, из чего ясно, что возможно использование приближенной модели (3)-(5) вместо модели (1)-(2).
5. Заключение
В ходе исследования на численном эксперименте было установлено, что приближенная модель (3)-(5) может применяться вместо модели (1)-(2).
Преимущество приближенной модели в том, что можно найти решение в аналитической форме, что позволяет исследователям находить аналитические результаты, недостижимые для моделей, которые могут быть решено только с помощью численным методов.
Литература:
- Berk E., Arreola-Risa A. Note on “Future supply uncertainty in EOQ models” // Naval Res. Logist, 1994. Vol. 41, No.1. P.129–132.
- Parlar M., Berkin D. Future supply uncertainty in EOQ models // Naval Res. Logist., 1991. Vol. 38, No 1. P. 107–121.
- Parlar M., Perry D. Analysis of a (Q, r, T) inventory policy with deterministic and random yields when future supply is uncertain // Eur. J. Oper. Res., 1995. Vol. 84, No 2. P. 431–443.
- Parlar M., Perry D. Inventory models of future supply uncertainty with single and multiple suppliers // Naval Res. Logist., 1996. Vol. 43, No 2. P. 191–210.
- Snyder L. V., 2014. A tight approximation for an EOQ model with supply disruptions // Int. J. Production Economics., 2014. Vol. 155, P. 91–108.
- Tomlin B. T. On the value of mitigation and contingency strategies for managing supply chain disruption risks // Manag. Sci., 2006. Vol. 52, No 5. P. 639–657.

