В данной работе рассматривается решение обратной задачи динамики кинематических цепей. Предполагается что тела соединены произвольными вращательными сочленениями. Важным аспектом повествования является использование тензорной формы механики, основанной на работах Жилина П. А. В результате работы получены замкнутые аналитические выражения сил и моментов.

Ключевые слова: кинематические цепи, робототехника, обратная задача динамики, кинематика цепей, динамика цепей, тензорное исчисление, прямая задача кинематики.

Введение

При построении сложных робототехнических систем приходится решать ряд задач планирования движения и расчета динамики конкретного механизма. При этом обычно строится желаемое движение механизма, затем определяются силы и моменты, которые необходимы для реализации заданного движения, после чего выводятся уравнения движения. В реальном устройстве, с использованием уравнений движения и требуемого распределения сил и моментов, система стабилизируется около рабочей траектории. При этом должна быть решена задача нахождения сил, так же известная как обратная задача динамики. В данной работе рассмотрено решение данной задачи в приложении к кинематическим цепям абсолютно твердых тел со вращательными сочленениями. Важным аспектом повествования является применение тензорного исчисления в приложении к теоретической механике на основе работ Жилина П. А.

Кинематика цепей тел

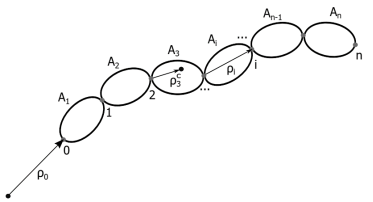
Рис. 1. Схематичный вид кинематической цепи.

Многие механизмы могут быть представлены как соединения звеньев, которые приближаются абсолютно твердыми телами. В свою очередь базовым является механизм из последовательно соединенных звеньев. Рассмотрим кинематику подобной цепи. Введем следующие обозначения:

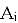1.                — i-e звено цепи (абсолютно твердое тело),
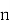2.                — длинна кинематической цепи (количество тел, ),
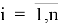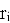3.                — вектор положения 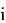-го сочленения (неподвижной точки соединения),
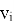4.                — скорость 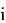-го сочленения (неподвижной точки соединения),
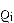5.                — вектор положения сочленения 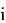относительно 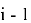, при этом 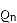выбирается произвольно,
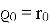6.                — вектор положения начала кинематической цепи,
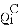7.                — вектор центра масс тела i относительно i-го сочленения,
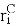8.                — вектор положения центра масс тела i,
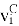9.                — вектор скорости центра масс тела i,
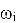10.           — угловая скорость i-го сочленения,
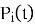11.           — тензор поворота (ориентации) i-го сочленения.

Предположим, что тензоры ориентации звеньев кинематической цепи выражаются последовательными поворотами: . Тогда, в соответствии с теоремой сложения угловых скоростей в тензорном виде [5, 6], запишем угловую скорость звена : , где  — угловая скорость поворота (здесь и далее  — операция нахождения векторного инварианта тензора [4, 7]). В соответствии с теоремой Эйлера [2, 3] можем записать линейную скорость произвольного сочленения: . Найдем теперь угловое ускорение звена : 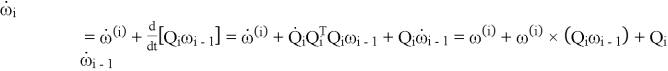. В соответствии с распределением ускорений в твердом теле [2, 3] запишем ускорение сочленения : Аналогично для скоростей и ускорений центра масс тела : , . Таким образом найдены все необходимые скорости и ускорения звеньев цепи, выраженные через характеристики относительных поворотов .

Производные динамических характеристик

Пусть тензоры инерции твердых тел заданы относительно центра масс. , где  — тензор инерции -го тела в отсчетный момент времени, а  — в текущий.  — количество движения -го тела цепи,  — кинетический момент тела относительно центра масс. Тогда:

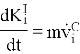
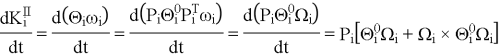
 — правый вектор угловой скорости.

Силы и моменты в кинематической цепи

Рассмотрим движение -го тела кинематической цепи, пусть тело цепи действует на тело силой , тогда со стороны предыдущего тела действует сила , теперь можем записать силу, с которой окружение действует на тело:

Соответственно рассмотрим момент относительно центра масс, действующий на тело :

 (1)

Известно, что любой момент может быть записан в следующем виде:

Здесь  — произвольная точка, называемая точкой приведения. При этом, если тело не сопротивляется поворотам около точки вокруг какой-либо оси , то проекция на эту ось равна нулю. Разложим таким образом все члены в правой части (1), выбирая в качестве точки приведения неподвижную точку соответствующего соединения, а для силы тяжести — центр масс тела.

.

Введем обозначения , учтем определение вектора и , тогда выражение примет вид:

Теперь можем составить уравнения баланса кинетического момента и уравнение баланса количества движения для каждого звена на основе теорем об изменении количества движения и кинетического момента твердого тела [1, 3].

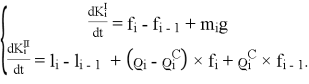 (2)

Таким образом выведены динамические уравнения, которые с одной стороны позволяют приступить к решению обратной задачи динамики, а с другой стороны — вывести дифференциальные уравнения движения цепи в обобщенных координатах (для этого требуется параметризировать все тензоры ориентации обобщенными координатами).

Обратная задача динамики кинематической цепи

Рассмотрим систему (2), неизвестными в ней выступают вектора , при этом имеется всего векторных уравнений, линейных относительно неизвестных. Таким образом решение системы (2) выражается через два векторных параметра. Для решения неоднозначности выберем в качестве параметров вектора и найдем вид решения.

Теорема. Пусть задано движение кинематической цепи. Допустим, например, что в любой момент времени известны следующие характеристики:

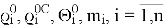1.                — константы кинематической цепи (вектора относительных положений сочленений, центров масс, тензоры инерции и массы звеньев в отсчетный момент времени),
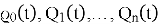2.                — определяющие движения (вектор положения начала цепи и тензоры последовательных поворотов звеньев).

Тогда силы и моменты однозначно выражаются через вектора То есть решение обратной задачи динамики является двупараметрическим семейством сил и моментов векторных параметров.

Доказательство. Докажем теорему конструктивно. Для начала будем идти по возрастающему индексу .

Прямой проход:

Исходя из описанной кинематики, последовательно для находим:

1.               ,
2.               ,
3.               ,
4.               ,
5.               ,
6.              
7.               ,
8.               ,
9.               ,
10.          ,
11.          ,
12.          ,
13.          .

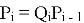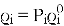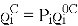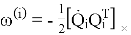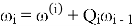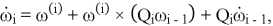
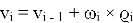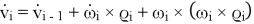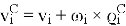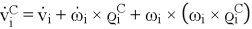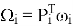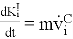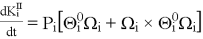Обратный проход:

Используя (2) вычисляем силы, действующие в сочленениях для :

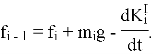
И, аналогично, опираясь на второе равенство в системе (2), моменты в сочленениях:

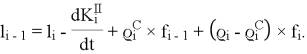
Раскрывая итеративные равенства, окончательно получаем:

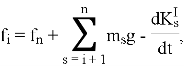
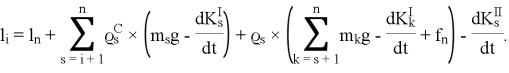
(3)

В силу однозначности всех выполненных операций — решение единственно при заданных векторных параметрах. Таким образом теорема полностью доказана, а решение — найдено.

Решение для цепи со свободным концом

Конец цепи называется свободным, если для него выполняются условия . При этом однозначно определено решение обратной задачи, в частности, если цепь закреплена начальным концом на основании, то реакция опоры так же определена. Вид решений можно получить если подставить в (3) условие .

Заключение

В работе использован аппарат тензорного исчисления, с помощью которого описана кинематика и динамика цепных механизмов. Также приведено подробное изложение процесса нахождения сил в системе. Таким образом, основным результатом работы является (3) — решение в явном виде обратной задачи динамики кинематической цепи с произвольными вращательными сочленениями. С другой стороны, полученные выражения могут быть использованы для записи уравнений движения в обобщенных координатах. Для этого достаточно рассматривать правые части указанных уравнений как параметризованные обобщенными координатами и учесть оси вращения сочленений.

Литература:

1.               Пупышева Ю. Ю., Бабаджанянц Л., К., Пупышев Ю. А. Классическая механика. Издательство Санкт-Петербургского Университета, 2011.
2.               Королев В. С., Потоцкая И. Ю., Ермолин В. С. Теоретическая механика. Кинематика. ВВМ СПбГУ, 2012.
3.               Королев В. С., Потоцкая И. Ю., Ермолин В. С. Теоретическая механика. Динамика. ВВМ СПбГУ, 2013.
4.               Вильчевская Е. Н. Тензорная алгебра и тензорный анализ. СПб.: Издательство Политехнического Университета, 2012.
5.               Жилин П. А. Векторы и тензоры второго ранга в трехмерном пространстве. СПбГПУ, 2012.
6.               Жилин П. А. Динамика твердого тела. СПбГПУ, 2014.
7.               Leonid Lebedev, M. J. Cloud, and Victor Eremeyev. Tensor analysis with applications in mechanics, 2nd edition. World Scientific Pub Co Inc, 2010.