Опыт преподавания математики студентам гуманитарных специальностей

Автор данной публикации на протяжении нескольких лет преподает высшую математику студентам Санкт–Петербургского государственного университета технологии и дизайна. При этом на занятиях периодически слышится вопрос: «Зачем же нам нужна эта математика?» К сожалению, многие из студентов, обучающихся в данном ВУЗе, вспоминают школьную математику как страшный сон и имеют за ЕГЭ по математике ниже 45 баллов. Большинство прошедших передо мной студентов обучались по специальностям «Экономика», «Химия», «Туризм», «Менеджмент», и выбор будущей специальности, по их признанию, в частности, объяснялся надеждой на малое присутствие математики в учебной программе. Средний студент приходит после школы на первый курс с неусвоенными элементарными математическими понятиями. Это лишний раз подтверждает неблагополучную ситуацию, которая сложилась в современном российском образовании.

Прослеживается тенденция занижения математического образования в средних школах. С. М. Никольский в статье «О математике в общеобразовательных школах» приводит следующие данные: «По школьным учебным планам выделялось на арифметику и алгебру (ранее в 4–8 классах, теперь в 5–9 классах) в 1949 г. — 900 часов, в 1975–800, в 1999–650, уменьшение на 27 %» [1, с. 117].

Урон качеству математического образования наносится и введением Единого Государственного Экзамена. Так как успешность работы учителя оценивается результатами, полученными при прохождении его учениками ЕГЭ, то учащихся в 11 классе фактически только «натаскивают» на решение стандартных заданий, при этом большинство школ ставят своей задачей только разбор заданий части В, ограничиваясь пассивным заучиванием алгоритмов решения. Введение еще одного тестового экзамена после 9 класса только ухудшило ситуацию.

В книге Peter Sacks «Standardized Minds: the high price of America's testing culture and what we can do to change it». [2] производится анализ тестовой системы и делается вывод, что она формирует стандартное мышление. Тогда как первоначальная идея экзамена состоит в том, чтобы увидеть, как молодой человек мыслит, тест проверяет, способен ли ученик хранить в памяти большой объем зазубренной информации. «При такой системе выигрывает тот, кто имеет клочные, надерганные, случайные знания — и отсеиваются именно талантливые, логичные, люди самостоятельного ума», — говорил А. И. Солженицын в интервью телевизионной программе «Вести недели» [3].

В итоге студенты, которых набирают на первый курс, приходят в университет совершенно неподготовленными к дальнейшему обучению и усвоению материала. Приходится тратить время на повторение элементарных основ математики, например, заново учиться складывать дроби.

В связи с низким уровнем подготовки учащихся, недостатком аудиторного времени на полноценное прохождение курса математики и отсутствием простой и доступной литературы по высшей математике, которую можно посоветовать студентам для самостоятельной работы, мною было разработано электронное учебное пособие.

Конспект имеет практическую направленность. Материал изложен в максимально подробной форме, чтобы с ним могли работать студенты с изначально низким уровнем (пособие апробировано на студентах с баллами ЕГЭ по математике около 23–28). С помощью данного учебного пособия студенты могли разобраться с конкретными непонятными моментами и наиболее сложными задачами, которые не были усвоены во время аудиторного занятия; самостоятельно изучить тему в случае пропуска занятия.

Конспект содержит в себе полный материал аудиторного практического занятия. Также в него включены дополнительно разобранные задачи, которые не были решены во время работы в классе. В конце каждой темы приведено домашнее задание, к каждому примеру приложен ответ для самоконтроля. Благодаря этому студентам не приходится переписывать задания с доски, экономится время занятия и исключены описки. Конспект содержит в себе самую необходимую информацию по каждой из пройденных тем, включая теоретический минимум, базовые понятия.

Разобранные примеры взяты из различных задачников по высшей математике, которые используются на занятиях на кафедре математики, либо придуманы самостоятельно, так как в задачниках не всегда получается найти задание, необходимое для отработки конкретного навыка.

По электронным конспектам студенты без всяких затруднений смогли подготовиться к досрочному письменному экзамену по высшей математике. Им не пришлось искать дополнительную литературу и тратить на это время, весь необходимый материал уже был собран в одном месте.

Статистика результатов сдачи досрочного письменного экзамена моими студентами, 21 человек:

«отлично»: 66,68 %;

«хорошо»: 14,28 %;

«удовлетворительно»: 14,28 %;

«неудовлетворительно»: 4,76 %.

Мотивацией при создании данных конспектов послужило отсутствие единого учебного пособия, в котором можно найти все темы и нужные задачи. При подготовке к занятиям приходится ознакомиться с большим количеством литературы, продумывать, как изложить материал в простой и понятной форме, подбирать и прорешивать подходящие примеры. Тратится значительное количество времени на подготовку. Конспекты служат первой попыткой систематизации накопленного преподавательского опыта автора и создания единого простого доступного пособия по высшей математике для студентов-гуманитариев.

Разработанное учебное пособие полностью удовлетворяет требованиям к содержанию учебника: научность, наглядность, системность изложения учебного материала, доступность, обеспечение предметных результатов.

Ниже приведена часть конспекта по теме «Решение системы линейных алгебраических уравнений методом последовательного исключения переменных».

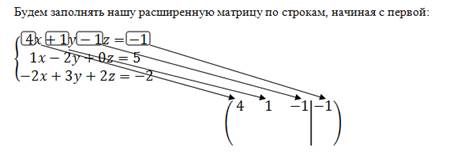
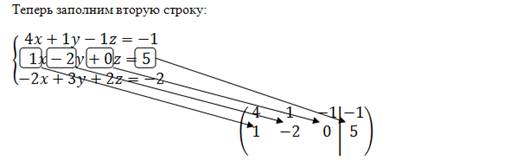
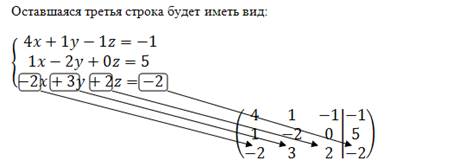
С глубокой древности математическое образование является частью общечеловеческой культуры. Любому человеку в современном мире необходимо уметь мыслить, необходима способность к самостоятельной интеллектуальной деятельности. Доказано, что математика является эффективным средством развития культуры мышления. Мерой мыслительных способностей является способность к абстрагированию. Особая ответственность за формирование абстрактного мышления лежит именно на математике. Кроме того, математика — это база, способствующая возможности самообразования, обеспечивающая готовность к овладению другими дисциплинами. Например, студенты экономических специальностей после изучения математики могут приступить к курсу «Математические методы в экономике».

Успех большинства людей зависит от уровня их умственных и творческих способностей, развитию которых помогает математика.

Литература:

1.                  С. М. Никольский. О математике в общеобразовательных школах. Сборник статей «Образование, которое мы можем потерять». Под общей редакцией ректора МГУ им. М. В. Ломоносова академика В. А. Садовничего. М: МГУ им. Ломоносова, 2003.

2.                  Peter Sacks. Standardized Minds: the high price of America's testing culture and what we can do to change it. USA, NY: Da Capo Press, 2000.

3.                  А. И. Солженицын. Школьников учат по неправильным учебникам. Интервью телевизионной программе «Вести недели». Выпуск от 16.09.2001. http://www.vesti7.ru/archive/news?id=429