Применение 3D-моделирования для изучения наглядной геометрии



Ум ребенка находится на кончиках его пальцев.

В. Сухомлинский

В связи с принятием в мае 2021 года обновленных федеральных государственных образовательных стандартов основного общего образования (далее — ФГОС ООО) в содержании математического образования в 5–9-х классах произошли изменения, направленные на реализацию Концепции развития математического образования в Российской Федерации (утверждена в 2013 г.) и выполнение поручения Президента РФ «обеспечить совершенствование преподавания учебных предметов «математика» и «информатика» в общеобразовательных организациях, установив их приоритет в учебном плане и скорректировав содержание примерных основных образовательных программ общего образования» (декабрь 2020 г.).

Написано, что личностные результаты освоения программы по математике в части эстетического воспитания должны отражать «способность к эмоциональному и эстетическому восприятию математических объектов, задач, решений, рассуждений; умение видеть математические закономерности в искусстве». А метапредметные результаты освоения программы регулятивного характера в части самоорганизации должны обеспечивать формирование следующих умений: «самостоятельно составлять план, алгоритм решения задачи, выбирать способ решения с учетом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учетом новой информации» [4].

Есть в программе математики 5 класса особый раздел, которого педагог ждет с нетерпением, так как это встреча с очень красивым материалом- разделом «Наглядная геометрия. Тела и фигуры в пространстве», в котором изучаются различные многогранники, их свойства.

Человек проявляет интерес к многогранникам на протяжении всей своей жизни — от ребенка, играющего деревянными кубиками, до зрелого человека.

До изучения темы «Модели пространственных тел» на математике с учащимися рассматриваются развертки куба и параллелепипеда, решаются некоторые задачи на вычисления их площадей, объёмов. И уместно подвести итог изученного материала уроком-исследованием, в котором выполняются две практические работы с обоснованием некоторых гипотез.

Цель исследовательской работы № 1: С использованием 3D моделирования и исследования доказать или опровергнуть гипотезу: действительно ли существует зависимость объёма куба от длины его ребра.

Задачи работы:

1. Разработать алгоритм моделирования соединительных элементов в САПР Компас-3D.
2. Напечатать соединительные элементы моделей на 3D принтере, собрать каркасные модели кубов.
3. Изучить свойства кубов, провести вычисления с занесением данных в таблицу.

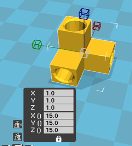
Для доказательства гипотезы необходима предварительная работа по моделированию в программе Компас 3D соединительных элементов каркасных тел.

Алгоритм моделирования:

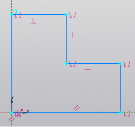
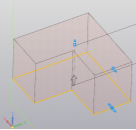
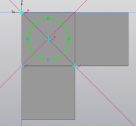
1. Построить эскиз, выдавить его на 7,5 мм (рис.1, 2);
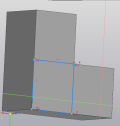
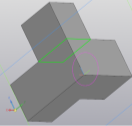
2. Вернуться в режим эскиза, в центральной части начертить квадрат со стороной 7,5 мм, выдавить на 7,5 мм (рис. 3, 4);
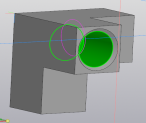
3. Начертить окружность диаметром 5,8 мм, вырезать её на 7,5 мм (рис. 5, 6).
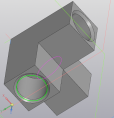
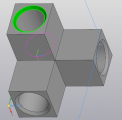
4. На других сторонах повторить построение окружности и вырезание. Сделать фаски по 0,5 мм (рис. 7, 8).

1.	2.	3.	4.
5.	6.	7.	8.

Напечатанные PLA-пластиком соединительные элементы каркасных тел используются группой учеников, отвечающих за сборку каркасных моделей. В качестве рёбер используются трубочки для флажков и воздушных шаров.

После сборки моделей, учащиеся изучают их свойства, проводят вычисления и заносят данные в таблицу в 5, 6 строки. Класс тем временем, проводит измерения, вычисления своих картонных моделей с занесением данных в таблицу в 1–4 строки. Итоговые данные 1–4 строки проверяются, при проверке 5,6 строк группа учеников, отвечающая за каркасные модели, показывает наглядно на моделях, что при увеличении ребра в 2 раза в большой куб помещается 8 меньших кубов:

	Размеры кубов	Длина ребра (а)	Расчёт объёма куба	Объём куба (куб.см)	Vб:Vм
1	Куб 3х3х3см	3	V1=3х3х3=27	27	8
2	Куб 6х6х6см	6	V2=6х6х6=216	216
3	Куб 2х2х2см	2	V3=2х2х2=8	8	27
4	Куб 6х6х6см	6	V4=6х6х6=216	216
5	Куб меньший	13	V5=13х13х13=2197	2197	8
6	Куб больший	26	V6=26х26х26=17576	17576

Из исследования делается вывод: если ребро а первого куба увеличить в N раз, то ребро второго куба будет равно N а . Тогда объем первого куба V ₁ =а·а·а= а ³ , а объем второго куба V ₂ =Nа·Nа·Nа=(Nа) ³ = N ³ ·a ³ .

Т. е. объем куба увеличится в N ³ раз. То есть гипотеза доказана: существует зависимость объёма куба от длины его ребра.

Цель исследовательской работы № 2:

Обосновать, доказать гипотезу: действительно ли в любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2, т. е. Г + В — Р = 2 (Т. Эйлера).

Задачи работы:

1. Подготовить презентацию, заслушать доклад по теме «Правильные многогранники».
2. Создать многогранники (из картона, из пластика: смоделировать многогранники в программе Компас 3D, напечатать их на 3D принтере; использовать 3D ручки).
3. Изучить, подсчитать и записать в таблицу количество элементов многогранников.

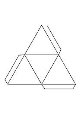
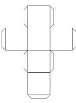
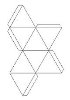
Для доказательства гипотезы необходима предварительная работа по созданию развёрток правильных многогранников из картона: на уроке многогранники склеивают, изучают свойства, делают подсчёты, данные заносят в таблицу.

тетраэдр	гексаэдр	октаэдр	додекаэдр	икосаэдр

Также пространственные тела можно создать с помощью 3D ручек.

И смоделировать в программе Компас 3D, потом распечатать с помощью 3D-принтера.

Ученики используют результаты своей деятельности — созданные модели, делают расчёты, фиксируют результаты вычислений в таблицу. Результат работы:

Правильный многогранник		Элементы многогранников			Г+В-Р
		Число граней (Г)	Число вершин (В)	Число ребер (Р)
Тетраэдр		4	4	6	2
Куб (Гексаэдр)		6	8	12	2
Октаэдр		8	6	12	2
Додекаэдр		12	20	30	2
Икосаэдр		20	12	30	2

Из исследования делается вывод: в любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2 (Г + В — Р = 2), то есть гипотеза доказана.

В результате проведенного урока-исследования получены новые теоретические, практические знания и навыки в области информационных технологий и математики: проанализированы свойства различных видов правильных многогранников и подтверждены гипотезы, рассмотрены методы построения соединительных элементов каркасных тел, многогранников с помощью САПР Компас 3D, улучшены навыки пространственного видения, мышления.Начала работать выставка «Развитие пространственного мышления».

Литература:

1. ЗАО Аскон Азбука Компас 3D. Учебное пособие. — АСКОН, КОМПАС, 2020
2. Баранова, И. В. КОМПАС-3D для школьников. Черчение и компьютерная графика. — М.: ДМК Пресс, 2018
3. http://veselowa.ru/urok-12-byistroe-sozdanie-3d-modeli-po-2d-eskizu/3. http://veselowa.ru/urok-12-byistroe-sozdanie-3d-modeli-po-2d-eskizu/
4. Примерная основная образовательная программа основного общего образования (одобрена решением федерального учебно-методического объединения по общему образованию, протокол от 18.03.2022 N 1/22)