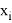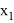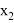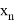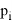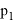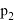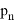Теория вероятностей и математическая статистика в школьной программе: вчера, сегодня, завтра
Автор: Никонов Максим Викторович
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
XXVI международная научная конференция «Педагогическое мастерство» (Казань, апрель 2022)
Дата публикации: 02.04.2022
Статья просмотрена: 446 раз
Библиографическое описание:
Никонов, М. В. Теория вероятностей и математическая статистика в школьной программе: вчера, сегодня, завтра / М. В. Никонов. — Текст : непосредственный // Педагогическое мастерство : материалы XXVI Междунар. науч. конф. (г. Казань, апрель 2022 г.). — Казань : Молодой ученый, 2022. — С. 20-25. — URL: https://moluch.ru/conf/ped/archive/434/17075/ (дата обращения: 23.04.2024).
В статье автор рассматривает современные программы образования в области в математики, в одной из важнейших тем — теории вероятностей, предлагая новые методы в изучении основных моментов дисциплины.
Ключевые слова: теория вероятностей, школьное образование.
Одним из важнейших разделов школьной математики является теория вероятностей, которая является основополагающим инструментом для Data Science, моделирования, предсказания, теории рисков, а также других межпредметных дисциплин с химией, физикой и не только. Поэтому знания теории вероятностей даже на школьном уровне является важным фактором научного и практического развития человека в целом.
На данный момент весь курс теории вероятностей сводится к комбинаторике и некоторым теоремам о том, что такое вероятность. Принято упрощать, не говоря о вероятностном пространстве, опуская определение случайной величины, функций распределения и не только. Так определение вероятности дается следующее: если опыт, в котором появляется событие A, имеет конечное число n равновозможных исходов, то вероятность события А равна: P(A) = m / n, где m — число благоприятных исходов, а n — число всех возможных исходов. Эту тенденцию можно проследить от учебника к учебнику, например в таких российских учебниках, как «Алгебра и начала математического анализа. 10–11 классы» под авторством Шабунина, Алимова и др [1], «Алгебра и начала математического анализа. 10 класс. Базовый и углубленный уровень. Дидактические материалы. Пособие для общеобразовательных организаций» под авторством Михаила Потапова, Александра Шевкина [2] и множества других книг, по которым обучаются в средних общеобразовательных школах.
Если обратиться к истории появления теории вероятностей, то можно понять, что определение случайной величины было изначально. Рассматривались случайные величины на примере азартных игр. Тем не менее на данный момент ни один школьный учебник не имеет этого определения, что является существенно неверным упрощением для этого курса, поскольку все зародилось из этого определения. Конечно, строгое определение [3] сложно воспринимать со школьными знаниями. Однако можно переформулировать это и другими словами, например ввести такое определение: случайная величина — это численная переменная, которая принимает свои значения в зависимости от случайных обстоятельств. Такое упрощение имеет место, если мы сделаем некоторые уточнения: случайная величина бывает двух типов — дискретная и непрерывная. Дискретная принимает отдельные числовые значения. Примером такой случайной величины может послужить значения, которые мы получаем при подкидывании игральной кости. Непрерывная принимает любые значения из некоторого интервала. Примером такой случайной величины может послужить масса тела человека или рост студентов. Для случайной величины нужно ввести некоторый закон, поскольку, даже будучи студентом, понимания о том, что случайности не случайны, не приходит. Тогда мы можем привести в пример некоторое представление в виде таблицы 1, опираясь на школьное понятие вероятности:
Таблица 1
Представление закона в виде таблицы
|
|
|
|
… |
|
|
|
|
|
… |
|
Где
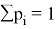
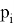
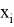
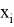
Возвращаясь к истории становления теории вероятностей, необходимо задать функцию распределения, как то, что породило многочисленные проверки данных на схожесть с распределением и теоремы, необходимые для анализа данных и многих методов машинного обучения.
Примером, наглядно иллюстрирующем нормальное распределение, необходимо выбрать доску Гамильтона [4], проиллюстрированной на рис. 1.
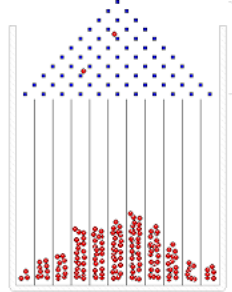
Рис. 1. Доска Гамильтона
Нормальным оно было названо, в частности, по причине того, что часто наблюдается в физических процессах. Суть этого изобретения в том, что шарик может с одинаковой вероятностью перейти в левую или правую сторону, то есть случайно, однако то, как расположены шарики, в среднем описывают одну и ту же фигуру, что наталкивает на мысль о том, что случайность на самом деле не случайна. Наглядно принцип работы этого изобретения покажем на рис. 2.
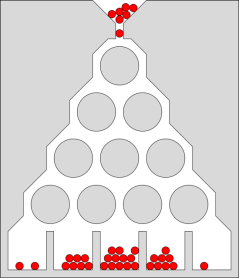
Рис. 2. Доска Гамильтона
Отталкиваясь от уже показанного распределения, необходимо отметить, что существует еще огромное число разных распределений, отраженных на рис. 3.
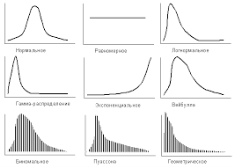
Рис. 3. Другие виды распределений
Таким образом, не сильно усложняя программу, опираясь только на те знания, которые есть в курсе теории вероятностей, можно перейти и к изучению вопросов нахождения аномалий (или выбросов), визуальной проверке данных на нормальность с помощью квантиль-квантиль графиков, то есть на то, на сколько распределение данных похоже на нормальное, численное нахождение и моделирование с помощью средств ЭВМ, связи распределения и вероятности и не только. Поскольку нахождение вероятности из функции распределения является задачей решения интеграла Стилтьеса [5], его следует давать уже в 10–11 классе, когда ученики смогут его считать. Моделирование случайных величин можно проходить вместе с основным курсом программирования, в рамках предмета Информатика. Такое, порой незначительное уточнение в одном разделе математики может побудить интерес ученика в ряде других наук, увеличит уровень межпредметности в целом.
Литература:
1. Ш. А. Алимов, Ю. М. Колягин, М. И Шабунин и др. Алгебра и начала математического анализа. 10–11 классы. — М. Просвещение, 2007
2. Никольский С. М., Потапов М. К., Решетников Н. Н. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. — М. УМК «МГУ — школе»
3. Случайная величина. URL: https://clck.ru/ehap6
4. Доска Гамильтона. URL: https://clck.ru/ehaou
5. Интеграл Римана — Стилтьеса. URL: https://clck.ru/ehaor