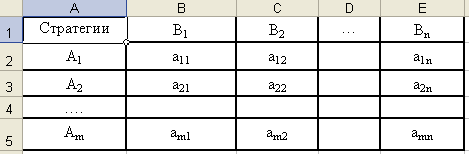
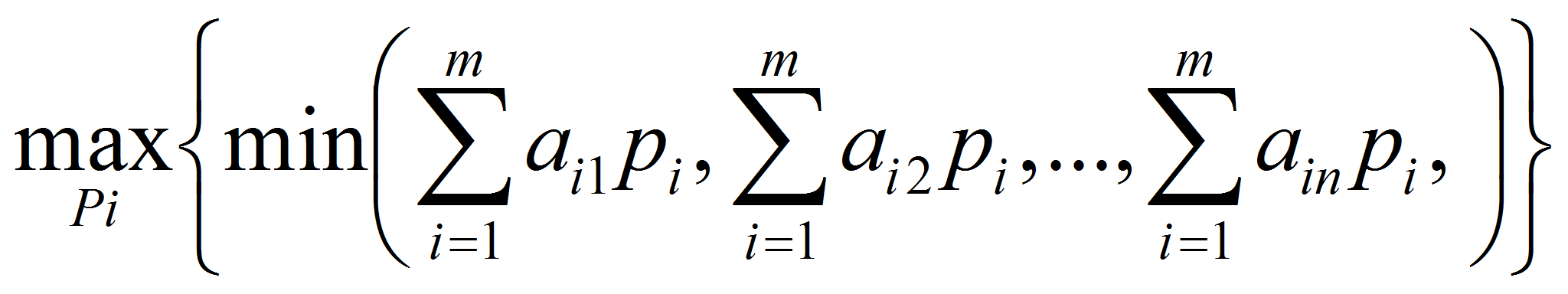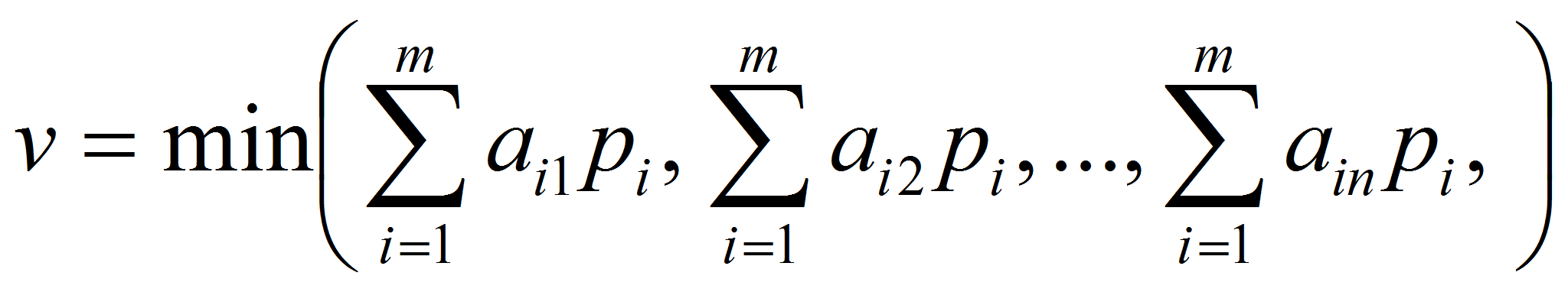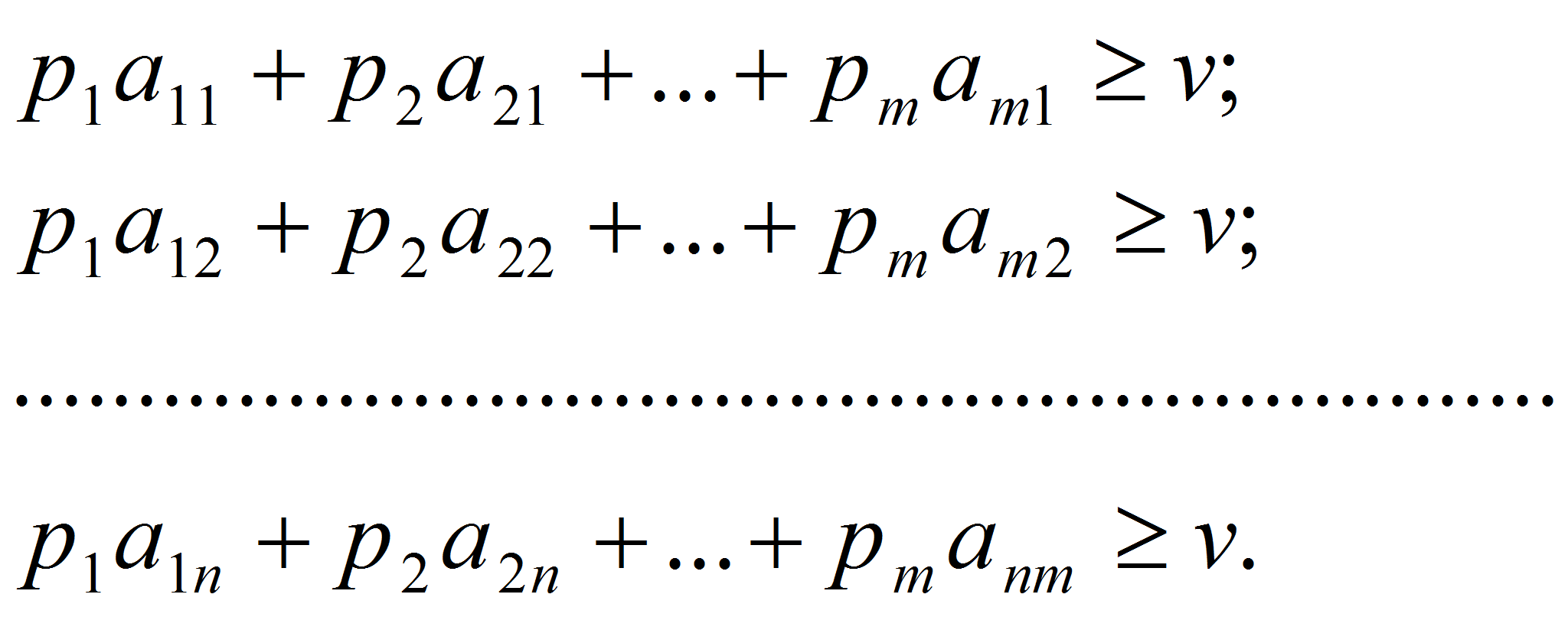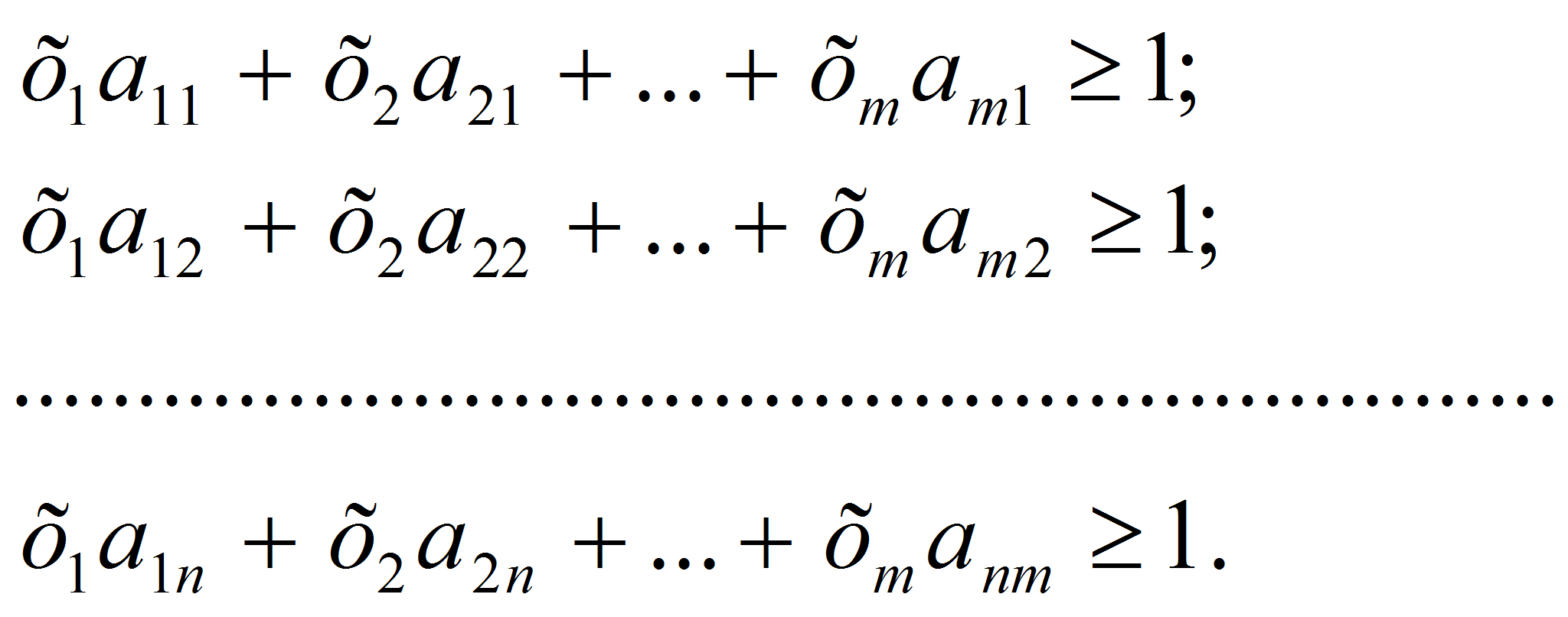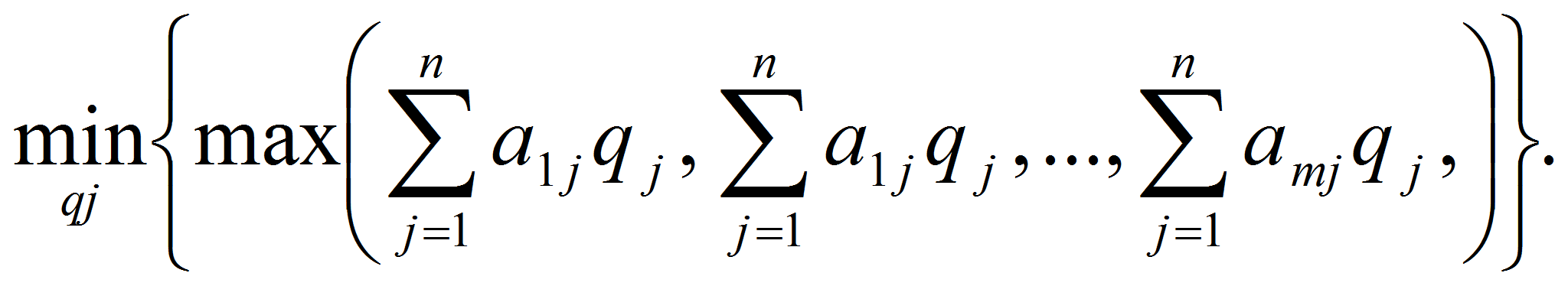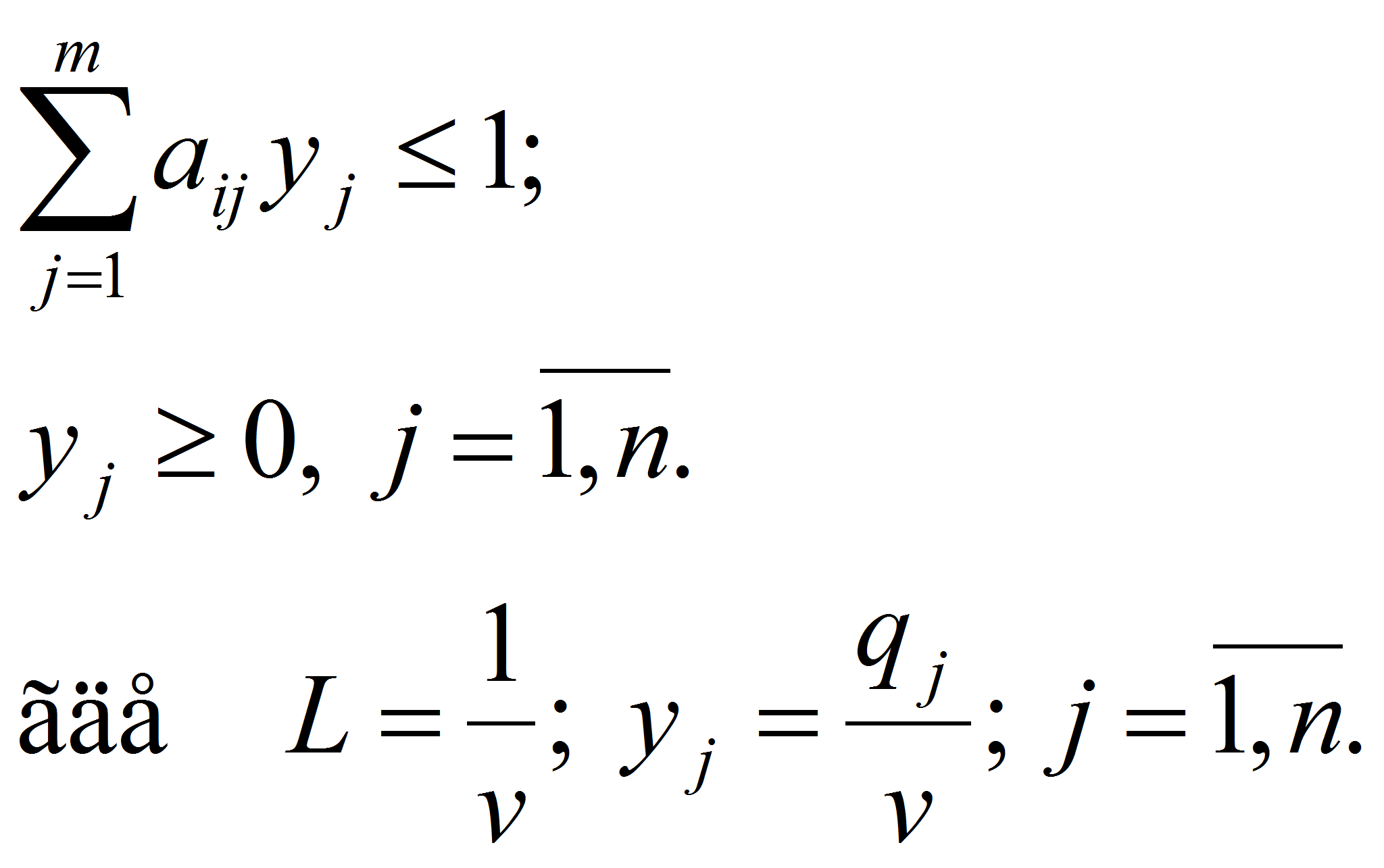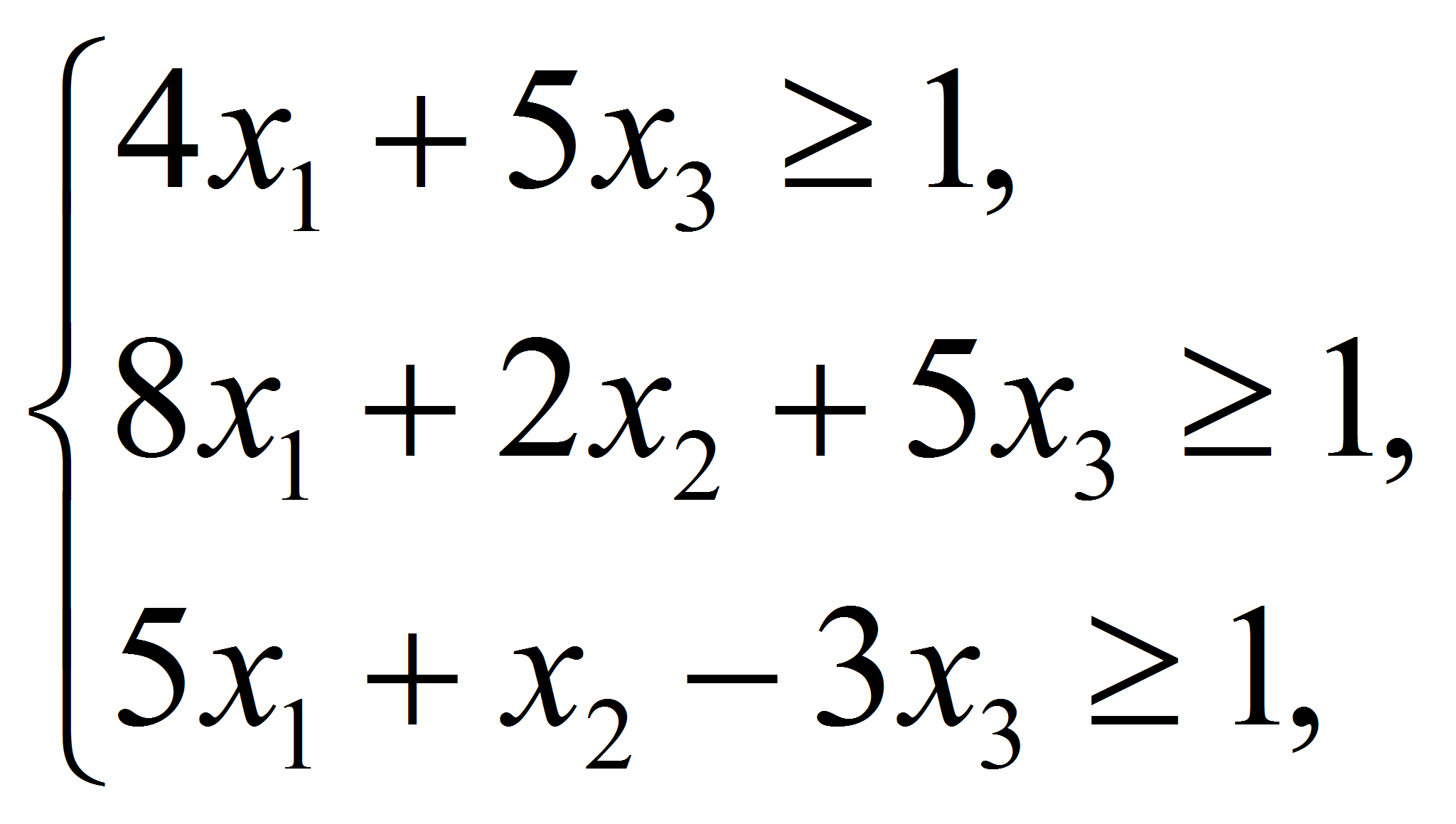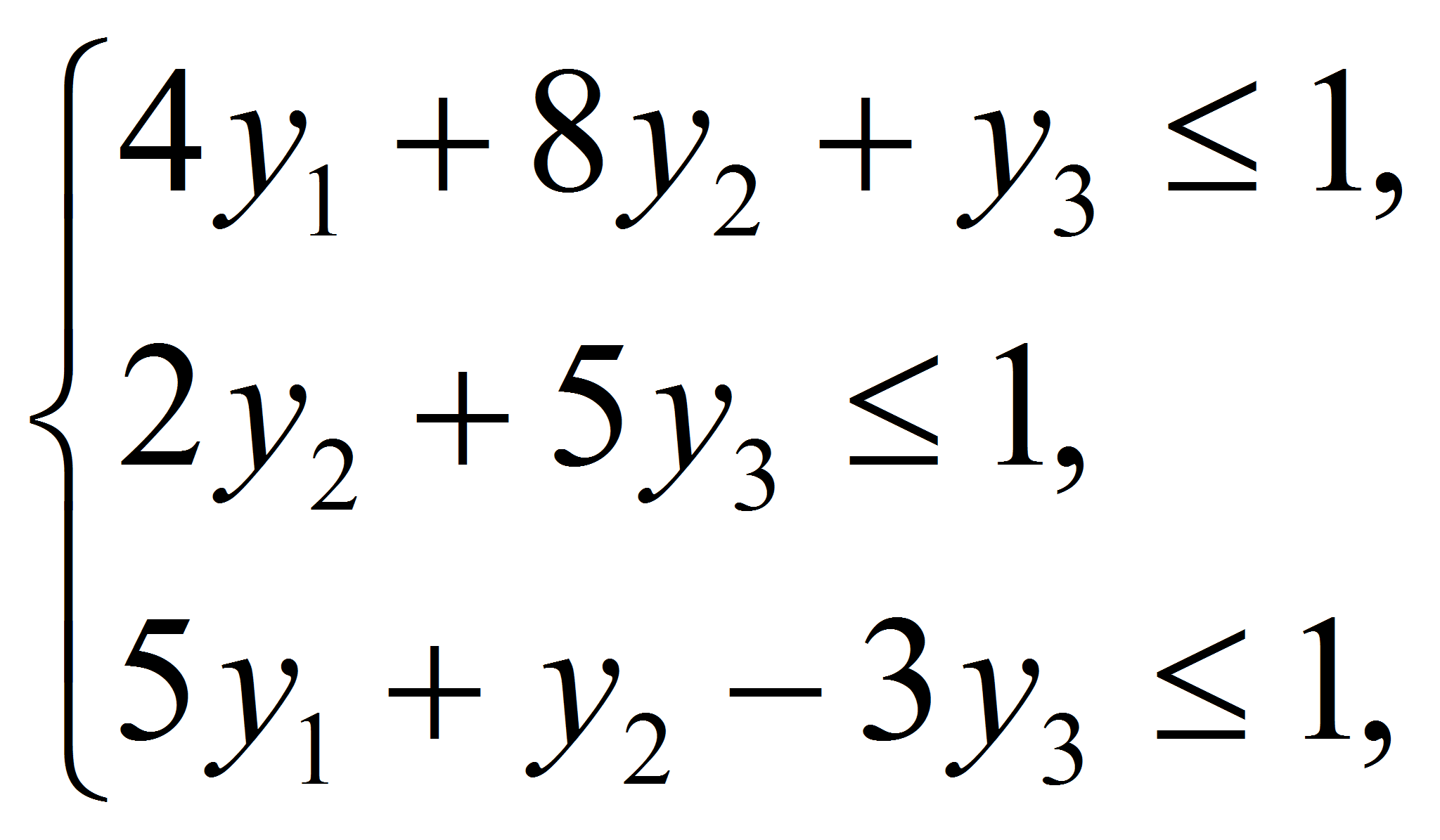Рассмотрим общий случай игровой задачи m x n с нулевой суммой, когда модель задачи не имеет седловой точки. Такую модель можно представить в виде матрицы (табл.1):
Таблица 1. Общая таблица стратегий
|
Стратегии |
В1 |
В2 |
… |
Вn |
|
A1 |
a11 |
a12 |
|
a1n |
|
A2 |
a21 |
a22 |
|
a2n |
|
…. |
|
|
|
|
|
Am |
am1 |
am2 |
|
amn |
Оптимальное
решение необходимо искать в области смешанных стратегий. Обозначим
вероятности применения стратегий первого игрока (игрока А) через
![]() ,
а цену игры — через v.
Оптимальная смешанная стратегия игрока А определяется из условия
,
а цену игры — через v.
Оптимальная смешанная стратегия игрока А определяется из условия
Пусть
Поскольку при оптимальной стратегии средний выигрыш не меньше v при любой стратегии противника, то справедлива система n неравенств:
Или
Тогда задача отыскания оптимальной смешанной стратегии игрока А может быть сформулирована в виде задачи линейного программирования.
Для этого необходимо максимизировать целевую функцию F =v при ограничениях
Введем новые неизвестные:
Разделим левую и правую части неравенств (1) и (2) на v, получим:
В силу того что
max v = min 1/v = min{x1+x2+…+xm}.
задача принимает вид
F= x1+x2+…+xm → min (4)
при ограничениях
Для второго игрока (игрока В) оптимальная стратегия определяется из условия:
при условии
q1+q2+…+qn = 1
Эта задача записывается как симметричная двойственная задача линейного программирования к задаче игрока A (4), (5):
L= y1 +y2+… +yn → max (6)
при ограничениях
Задачи игроков A и В решают симплекс-методом.
Использование возможностей Microsoft Excel позволяет существенно облегчить и ускорить решение этой задачи.
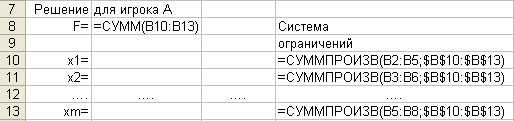
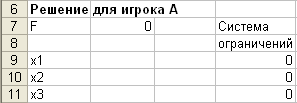
Сначала нужно создать исходную таблицу:
Затем, на основе этой таблицы записать формулы для нахождения решения:
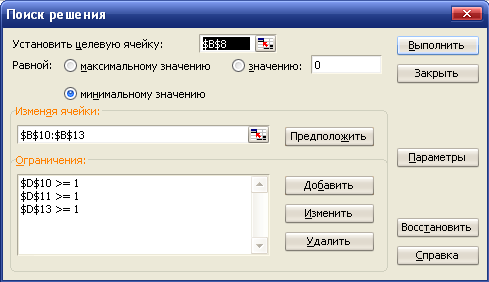
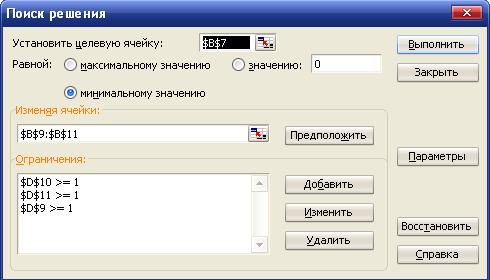
Для нахождения решения используется надстройка Поиск решения. Нужно выделить ячейку, в которой вычисляется значение функции F и вызвать надстройку Поиск решения. Заполнить окно поиска решения:
В поле Ограничения нужно задать формулы для всех ограничений. Затем нажать кнопку Параметры и отметить поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК, затем Выполнить.
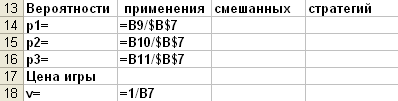
Чтобы найти значения вероятностей и цену игры нужно записать формулы:
Решение задачи для игрока В выполняется по аналогичной схеме согласно формулам (6), (7).
Рассмотрим пример
решения задачи. Найдем
решение игры, заданной матрицей
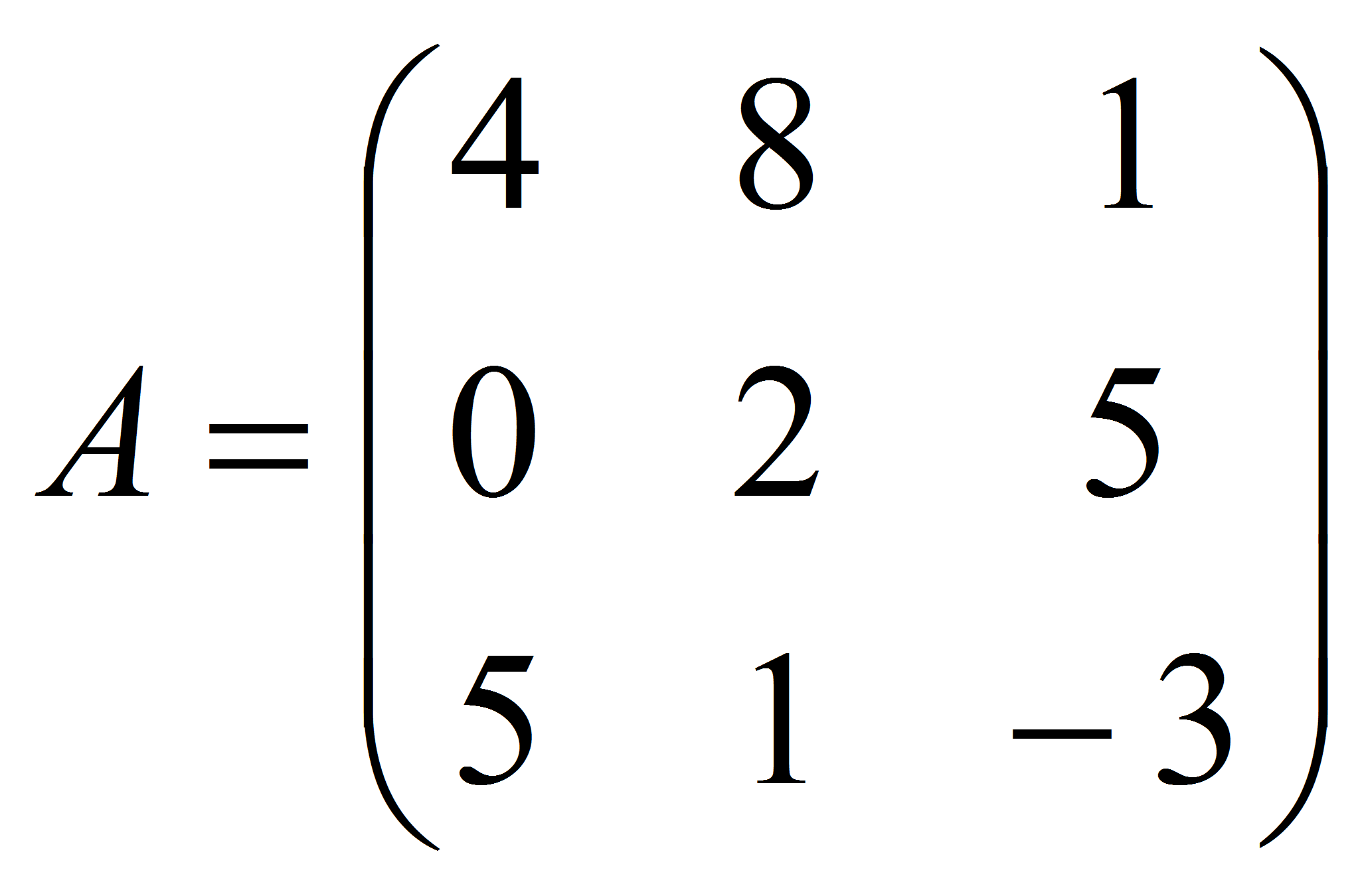 .
.
Проверим наличие седловой точки.
В режиме отображения формул эта запись имеет вид:
Поскольку нижняя цена игры (минимальный выигрыш игрока А) и верхняя цена игры (максимальный проигрыш игрока В) не равны, то модель данной задачи не имеет седловой точки. Поэтому решение следует искать в смешанных стратегиях. Составим задачи линейного программирования для нахождения решений игроков А (согласно формулам (4), (5)) и В(согласно формулам (6), (7)):
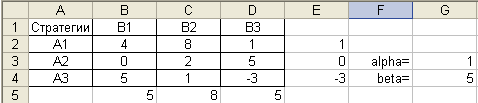
Для решения этих систем используем надстройку «Поиск решения». Сначала оформим задачу для поиска решения игрока А:
В режиме отображения формул:
Затем нужно активировать ячейку В7 и запустить надстройку Поиск решения. Далее заполнить окно Поиска решения:
Затем нажать кнопку Параметры и отметить поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК, затем Выполнить.
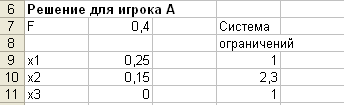
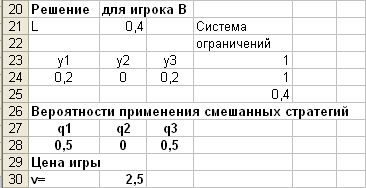
Получим результат:
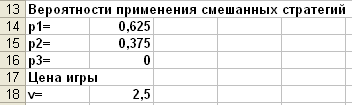
Вероятности применения смешанных стратегий и цену игры найдем по формулам: pi=xi/F, v=1/F.
В режиме отображения формул:
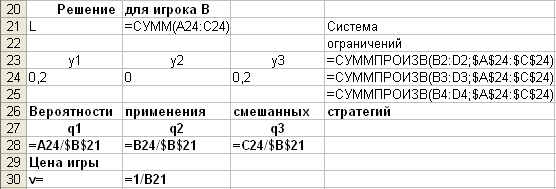
Аналогично найдем решение для игрока В:
В режиме отображения формул:
Литература:
1. Акулич И.Л. Математическое программирование в примерах и задачах. М. «Высшая школа», 1993г.
2. Агальцов В.П., Волдайская И.В. Математические методы в программировании М. ИД «Форум» - ИНФРА-М, 2006г.
3. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем М. «Финансы и статистика», 2003г.
4. Партыка Т.Л., Попов И.И. Математические методы М. ИД «Форум» - ИНФРА-М, 2007г.