Урок-моделирование во 2-м классе по теме: «Разнообразие фигур. Построение многоугольника»

 

Тип занятия: усвоение новых знаний.

Форма занятия: моделирование.

Цель:

Создать условия для формирования понятия «многоугольник»

Планируемые результаты:

           предметные: формировать умения различать, называть многоугольники; строить многоугольник из соответствующего количества палочек, соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами;

           метапредметные: формировать универсальные учебные действия:

           регулятивные: понимать, принимать и сохранять учебную задачу, осуществлять самоконтроль и самооценку;

           познавательные: формировать умение проводить сравнение, выстраивать цепочку логических рассуждений

           личностные: способствовать развитию интереса к математике

Оборудование:

•                   карточки:

         для индивидуальной работы,

         для работы в парах;

•                   счетные палочки; демонстрационный материал; игра “Танграм”;
•                   презентация

ХОД УРОКА

I. Оргмомент.

II. Разминка.

1. Индивидуальная работа. (карточки)

          Назовите числа в порядке возрастания.

          Сосчитайте устно примеры и закрасьте фигуру.

          Кто получился? Проверьте.

          Сколько квадратов? Треугольников? Кругов? Прямоугольников?

          Какая фигура лишняя? Почему? (Нет углов.)

Практическая работа

1.                Составьте треугольник.

          Почему так называется? Сколько сторон? Сколько вершин? Сколько углов? Сколько потребовалось палочек?

2. Составьте четырехугольник.

          Почему так называется? Сколько сторон? Сколько вершин? Сколько углов? Сколько потребовалось палочек?

          А если мы возьмем 5 палочек. Какую фигуру можно составить?

          Почему так называется? Сколько сторон? Сколько вершин? Сколько углов? Сколько потребовалось палочек?

          А если мы возьмем 6 палочек. Какую фигуру можно составить?

          Почему так называется? Сколько сторон? Сколько вершин? Сколько углов? Сколько потребовалось палочек?

Вывод: Сколько углов, вершин и сторон у этих фигур? Как можно назвать эти фигуры?

А знаете, как получить восьмиугольник из квадрата?

— Я расскажу вам сейчас историю, которая произошла с нашими гостями Треугольником и Квадратом.

Жили-были два брата: Треугольник с Квадратом. Старший — квадратный, Добродушный, приятный. Младший — треугольный, Вечно недовольный. Стал расспрашивать Квадрат: “Почему ты злишься, брат?”

Тот кричит ему: “Смотри, Ты полней меня и шире, У меня углов лишь три, У тебя же их четыре!” Но Квадрат ответил: “Брат! Я же старший, я — Квадрат!” И сказал еще нежней: Неизвестно, кто нужней!”

Но настала ночь, и к брату, Натыкаясь на столы, Младший лезет воровато Срезать старшему углы. Уходя сказал: “Приятных Я тебе желаю снов! Спать ложился, был квадратным, А проснешься без углов!”

 

в) Практическая работа.

— Что сделал младший брат? (Срезал углы.)

— У вас на столе лежат квадраты. Загните у них углы. Какая фигура получилась?

— Посчитайте, сколько углов получилось? (Восемь.)

Но на утро младший брат Страшной мести был не рад. Поглядел он, нет Квадрата.

Онемел, стоял без слов… Вот так месть! Теперь у брата Восемь новеньких углов.

 

— Какое еще название можно дать этой фигуре? (Восьмиугольник.)

— От чего же зависит название многоугольника?

Вывод: название многоугольника зависит от количества углов.

— Сколько сторон было у квадрата?

— Сколько углов?

— Сколько стало сторон?

— Сколько стало углов?

Вывод: название многоугольников зависит и от количества сторон.

— Одинаково ли количество углов и сторон у каждого многоугольника? (Да.)

3. Закрепление.

а) — Резиночка желает проверить, как вы умеете распознавать многоугольники.

Дети работают цветными сигналами.

— Покажите четырехугольники; треугольники; восьмиугольники.

— Как можно назватьфигуры, которые вы показали? (Многоугольники.)

— Все ли здесь многоугольники? Покажите “лишнюю” фигуру. Почему?

б) Физминутка под музыку.

Дети стоят, звучит музыка.

— Ребята, давайте представим, что мы с вами очутились на лесной полянке. Закройте глаза, и представьте, что светит яркое солнышко, щебечут птички. Вот из под куста выглядывает треугольник, а там за елью спрятался квадрат. За деревьями притаились и другие геометрические фигуры. Им очень хочется с вами встретиться и подружиться. Откройте глаза. Покажите и назовите фигуры. Докажите.

На доске геометрические фигуры.

— Как называются все эти фигуры? (Многоугольники.)

— А если я возьму два отрезка, получится ли многоугольник? (Нет.)

— Какое минимальное количество сторон и углов может быть у многоугольников? (Три.)

в). Итоговая самостоятельная работа-тест.

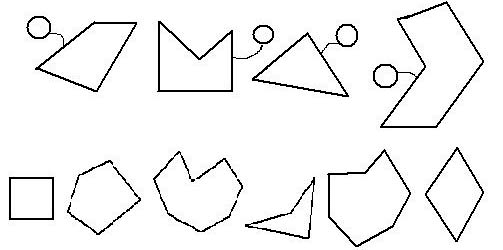
Инструктаж. На самостоятельную работу отводится 3 минуты.

1.                Сосчитай число сторон и углов многоугольников и назови их.
2.                Обведи красным цветом 5-угольники, синим — 4-угольники, зеленым — 7-угольники.
3.                Как называется оставшийся многоугольник?

г). Дополнительное задание.

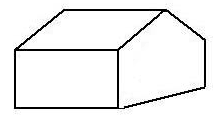
— Ученый Ластик предлагает посчитать количество многоугольников на чертеже.

д) Зрительная проверка.

4. Графический диктант.

а) — Пишем: 8 кл. вверх, 4 кл. вправо вниз по диагонали, 4 кл. влево вниз по диагонали, 5 кл. вправо, 8 кл. вверх, 4 кл. вправо вниз по диагонали, 4 кл. влево вниз по диагонали, 6 кл. вправо, 3 кл. влево вниз по диагонали, 8 кл. влево, 3 кл. влево вверх по диагонали, 3 кл. вправо.

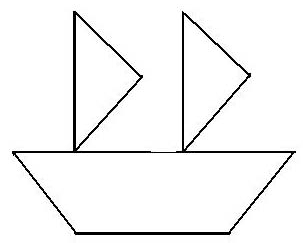
б) Зрительная самопроверка.

— Какую фигуру напоминает корпус лодки?

5. Головоломка “Танграм”.

— Возьмите игру “Танграм” и сложите эту лодочку. (1 ученик работает на фланелеграфе.)

6. Итог урока.

— С какими фигурами познакомились?

— От чего зависит название многоугольников?

— Какое количество углов и сторон должно быть у каждого многоугольника?

— Какое минимальное количество сторон у многоугольников?

7. Работа в группах. Кроссворд.

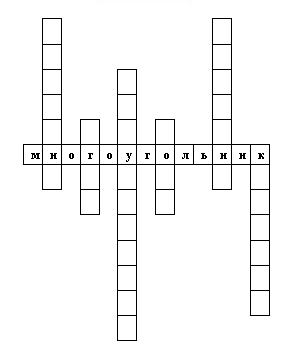
а) — Точка, из которой исходят лучи.

— Уголь, без “ь”.

— Фигура, у которой 3 угла, 3 стороны, 3 вершины.

— Фигура, у которой 4 стороны и противоположные углы равны.

— Как называются лучи, образующие угол?

— Фигура, у которой все стороны равны.

б) Зрительная проверка.

— Ученый Ластик и Резиночка благодарят вас за урок. Молодцы. Урок окончен.

5. Итог урока. Рефлексия.