Целью исследования была разработка математической модели определения оптимального уровня логистического сервиса предприятия. В результате исследования, разработана модель динамического программирования, максимизирующая прибыль предприятия при соблюдении ряда ограничений. Предложен алгоритм поиска решения с помощью рекуррентного соотношения, соответствующего основному функциональному уравнению Беллмана. Особенностью разработанной модели является возможность последовательного рассмотрения влияния значений различных показателей логистического сервиса на прибыль предприятия.
Ключевые слова: оптимизация сервиса, логистический сервис, модель динамического программирования, уровень логистического сервиса, уровень обслуживания, рекуррентные соотношения, основное функциональное уравнение Беллмана
Особенности взаимодействия подразделений маркетинга и логистики часто рассматриваются в специализированной литературе по логистическому менеджменту [1, 4, 8, 11]. Целью взаимодействия указанных подразделений предприятия является определение оптимального уровня обслуживания клиентов, который часто называют балансом «затраты/сервис» [9, 10]. Требования к логистическому сервису устанавливаются маркетингом, а реализуются логистической системой предприятия. При этом методы определения оптимального уровня логистического сервиса разработаны недостаточно. Существуют различные подходы к решению данной проблемы, один из которых основан на математическом моделировании [6]. Целью исследования была разработка математической модели определения оптимальных значений показателей логистического сервиса. Для поиска оптимального решения применен метод динамического программирования, позволяющий последовательно оценить влияние значений показателей логистического сервиса на прибыль предприятия.
Постановка задачи
Предприятие реализует продукт, под которым понимается совокупность товара и логистического сервиса. Логистический сервис характеризуется несколькими компонентами (показателями) логистического сервиса. Компоненты логистического сервиса могут быть реализованы в нескольких вариантах исполнения каждый. Варианты исполнения — это числовые значения компонентов логистического сервиса. Каждому компоненту логистического сервиса соответствует единственный вариант исполнения.
Примером компонента логистического сервиса предприятия может быть длительность функционального цикла. Длительность функционального цикла может быть различной, например 7 дней. В таком случае, 7 дней — это вариант исполнения компонента логистического сервиса. Возможные варианты исполнения компонента сервиса могут быть разные, но реализован компонент логистического сервиса может быть только в одном варианте исполнения. Длительность функционального цикла не может быть одновременно равна 5 и 7 дням.
Изменение принятого варианта исполнения компонента логистического сервиса предприятия влечет изменение значений выручки и общих операционных затрат [5] (далее общих затрат). Известны коэффициенты, отражающие изменение значений выручки и общих затрат относительно базовых значений выручки и общих затрат. Базовые значения — это значения показателей выручки и общих затрат, вызванные реализацией базового уровня логистического сервиса. Базовый уровень сервиса — это минимальный уровень сервиса, обслуживание на котором может быть предоставлено всем без исключения клиентам [1]. Вариантам исполнения, соответствующим базовому уровню логистического сервиса, заданы коэффициенты равные единице.
Предположим базовые значения выручки и общих затрат равны 60 млн. руб. и 40 млн. руб. соответственно. Изменение принятого варианта исполнения длительности функционального цикла с 7 дн. на 5 дн. влечет изменение значений выручки и общих затрат. Изменения этих значений отражены известными коэффициентами 1,25 и 1,2 для значений выручки и общих затрат соответственно. Следовательно, при длительности функционального цикла предприятия равной 5 дням выручка предприятия составит 75 млн. руб., общие затраты — 48 млн. руб.
Требуется определить такую комбинацию вариантов исполнения компонентов логистического сервиса, при которой прибыль предприятия будет максимальна. Прибыль понимается как разница между выручкой и общими затратами. При этом затраты предприятия ограничены максимальным значением.
Разработка математической модели
Для решения задачи методом динамического программирования следует рассчитать прирост общих затрат и прибыли для каждого варианта исполнения каждого компонента сервиса.
Значения прироста затрат и выручки определяются по формулам:
![]() (1)
(1)
где i — номер компонента логистического сервиса,
n — количество компонентов логистического сервиса,
j — номер варианта исполнения компонента логистического сервиса,
m — количество вариантов исполнения компонентов логистического сервиса,
![]() — прирост затрат от j-ого варианта исполнения i-ого компонента сервиса,
— прирост затрат от j-ого варианта исполнения i-ого компонента сервиса,
TCb — общие логистические затраты при реализации базового уровня сервиса,
![]() — коэффициент, учитывающий влияние j-ого варианта исполнения i-ого компонента сервиса на общие затраты.
— коэффициент, учитывающий влияние j-ого варианта исполнения i-ого компонента сервиса на общие затраты.
![]() (2)
(2)
где ![]() — прирост выручки от j-ого варианта исполнения i-ого компонента сервиса,
— прирост выручки от j-ого варианта исполнения i-ого компонента сервиса,
Rb — выручка при реализации базового уровня сервиса,
![]() — коэффициент, учитывающий влияние j-ого варианта исполнения i-ого компонента сервиса на выручку.
— коэффициент, учитывающий влияние j-ого варианта исполнения i-ого компонента сервиса на выручку.
Максимальное приращение общих затрат определяется по формуле:
![]() (3)
(3)
где ![]() — максимальное приращение общих затрат,
— максимальное приращение общих затрат,
![]() — максимальное значение общих затрат предприятия.
— максимальное значение общих затрат предприятия.
Прирост прибыли определяется по формуле:
![]() (4)
(4)
где ![]() — прирост прибыли от j-ого варианта исполнения i-ого компонента сервиса.
— прирост прибыли от j-ого варианта исполнения i-ого компонента сервиса.
Очевидно, что прирост прибыли ![]() является функцией от прироста общих затрат
является функцией от прироста общих затрат ![]() , которые ограничены, т. е.
, которые ограничены, т. е. ![]() . Таким образом, задача сводится к распределению прироста общих затрат таким образом, чтобы максимизировать прирост прибыли от всех компонентов логистического сервиса.
. Таким образом, задача сводится к распределению прироста общих затрат таким образом, чтобы максимизировать прирост прибыли от всех компонентов логистического сервиса.
Прирост общих затрат от i-ого компонента сервиса рассчитывается по формуле:
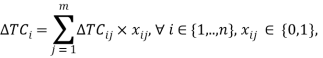 (5)
(5)
где ![]() — прирост общих затрат от i-ого компонента сервиса,
— прирост общих затрат от i-ого компонента сервиса,
![]() — булева переменная, означающая принятие или отказ от j-ого варианта исполнения i-ого компонента логистического сервиса.
— булева переменная, означающая принятие или отказ от j-ого варианта исполнения i-ого компонента логистического сервиса.
Прирост прибыли от i-ого компонента сервиса рассчитывается по формуле:
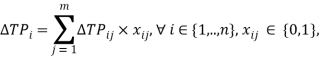 (6)
(6)
где ![]() — прирост прибыли от i-ого компонента сервиса.
— прирост прибыли от i-ого компонента сервиса.
Ранее было установлено, что прирост прибыли является функцией от прироста общих затрат, тогда:
![]() (7)
(7)
где ![]() — функция прироста прибыли, обеспеченного i-ым компонентом сервиса, от прироста затрат.
— функция прироста прибыли, обеспеченного i-ым компонентом сервиса, от прироста затрат.
Математическая модель оптимизации выглядит следующим образом:
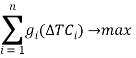 (8)
(8)
или в развернутом виде:
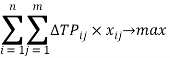 (9)
(9)
Ограничения:
![]() — булева переменная,
— булева переменная,
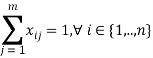 — ограничение выбора только одного варианта исполнения компонента сервиса,
— ограничение выбора только одного варианта исполнения компонента сервиса,
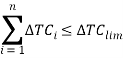 — ограничение прироста общих затрат
— ограничение прироста общих затрат
или 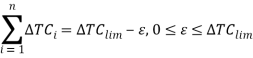 , где
, где ![]() — переменная, учитывающая разницу между фактическим приростом общих затрат и предельным.
— переменная, учитывающая разницу между фактическим приростом общих затрат и предельным.
Для решения подобных задач используются рекуррентные соотношения, соответствующие основному функциональному уравнению Беллмана [2]. В данном случае, задача может быть решена путем последовательного решения рекуррентных уравнений, основанных на следующем рекуррентном соотношении:
![]()
![]() (10)
(10)
где s — стадия поиска решения,
![]() — функция прироста прибыли на s-ой стадии решения задачи,
— функция прироста прибыли на s-ой стадии решения задачи,
![]() — функция прироста прибыли на стадии решения задачи, предшествующей s.
— функция прироста прибыли на стадии решения задачи, предшествующей s.
Предполагается, что поиск оптимального решения задачи разделен на s этапов (стадий). Поиск решения начинается с рассмотрения только одного компонента логистического сервиса, т. е. рассмотрения значений прироста прибыли от прироста затрат на реализацию компонента логистического сервиса во всех возможных вариантах исполнения. На каждой из стадий поиска решения в рассмотрение добавляется новый компонент логистического сервиса. Процесс поиска решения продолжается до тех пор, пока не будут учтены все компоненты логистического сервиса. Переменная s введена для того чтобы подчеркнуть многоэтапность процесса поиска решения и избежать путаницы в значениях прироста прибыли вызванного реализацией компонента сервиса и прироста прибыли на какой-либо из стадий поиска решения. Последнее значение может учитывать значения прироста прибыли, вызванные реализацией нескольких компонентов логистического сервиса.
Решение числового примера схожей задачи с необходимыми пояснениями предложено в статье [7].
Анализ задачи
Необходимо отметить несколько предположений относительно исходных данных разработанной модели. Предполагается, что известны коэффициенты, отражающие влияние вариантов исполнения компонентов логистического сервиса на выручку и общие затраты предприятия. Разумеется, такие данные могут быть неизвестны или известны не полностью. Однако эти данные могут быть получены методом интерполяции, а также на основе установления регрессии [3, 12].
Также предполагается, что компоненты логистического сервиса влияют на значения выручки и общих затрат изолированно друг от друга. Это предположение выражается в линейности целевой функции модели. Таким образом, возможный синергетический эффект влияния компонентов логистического сервиса не учитывается. Выявление и формализация такого эффекта существенно усложнит модель и поиск решения.
Результаты
В результате исследования разработана модель динамического программирования, целью которой является оптимизация логистического сервиса предприятия. Для определения оптимальных значений показателей логистического сервиса предложено рекуррентное соотношение, составленное в соответствии с основным функциональным уравнением Беллмана. Отмечены некоторые предположения и допущения относительно исходных данных и целевой функции разработанной модели.
Выводы
Процесс поиска оптимального решения разделен на несколько этапов, что обеспечивает ряд преимуществ для лица принимающего решения (ЛПР). В частности, решая задачу поэтапно, ЛПР имеет возможность последовательно рассмотреть влияние значения каждого показателя логистического сервиса на значения финансовых показателей предприятия. Кроме того, ЛПР имеет возможность принять к реализации «удовлетворительное» решение, а не математически оптимальное. Таким образом, модель динамического программирования оставляет место интуиции и опыту ЛПР при принятии решения относительно логистического сервиса предприятия, что повышает вероятность практической реализации разработанной модели.
Литература:
- Бауэрсокс Д.Дж., Клосс Д.Дж. Логистика: интегрированная цепь поставок / Д.Дж. Бауэрсокс, Д.Дж. Клосс, перевод Н. Н. Барышникова, Б. С. Пинскер. — 2-е изд. — М.: ЗАО «Олимп-Бизнес», 2008. — 640 c.
- Беллман Р. Динамическое программирование / Р. Беллман, под ред. Н. Н. Воробьева. — М.: Издательство иностранной литературы, 1960. — 400 c.
- Вохмянина А. В. Математическая модель экономического обоснования уровня сервиса логистических центров // Вестник Уральского государственного университета путей сообщения. — 2009. — № 3–4. — C. 109–117.
- Дыбская В. В. [и др.]. Логистика / В. В. Дыбская, Е. И. Зайцев, В. И. Сергеев, А. Н. Стерлигова, под ред. В. И. Сергеева. — М.: Эксмо, 2014. — 944 c.
- Ильин И. В. Оценка трансакционных издержек при формировании экономической стратегии фирмы // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. — 2003. — № 4 (34). — C. 88–97.
- Ильин И. В., Рыбаков Д. С. Обзор подходов к определению и решению проблемы взаимодействия маркетинга и логистики торгового предприятия // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Экономические науки. — 2015. — № 6 (233). — C. 123–137.
- Рыбаков Д. С. Модель оптимизации логистического сервиса торгового предприятия // Логистика и управление цепями поставок. — 2015. — № 6 (71). — C. 63–76.
- Сергеев В. И. Корпоративная логистика. 300 ответов на вопросы профессионалов. — М.: ИНФРА-М, 2005. — 976 c.
- Сергеев В. И. Проблема определения баланса «затраты/уровень обслуживания» для целей стратегического планирования логистики // Логистика и управление цепями поставок. — 2011. — № 5 (46). — C. 5–14.
- Сергеев В. И., Бурмистрова Н. С. Управление качеством логистического сервиса сетевого ритейлера путем оптимизации баланса «затраты/сервис» // Логистика и управление цепями поставок. — 2011. — № 4 (45). — C. 14–26.
- Christopher, M. (2011), Logistics and Supply Chain Management, 4th ed., Financial Times/Prentice Hall, Dorchester, Dorset.
- Jeffery, M.M., Butler, R.J. and Malone, L.C. (2008), “Determining a cost-effective customer service level”, Supply Chain Management: An International Journal, Vol. 13 No. 3, pp. 225–232.

