Анализ издержек обращения торговых организаций с применением статистического метода структурных средних
Автор: Чернова Алла Геннадиевна
Рубрика: 10. Учет, анализ и аудит
Опубликовано в
Дата публикации: 10.12.2014
Статья просмотрена: 200 раз
Библиографическое описание:
Чернова, А. Г. Анализ издержек обращения торговых организаций с применением статистического метода структурных средних / А. Г. Чернова. — Текст : непосредственный // Проблемы и перспективы экономики и управления : материалы III Междунар. науч. конф. (г. Санкт-Петербург, декабрь 2014 г.). — Санкт-Петербург : Заневская площадь, 2014. — С. 165-167. — URL: https://moluch.ru/conf/econ/archive/131/6859/ (дата обращения: 23.04.2024).
Большое значение в рамках анализа издержек обращения торгового предприятия отводится изучению издержкоемкости.
Показатель издержкоёмкости — это отношение издержек обращения к товарообороту и определяется по формуле: ИЁ = ИО*100/ ТО, где ИЁ – издержкоёмкость; ИО — сумма издержек обращения; ТО — товарооборот.
Уровень издержек обращения (издержкоемкость реализации товаров) — это сумма затрат, приходящаяся на 100 руб. розничного товарооборота. На издержкоемкость оказывает влияние общая сумма издержек, которая находится в прямой зависимости от изменения объема товарооборота, структуры товарооборота, цены на реализуемые товары, издержек обращения по видам ресурсов и т. п. [1с.73]
Для анализа издержкоёмкости ряда предприятий можно использовать один из видов средних величин — структурные средние, который применяется для изучения внутреннего строения рядов распределения значений признака. [2 с.56]
Из структурных средних в основном используют показатели: моды — наиболее часто повторяющегося значения признака, а также медианы — величины признака, которая делит упорядоченную последовательность его значений на две равные части по численности. В частности у одной половины единиц совокупности значение признака не превышает медианного уровня.
В статистике модой является величина признака (варианта), которая наиболее часто встречается в данной совокупности. В вариационной последовательности это будет варианта, имеющая наибольшую частоту. Показатель «мода» применяется в тех случаях, когда нужно охарактеризовать наиболее часто появляющуюся величину признака.
Медианной называется варианта, располагающаяся в середине вариационного ряда. Этот показатель делит анализируемый ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности.
Медиана показывает количественную границу, величину варьирующего признака, которую достигла половина членов совокупности.
Исходным моментом предлагаемой методики анализа издержек обращения является возможность формирования информации о величинах торговых затрат группы предприятий, а также данных об средних размерах издержкоёмкости. Эти данные могут использоваться для аналитических выводов и планирования.
Для анализа издержкоёмкости торговых предприятий были взяты данные 34 организаций.
Выполним статистическую группировку показателей 34 магазинов. Определим число групп по формуле Стерджесса: N = 1+3.322 lg N = 1+ 3.322 lg 34 = 5,
где N- численность совокупности торговых предприятий (34 организации).
Затем следует определение величины интервала по формуле:
h = (Xmax — Xmin)/5 = (1254–529)/ 5 = 725 / 5 = 145 руб.,
где Xmax и Xmin соответственно максимальное и минимальное значения издержкоёмкости предприятий.
Таблица 1
Расчёт данных для показателей медианы и моды
|
Группы по издержко- ёмкости, руб. |
Число торговых предприятий, m |
Центр интервала, Х |
Хm |
Накопленная частота, S |
Хср =Хm/m |
Х -Хср |
|
529–674 |
18 |
602,5 |
10845,0 |
18+0 =18 |
|
-136 |
|
674–819 |
7 |
746,5 |
5225,5 |
18+7 = 25 |
|
8 |
|
819–964 |
4 |
891,5 |
3566,0 |
25+4 = 29 |
|
153 |
|
964–1109 |
3 |
1036,5 |
3109,5 |
29+3 = 32 |
|
298 |
|
1109- 1254 |
2 |
1181,5 |
2363,0 |
32+2 = 34 |
|
443 |
|
Итого |
34 |
- |
25108,5 |
- |
738,5 |
- |
С помощью интерполяции в медианном интервале находим значение медианы:
Ме = Хmin + h* ((∑m/2 — Sм) / m),
где Xmin–нижняя граница медианного интервала;
h–величина медианного интервала;
∑ m/2 — половина от общего числа наблюдений;
SM-1 — сумма наблюдений, накопленная до начала медианного интервала;
m — число наблюдений.
Используя данные таблицы 1, вычислим величину медианы:
Ме = 529 + 145*((34/2–0) / 18) = 665,94 руб.
Этот показатель свидетельствует о том, что у половины предприятий издержкоёмкость превышает 665,94 руб., половина всего товарооборота производится с учётом 666 руб. на единицу издержек, и 50 % общей суммы издержек обращения образуется при определённом показателе. Заметим также, что наблюдается положительная тенденция к снижению издержкоёмкости, так как Ме = 665,94 руб., а средний уровень равен 738,5 руб. Для интервального ряда с равными интервалами мода определяется по формуле:
Мо = Хmin + h* (mMo — mMo-1 / (mMo — mMo-1) + (mMo + mMo+1)),
где Хmin — нижнее значение модального интервала; h — величина модального интервала;
mMo — число наблюдений;
mMo-1 — число наблюдений для интервала, предшествующего модальному;
mMo+1 — число наблюдений для интервала, следующего за модальным.
По данным таблицы 1, вычислим величину моды:
Мо = 529 + 145* ((18–0)/ 18+(18–7) = 529 + 145*(18/29) = 619 руб.
Смысл этой формулы состоит в следующем: величину той части модального интервала, которую нужно прибавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. В данном случае к минимальному значению данных 529 прибавляем 90, т. е. больше половины интервала (145/2), потому что частота предшествующего интервала меньше частоты последующего интервала. Таким образом, чаще всего встречаются предприятия с издержкоёмкостью 619 руб.
Соотношение моды, медианы и средней арифметической указывает на характер распределения и его асимметрию. Выполним сравнение показателей:
Хср > Ме > Мо = 738,5руб. > 665,94руб. > 619,00руб.
738,5–665,94 = 72,56 руб. и 665,94–619,00 = 46,94 руб.
Представленное распределение имеет правостороннюю асимметрию.
Таблица 2
Расчёт данных для показателей отклонений
|
Группы, руб. |
Число, m |
Хср = Хm/m |
Х -Хср |
(Х –Хср) 2 |
(Х –Хср)2 *m |
|
529–674 |
18 |
|
-136 |
-136 2 = 18496 |
18496*18 = 332928 |
|
674–819 |
7 |
|
8 |
82 = 64 |
64*7 = 448 |
|
819–964 |
4 |
|
153 |
1532 = 23409 |
23409 * 4 = 93636 |
|
964–1109 |
3 |
|
298 |
2982 = 88804 |
88804 * 3 = 266412 |
|
1109–1254 |
2 |
|
443 |
4432 = 196249 |
196249 * 2 = 392498 |
|
Итого |
34 |
738,5 |
- |
|
1085922 |
Квадратическое отклонение: δ = 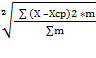 =
= 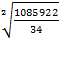 = 178,7руб.
= 178,7руб.
На эту величину откланяются показатели издержкоёмкости анализируемых предприятий.
V = δ*100/ Хср = 178.7* 100/ 738,5 = 24,2 %.
Так как 33 % >24 %, то совокупность показателей однородная.
Асимметрия: А = (Хср — Мо)/ δ = (738,5–619) /178,7 = 0,668.
Определённый показатель значительный и правосторонний.
На основе проведённого анализа можно оценить эффективность использования издержек обращения по сравнению с другими организациями и выполнить планирование.
Литература:
1. Экономика и организация деятельности торговых предприятий. Учебное пособие/Под общ. ред. А. Н. Соломатина. — М.: ИНФРА-М, 2000.- 295 с.
2. Чернова Т. В. Экономическая статистика. Учебное пособие. Таганрог: Изд-во ТРТУ, 1999.- 356 с.
Похожие статьи
Исследование моды и медианы результатов ЕГЭ по математике
- величина медианного интервала.
частота медианного интервала. Медиана может быть определена графически по кумуляте.
Модальным является интервал «от 40 до 50», т. к. он имеет наибольшую частоту.
Вариационный ряд антропометрических признаков студенток...
В том случае, если в выборке число наблюдений менее 60, значения признака не группируют в классы. Интервал между двумя соседними классами — классовый интервал — определяют по формуле [1].
Применение методов скользящей средней, экспоненциального...
m — нечетное число уровней, входящих в интервал сглаживания. yi — фактический уровень. При этом значения yi, которые относятся к будущим периодам, определяют по формуле
где: n — число наблюдений, входящих в интервал сглаживания.
Анализ дифференциации населения по уровню доходов...
i — величина интервала
fМо+1 — частота интервала, следующего за модальным. медианный доход- показатель дохода, находящегося в середине ранжированного ряда распределения: [2, c. 445].
Статистические методы при управление качеством продукции на...
Число интервалов k находим по формуле
Число интервалов k примем равным 4. Тогда ширина интервала.
Организация внедрения статистических методов управления качеством продукции на предприятии.
Мода и медиана вариационного ряда антропометрических...
— частота интервала, следующего за модальным. Определить модальное значение признака можно и по графику. Если число единиц будет четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
Решение задач анализа и синтеза на имитационных моделях...
При большом числе наблюдений значения случайной величины группируют по интервалам (разрядам) и представляют графически в виде гистограммы. Количество интервалов определяется по формуле Стерджеса Г. А.
Вычисление статистических показателей с использованием...
- показатели центра распределения (средняя величина, мода, медиана)
Кроме указанных значений рассчитываются доверительные интервалы для математического ожидания и среднего квадратического
Статические обработки результатов наблюдений при проведении...
Экономический анализ влияния стабильности оборотных активов...
С помощью данных показателей дается оценка динамики изменения структуры [2, с.21].
Расчет индекса А. Салаи, тем не менее, имеет особенность, которую можно отнести к недостаткам, – его величина значительно меняется с изменением элементов, на которые...
Похожие статьи
Исследование моды и медианы результатов ЕГЭ по математике
- величина медианного интервала.
частота медианного интервала. Медиана может быть определена графически по кумуляте.
Модальным является интервал «от 40 до 50», т. к. он имеет наибольшую частоту.
Вариационный ряд антропометрических признаков студенток...
В том случае, если в выборке число наблюдений менее 60, значения признака не группируют в классы. Интервал между двумя соседними классами — классовый интервал — определяют по формуле [1].
Применение методов скользящей средней, экспоненциального...
m — нечетное число уровней, входящих в интервал сглаживания. yi — фактический уровень. При этом значения yi, которые относятся к будущим периодам, определяют по формуле
где: n — число наблюдений, входящих в интервал сглаживания.
Анализ дифференциации населения по уровню доходов...
i — величина интервала
fМо+1 — частота интервала, следующего за модальным. медианный доход- показатель дохода, находящегося в середине ранжированного ряда распределения: [2, c. 445].
Статистические методы при управление качеством продукции на...
Число интервалов k находим по формуле
Число интервалов k примем равным 4. Тогда ширина интервала.
Организация внедрения статистических методов управления качеством продукции на предприятии.
Мода и медиана вариационного ряда антропометрических...
— частота интервала, следующего за модальным. Определить модальное значение признака можно и по графику. Если число единиц будет четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
Решение задач анализа и синтеза на имитационных моделях...
При большом числе наблюдений значения случайной величины группируют по интервалам (разрядам) и представляют графически в виде гистограммы. Количество интервалов определяется по формуле Стерджеса Г. А.
Вычисление статистических показателей с использованием...
- показатели центра распределения (средняя величина, мода, медиана)
Кроме указанных значений рассчитываются доверительные интервалы для математического ожидания и среднего квадратического
Статические обработки результатов наблюдений при проведении...
Экономический анализ влияния стабильности оборотных активов...
С помощью данных показателей дается оценка динамики изменения структуры [2, с.21].
Расчет индекса А. Салаи, тем не менее, имеет особенность, которую можно отнести к недостаткам, – его величина значительно меняется с изменением элементов, на которые...











