Одной из причин наблюдаемой в эксперименте зависимости концентрационной константы устойчивости комплексного соединения от состава смешанного водно-органического растворителя является необоснованное применение закона действия масс к упрощенно отображенному равновесию комплексообразования. В некоторых случаях можно найти аналитическое описание данной зависимости, не прибегая к методу активностей.
Ключевые слова: моделирование равновесий комплексообразования, константа устойчивости, влияние органического растворителя на прочность комплекса, сольватация, донорно-акцепторный механизм
В публикациях по физической и аналитической химии уделяется большое внимание вопросу влияния состава водно-органической среды на устойчивость комплексных соединений [1]. Ранее исследования в данной области касались решения практических задач, например, поиска лучших условий хроматографического разделения радионуклидов РЗЭ [2]. В фундаментальном аспекте вопрос по-прежнему актуален, т. к. имеет отношение к теории растворов, и его решение позволило бы углубить представления о механизмах сольватации.
Цель данной работы показать, что одной из причин экспериментально наблюдаемого изменения концентрационной (инструментальной) константы устойчивости комплексного соединения в зависимости от состава водно-органического растворителя, является некорректная формулировка равновесий комплексообразования, выполненная без учета взаимодействия компонентов реакции с молекулами среды. В ряде случаев эта зависимость может быть описана аналитически как функция состава раствора. Рассмотрение вопроса касается равновесий в замкнутой системе при постоянных — температуре, давлении, объеме и концентрации солевого фона.
В соответствии с классическим определением, концентрационная суммарная ступенчатая константа устойчивости βk комплекса MAk в растворе
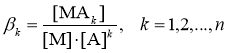
![]() (1)
(1)
рассматривается как константа равновесия
M + kA ↔ MAk.(2)
Здесь и далее заряды не указываются, концентрации молярные.
Согласно современным представлениям [1], молекулы воды и органических донорных растворителей принимают непосредственное участие в равновесиях образования-диссоциации комплексных соединений в растворах, выступая в качестве конкурента по отношению к лиганду в сольватации частиц, прежде всего — центрального катиона комплекса. Этот процесс, обозначаемый также термином «лигандный обмен», имеет в своей основе донорно-акцепторный механизм. Однако вышеуказанное определение данного обстоятельства не учитывает. Сформулированное в таком виде, оно относится скорее не к жидкой среде, а к воображаемому равновесию в вакууме [1, стр. 46]. Поэтому в случае растворов величина βk превращается из константы в сложный функционал состава среды и целого ряда параметров неучтенных взаимодействий компонентов реакции (2) со средою растворителя. Фиксация данного функционала в растворителе постоянного состава (например, в воде) обеспечивается постоянством концентрации растворителя и, как принято считать, присутствием фонового электролита. Но переход от среды одного растворителя к смешанным средам почти всегда оказывает очень сильное влияние на величину βk, поскольку меняется молекулярно-стехиометрический состав среды растворителя — важнейшая характеристика системы.
Известно, что методы измерения констант комплексообразования в водно-органических средах базируются на тех же принципах, что были изначально разработаны для водных растворов. Тем же остается в своей основе и аппарат обработки опытных данных при оценке компонентов вектора ![]() искомых параметров, где упрощенное определение (1) и сопряженный с ним баланс (2) используются как базис для построения соответствующей математической модели. В результате наблюдается неизбежное явление: замена части воды на органический растворитель приводит к тому, что значения найденных концентрационных констант
искомых параметров, где упрощенное определение (1) и сопряженный с ним баланс (2) используются как базис для построения соответствующей математической модели. В результате наблюдается неизбежное явление: замена части воды на органический растворитель приводит к тому, что значения найденных концентрационных констант ![]() , так или иначе, изменяются с изменением состава смешанного растворителя. Накопленный фактический материал, касающийся данного феномена, огромен.
, так или иначе, изменяются с изменением состава смешанного растворителя. Накопленный фактический материал, касающийся данного феномена, огромен.
С позиций метода активностей рассматриваемое явление трактуется как «отклонение системы от идеальности», и непостоянство концентрационной константы устойчивости приписывается изменению коэффициентов активности частиц, участвующих в реакции (2) [4, 5]. Такая трактовка вполне соответствует принципу, по которому «закон действия масс выполняется лишь для активностей химических форм» [3]. Принцип стал каноническим, вошел во все учебники по физической химии растворов и многими исследователями стал восприниматься не как эмпирический факт, а как следствие некой доказанной теоремы. В модельных представлениях, основанных на методе активностей, большая роль отводится эффектам влияния среды растворителя, особенно диэлектрической проницаемости (ε), на электростатические взаимодействия заряженных частиц в растворе. Данный фактор до сих пор считается наиболее существенным для комплексных соединений «ионного» типа в среде растворителей, «близких по химической природе» [1, стр. 74]. Соответствующая данным представлениям модель («электрохимическая модель сольватации»), как известно, предсказывает линейную взаимосвязь lgβk от величины ε-1 среды растворителя. Модель ранее широко обсуждалась в литературе, однако себя не оправдала по самой простой причине: она не учитывает, что в водно-органических средах один, по меньшей мере, компонент системы — вода — является активным донором электронных пар для центрального катиона комплекса, а в большинстве случаев — и оба компонента. Следовательно, в ряду водно-органических сред вряд ли вообще имеются системы, в которых сольватация по донорно-акцепторному механизму менее существенна, чем сольватация по электростатическому механизму, поскольку энергия первой существенно выше последней [6].
Если же подойти к вопросу о влиянии среды на равновесия комплексообразования с позиций донорно-акцепторной модели сольватации, то необходимо будет признать:
– уравнение реакции (2) в случае растворов, в том числе и водных, отражает не реальное равновесие, а всего лишь суммарный («брутто») баланс металл–лиганд;
– соответственно не имеет под собой реальной физико-химической основы выражение (1) для константы равновесия.
Указанных обстоятельств уже более чем достаточно для того, чтобы концентрационная константа устойчивости (которую лучше назвать опытной или инструментальной псевдоконстантой), определяемая в соответствии с формулой (1), обнаружила зависимость от состава водно-органической среды. Но связывать данное явление следовало бы, прежде всего, не с изменением каких-либо электрофизических параметров среды, а с принципиальной методологической ошибкой — приложением закона действия масс к неверно отображенному равновесию. На языке математического моделирования подобный случай обозначается термином «использование бессодержательной модели». Как это происходит, и что из этого следует, будет показано на простейшем примере.
Пусть в водном растворе имеет место равновесие лигандного обмена:
MWh + k A ↔ MWh-kdAk + kdW,(3)
(h — координационное число, d — дентатность лиганда, W — молекула воды); соответствует случаю, когда донорно-акцептороное взаимодействие между M и W сильное, а между A и W — существенно слабее. Концентрационная константа равновесия этой реакции
![]() (4)
(4)
В воде величина [W] постоянна, поэтому член [W]kd формулы (4) можно включить в константу Kk, а символ «W« опустить. Именно такое «преобразование» лежит в основе упрощенных соотношений (1, 2), причем в выражении (1)
![]() .(5)
.(5)
Теперь мысленно представим себе, что в раствор добавляется органический растворитель, молекулы которого обладают значительно более слабой электронодонорной функцией по сравнению с молекулами воды в отношении катиона металла-комплексообразователя. Новых частиц, участвующих в комплексообразовании не появится, поэтому уравнений (3) и (4) достаточно для описания равновесий в растворе. Однако по мере увеличения содержания органического компонента в смешанном растворителе будет снижаться концентрация воды, и объединение члена [W]kd с величиной Kk неправомерно. Если данного обстоятельства не учитывать (как не учитывает его, в частности, электростатическая модель сольватации), то инструментальная псевдоконстанта βk будет зависеть от концентрации воды в соответствии с формулой (5), а от объемной доли органического растворителя, ns, в соответствии со следующей формулой:
![]() ,(6)
,(6)
где [W]0 — концентрация воды в среде без органического растворителя, ![]() - значение βk в воде. Очевидно, было бы нелогичным объяснять такую зависимость изменением каких-либо параметров среды, помимо [W], например, диэлектрической проницаемости, пытаться учесть действие этих факторов путем введения активностей частиц вместо их стехиометрических концентраций, а потом исследовать зависимости коэффициентов активности от состава и «природы растворителя» и т. п.
- значение βk в воде. Очевидно, было бы нелогичным объяснять такую зависимость изменением каких-либо параметров среды, помимо [W], например, диэлектрической проницаемости, пытаться учесть действие этих факторов путем введения активностей частиц вместо их стехиометрических концентраций, а потом исследовать зависимости коэффициентов активности от состава и «природы растворителя» и т. п.
Описываемый случай дает следующий результат. Логарифмируем соотношение (5):
![]() .(7)
.(7)
Видно, что в системе с «пассивным» органическим компонентом зависимость опытной псевдоконстанты от концентрации воды в смешанном растворителе должна быть в логарифмическом масштабе линейной с тангенсом угла наклона по модулю кратным дентатности лиганда.
Приложение вывода к экспериментальным данным
Взаимосвязь вида (7) найдена в системе La, Ce(III) –иминодиацетат в смесях воды с 2-метоксиэтанолом (метилцеллозольвом, МТЦ) [2]. Экспериментальные данные (lg [W], lgβ1) адекватно описываются уравнением прямой
![]() ,(8)
,(8)
(рис., прямые 1, 2). C 95 %-ой доверительной вероятностью получены следующие МНК-оценки параметров модели (8):
lgK1 = 10.189 ± 0.074; d = 2.967 ± 0.046; r = 0,99999 (La);
lgK1 = 10.64 ± 0.66; d = 3.02 ± 0.41; r = 0,99954 (Ce);
r — коэффициент корреляции, число степеней свободы для каждой серии f = 2. Видно, что доверительные интервалы для оценок модуля тангенса угла наклона прямых включают в себя значение дентатности иминодиацетат-иона d = 3 [7]. Аналогичная закономерность проявляется на второй ступени комплексообразования: в результате внедрения второй молекулы лиганда в координационную сферу РЗЭ происходит вытеснение еще трех молекул воды, итого на двух стадиях высвобождается 6 молекул. Интервальные оценки модуля тангенса угла наклона прямых
![]() ,(9)
,(9)
аппроксимирующих данные (lg [W], lgβ2) (рис., прямые 3, 4) включают величину 2d = 6:
lgK2 = 20.0 ± 1.6; 2d = 6.43 ± 0.96; r = 0.99941 (La);
lgK2 = 20.3 ± 2.0; 2d = 6.1 ± 1.2; r = 0.99902 (Ce).
К сожалению, мы не располагаем достаточно точными данными об инструментальных псевдоконстантах β3 третьей ступени.
Как видно их полученного результата, по крайней мере для двух ступеней комплексообразования удается с большой точностью описать зависимость инструментальных псевдоконстант βk от состава водно-органического растворителя при помощи модели (6)-(7). Найденные значения параметров K1, K2 уже можно считать оценками истинных констант равновесия, но не в традиционном «термодинамическом» смысле, а в том, что они не зависят от концентрации органического компонента смешанной среды в исследованном диапазоне (в данном случае до ns = 0.6). На этом описание рассмотренных систем в оговоренных рамках исчерпывается. Основанное на строгой стехиометрии, оно оказывается предельно простым: не требуется понятий активности растворенных веществ и растворителей, отпадает вопрос о влиянии на «прочность комплекса» каких-либо дополнительных, apriori менее существенных параметров среды, в частности, диэлектрической проницаемости.
Трактовка полученного результата и дополнительные выводы:
– если органический компонент смешанного раствора не принимает активного участия в сольватации, его присутствие должно проявляться как фактор разбавления воды и учитываться путем включения воды в уравнения реакции образования-диссоциации комплекса;
– в ряду бинарных водно-органических смесей с одинаковым значением ns, составленных из воды и растворителей, обладающих существенно менее сильными электронодонорными свойствами по сравнению с водой, значения инструментальной псевдоконстанты устойчивости одного и того же комплекса должны быть примерно одинаковыми, т. к. в этих смесях [W] — величина постоянная;
– та же картина должна наблюдаться и в том случае, когда сравниваемые друг с другом органические растворители близки по своей электронодонорной функции и мало различаются по плотности и молекулярной массе (т. е. при одинаковой объемной доле в смеси с водой в одинаковой степени разбавляют воду и привносят в раствор одинаковое количество новых сольватирующих молекул).
В свете сделанных выводов важен следующий эмпирический факт. Замечено, что для ряда систем зависимость lgβk от ns является более общей, нежели зависимость от диэлектрической проницаемости среды. Иначе говоря, в смесях воды с разными растворителями при постоянном значении объемной доли ns (в диапазоне до ~ 0.4) устойчивость одного и того же комплекса оказывается приблизительно одинаковой [8, 9]. Подобная картина отмечалась и в случае иминодиацетатных [2] и миндалатных (2-гидрокси-2-фенилацетатных) [10] комплексов РЗЭ в смесях воды с разными растворителями; было высказано предположение, что решающим фактором в данных системах является не какое-либо электрофизическое свойство среды, а простая величина — содержание воды в смешанном растворителе. В рамках изложенных представлений явление получает ясное истолкование.
Рассмотренный в данной работе частный случай аналитического описания зависимости инструментальной псевдоконстанты устойчивости комплекса от состава водно-органического растворителя относится к системе с пассивным органическим компонентом среды, чья роль сводится к разбавлению воды и проявляется в сдвиге равновесия в сторону образования комплекса, в соответствии с законом действия масс. В дальнейшем, для развития и обобщения концепции, целесообразно рассмотрение систем с органическим растворителем, который наряду с водой участвует в непосредственной сольватации катиона и комплекса. Разработки в данном направлении будут полезны для развития общей теории растворов.

Рис. 1. Зависимость логарифма концентрационных констант устойчивости иминодиацетатных комплексов La и Ce от логарифма молярной концентрации воды в смесях с 2-метоксиэтанолом (2980K, 1 M LiCl); экспериментальные данные [2] и их линейная аппроксимация; 1 — моноиминодиацетат La, 2 — моноиминодиацетат Ce, 3 — дииминодиацетат La, 4 — дииминодиацетат Ce.
Литература:
- Березин Б. Д., Ломова Т. Н. Реакции диссоциации комплексных соединений. М.: «Наука», 2007. 278 с.
- Цибанов В. В., Богатырев И. О., Заборенко К. Б. //Корд. химия. 1976. 2. № 2. С. 234.
- Скопенко В. В., Цивадзе А. Ю., Савранский Л. И., Гарновский А. Д. Координационная химия. М.: ИКЦ «Академкнига», 2007. С. 366.
- Измайлов Н. А. Электрохимия растворов. М.: «Химия», 1966. 488 с.
- Россотти Ф., Россотти Х. Определение констант устойчивости и других констант равновесия в растворах. М.: «Мир», 1965. 522 с. [Rossotti F. J. C. and Rossotti H. The Determination of Stability Constants and Other Equilibrium Constants in Solutions. N.-Y.: McGraw-Hill Book Co., Inc., 1961. 425 p.].
- Измайлов Н. А., Кругляк Ю. А. //Докл. АН СССР.1960. 134. С. 1390.
- Дятлова Н. М., Темкина В. Я., Попов К. И. Комплексоны и комплексонаты металлов. М.: «Химия», 1988. С. 106.
- Бабко А. К., Драко О. Ф. //Журн. общей химии. 1950. 20. С. 228.
- Мигаль П. К., Плоае К. И. //Журн. неорган. химии. 1972. 17. С. 2626.
- Цибанов В. В. Автореферат дисс. … канд. хим. наук. М. МГУ им. М. В. Ломоносова, 1976. 31 с.

