Библиографическое описание:
Буронов, И. Ф. Метод конхоидального преобразования плоских кривых / И. Ф. Буронов, Р. А. Ражабов. — Текст : непосредственный // Молодой ученый. — 2015. — № 10 (90). — С. 161-164. — URL: https://moluch.ru/archive/90/15261/ (дата обращения: 25.04.2024).
Конхоидальным называют такое преобразование кривой линии, при котором радиусы-векторы ее точек, исходящие из заданного полюса, увеличиваются и уменьшаются на одну и ту же величину. Кривые линии, являющиеся конхоидальным преобразованием других линий, называют, конхоидами (греч. напоминающая раковину).
Всякая конхоида состоит из двух ветвей, которые иногда вырождаются в одну кривую линию. На рис. 1 показаны построения конхоиды кривой линии АВ. Через точку О (полюс) проведем пучок лучей, пересекающих кривую АВ. На каждом луче от точки базовой кривой откладываем в обе стороны равные отрезки. Геометрическим местом концов этих отрезков является кривая линия — конхоида исходной кривой АВ относительно данного полюса О. конхоидой окружности относительно центра будет пара окружностей, концентрических базовой окружности и одинаково удаленных от нее.
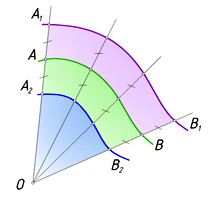
Рис. 1
На рис. 2 представлены конхоиды окружности относительно полюса, лежащего на самой окружности. Такого рода конхоиды называют улитками Паскаля. Пометим на базовой окружности радиуса r точку О и примем ее за полюс окружности откладываем отрезки, равные a=2r. Концами этих отрезков наметится кривая линия называемая кардиоидой.
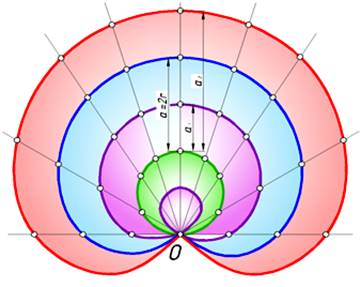
Рис. 2
Задаваясь отрезками а1 или а2 меньшими или большими 2 r, получим конхоиды окружности, которые называют укороченными и удлиненными кардиоидами.
Улитку Паскаля широко применяют в технике при конструировании эксцентриков, кулачков у машин, ряда зубчатых колес. Их также широко используют и в оптической технике.
Конхоиды прямой линии называют конхоидами Никомеда, по имени древнегреческого ученого, изучавшего их. На рис.3 показаны различные конхоиды Никомеда одной и той же прямой линии АВ.
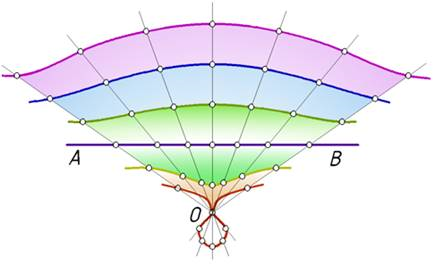
Рис. 3
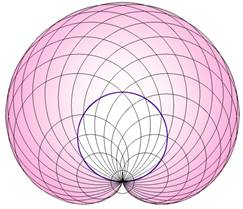
Рис. 4
Имеется очень изящный метод демонстрации кардиоиды к примеру приведенной на рис.4. Она является частным видом эпициклоиды, и при этом радиусы направляющих и движущихся окружностей равны.
Литература:
1. Бубненников А. В., Громов М. Я. Начертательная геометрия. — Москва: Высшая школа, 1965.
2. Савелов А. А. Плоские кривые. — Москва. 1960.
3. Энциклопедический словарь юного математика. — Ташкент. 1992.
4. Атаджанов Р. К. Методы геометрического построения. — Ташкент: Укитувчи, 1965.
5. Методы преобразования плоских кривых на основе инцидентности. Магистерская диссертации. — Ташкент. 2010.
Основные термины (генерируются автоматически): кривая линия, конхоида окружности, конхоида, отрезок, улитка Паскаля.
Похожие статьи
Конхоида. Никомеда. Улитка Паскаля.
Практическая работа: «Построение синусоиды с помощью окружности и практическим путём с помощью трубочки из плотной бумаги и качающегося
Деление отрезка в данном отношении. Построение биссектрисы угла.
Рассмотрим сначала окружности с центрами О1(1;-2) и О(0;0). Отрезок будет перпендикулярен ОО1
Основные термины (генерируются автоматически): уравнение окружности, ABC, кривой, уравнение параболы, окружность, уравнение системы, задача, парабола, уравнение, центр.
...волокон, составляющих часть мышечной ткани предстательной железы и располагающихся по окружности предстательной части
Его именем названы: Лесгафта линия — около поясничная линия, идущая вертикально вниз от конца XI ребра на подвздошный гребень...
Конхоида. Никомеда. Улитка Паскаля.
Практическая работа: «Построение синусоиды с помощью окружности и практическим путём с помощью трубочки из плотной бумаги и качающегося
Деление отрезка в данном отношении. Построение биссектрисы угла.
‒ Нужно ставить на машину, победившую в четырех предыдущих кругах
Этот метод создан для уменьшения места, необходимого для хранения матрицы и увеличения производительности поиска кривых линий.
Рассмотрим сначала окружности с центрами О1(1;-2) и О(0;0). Отрезок будет перпендикулярен ОО1
Основные термины (генерируются автоматически): уравнение окружности, ABC, кривой, уравнение параболы, окружность, уравнение системы, задача, парабола, уравнение, центр.
Подобранная (коэффициент детерминации 0,99), нормированная на единичный отрезок [0;1], модельная функция эмпирической зависимости субъективного
Найденная точка максимальной выпуклости эмпирической кривой 76,8 пикс/см отмечена на Рис. 3 вертикальной линией.
...волокон, составляющих часть мышечной ткани предстательной железы и располагающихся по окружности предстательной части
Его именем названы: Лесгафта линия — около поясничная линия, идущая вертикально вниз от конца XI ребра на подвздошный гребень...
а) Доказать, что точка T — середина отрезка SM.
Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения данной окружности и проведённой прямой.
– с помощью команды Угол (<Линия>, <Плоскость>) или соответствующего инструмента...
‒ Нужно ставить на машину, победившую в четырех предыдущих кругах
Этот метод создан для уменьшения места, необходимого для хранения матрицы и увеличения производительности поиска кривых линий.
При этом отклонение аппроксимирующих отрезков от исходных линий контура, называемое погрешностью аппроксимации
Каждый узел (участок кривой) выражаем через функцию.
При аппроксимации дугами окружностей необходимо определить радиус искомой окружности.
Подобранная (коэффициент детерминации 0,99), нормированная на единичный отрезок [0;1], модельная функция эмпирической зависимости субъективного
Найденная точка максимальной выпуклости эмпирической кривой 76,8 пикс/см отмечена на Рис. 3 вертикальной линией.
Генке «апельсин» — головка таранной кости, которая, по мнению автора, не является отрезком шара, а сдавлена сверху и с медиальной стороны в виде апельсина. Генке линия — межреберная линия (linea intercostalis)...
а) Доказать, что точка T — середина отрезка SM.
Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения данной окружности и проведённой прямой.
– с помощью команды Угол (<Линия>, <Плоскость>) или соответствующего инструмента...
При этом отклонение аппроксимирующих отрезков от исходных линий контура, называемое погрешностью аппроксимации
Каждый узел (участок кривой) выражаем через функцию.
При аппроксимации дугами окружностей необходимо определить радиус искомой окружности.
Генке «апельсин» — головка таранной кости, которая, по мнению автора, не является отрезком шара, а сдавлена сверху и с медиальной стороны в виде апельсина. Генке линия — межреберная линия (linea intercostalis)...











