При разработке конструкции РЭА (радио электронной аппаратуры) необходимо обеспечить требуемую жесткость и механическую прочность ее элементов. Жесткость конструкции есть отношение действующей силы к деформации конструкции, вызванной этой силой.
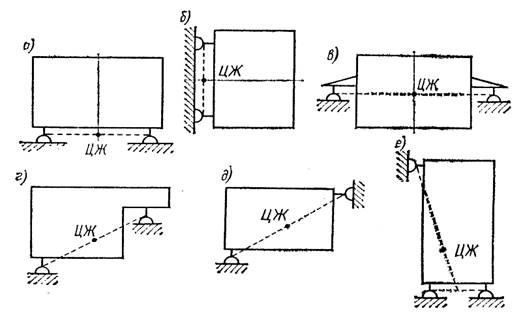
Рис. 1 Основные схемы расположения амортизаторов (в направляющей)
Под прочностью конструкции понимают нагрузку, которую может выдержать конструкция без остаточной деформации или разрушения. Повышение прочности конструкции РЭА связано с усилением ее конструктивной основы, применением ребер жесткости, контровки болтовых соединений и т. д. Особое значение имеет повышение прочности несущих конструкций и входящих в них узлов методами заливки и обволакивания. Заливка пеноматериалом позволяет сделать узел монолитным при незначительном увеличении массы. Во всех случаях нельзя допускать образования механической колебательной системы. Это касается крепления монтажных проводов, микросхем, экранов и других частей, входящих в РЭА. Один из эффективных методов повышения устойчивости конструкции микроэлектронной РЭА, как транспортируемой, так и стационарной, к воздействию вибраций, а также ударных и линейных нагрузок — использование амортизаторов. Действие амортизаторов основано на демпфировании резонансных частот, т. е. поглощении части колебательной энергии. Аппаратура, установленная на амортизаторах, в общем случае может быть представлена в виде механической колебательной системы с шестью степенями свободы: совокупностью связанных колебаний, состоящих из линейных перемещений, и вращательных колебаний по каждой из трех координатных осей. Эффективность амортизации характеризуется коэффициентом динамичности или передачи, числовое значение которого зависит от отношения частоты действующих вибраций f к частоте амортизированной системы fo. При разработке схемы амортизации необходимо стремиться к тому, чтобы система имела минимальное число собственных частот и чтобы они были в 2–3 раза ниже наименьшей частоты возмущающей силы. Для амортизированной аппаратуры следует как можно больше уменьшать собственную частоту, а для неамортизированной, напротив, увеличивать, приближая ее к верхней границе возмущающих воздействий или превышая ее. Проведем анализ динамических коэффициентов для диссипативно неоднородной механической конструкции РЭА, изображенной на рис.2. На рис. 2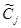 
— операторный жесткости пружинки, который имеет вид (j=1,2,3) [1]
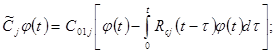(1)
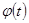— произвольная функция времени; 
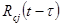— ядро релаксации. Далее, применяя процедуру замораживания [2], заменим соотношения (5) приближенными вида
,
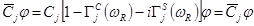где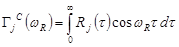 
, 
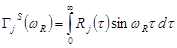, соответственно, косинус и синус — образы Фурье ядра релаксации материала. В качестве примера вязкоупругого материала примем трехпараметрическое ядро релаксации 
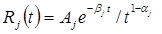, обладающее слабой сингулярностью [3]. Техническая задача состоит в том, чтобы варьируя в физически реализуемых пределах жесткость деформируемого элемента, его размеры и массу, добиться максимального снижения амплитуды резонансных колебаний тела. Исследуются частоты и коэффициенты демпфирования колебаний.
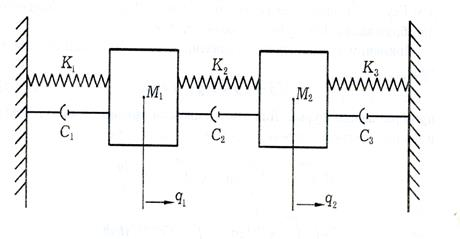
Рис. 2. Расчетная схема
Задача о собственных колебаниях системы, описываемой уравнениями (1)
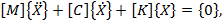(2)
сводится к решению характеристического уравнения
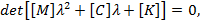
В качестве примера рассмотрим систему с двумя степенями свободы, состоящую из двух тел массой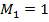 
и M2=0,1 и трех деформируемых элементов с операторными жесткостями 
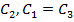(рис.2). Исследуем зависимость собственных частот и коэффициентов демпфирования от мгновенной жесткости 
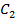при фиксированных значениях 
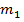и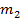 
.
Ядро релаксации принято в виде
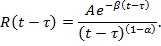
Косинус и синус — образы этого ядра выражаются формулами
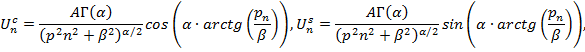
где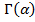
- гамма–функция. Изучены две системы. В первом варианте рассмотрена однородная система, в которой
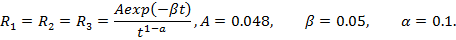
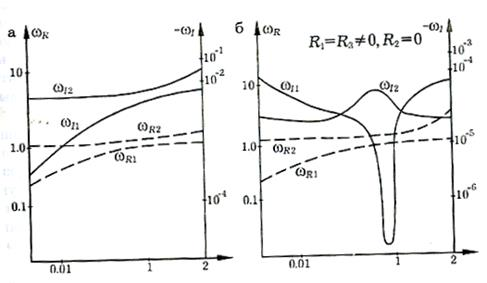
Рис. 3. Зависимость комплексных частот от С2
Результаты расчетов приведены на рис.3, а. Зависимость собственных частот и коэффициентов демпфирования от жесткости С2 оказалась монотонной, причем характер зависимости одинаков для частот, и для коэффициентов демпфирования. Во втором варианте первый демпфирующий элемент упругий (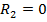
), а остальные элементы совпадают с принятыми выше. Результаты расчета представлены на рис.3, б. Зависимость собственных частот от С2 такая же, как и в случае однородной системы, соответствующие кривые совпадают с точностью до 5 %. Что же касается коэффициентов демпфирования, то их поведение меняется радикальным образом: зависимость 
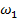от С2 становится немонотонной. Особый интерес представляет минимальное значение коэффициента демпфирования при фиксированной жесткости С2:
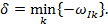
Величина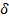 
определяет демпфирующие свойства системы в целом. В случае однородной системы величина С2 (назовем ее глобальным коэффициентом демпфирования) целиком определяется мнимой частью наименьшей по модулю комплексной собственной частоты. В случае неоднородной системы в роли глобального коэффициента демпфирования в зависимости от величины С2 выступают мнимые части как первой, так и второй собственных частот. «Смена ролей» происходит при характерном значении величины С2, когда действительные части первой и второй собственных частот наиболее близки. Глобальный коэффициент демпфирования при указанном характерном значении С2 имеет ярко выраженный максимум. Это обстоятельство представляет, на наш взгляд, новый механический эффект, который может быть сформулирован так: колебания собственных форм неоднородной вязкоупругой системы с близкими частотами взаимно гасят друг друга. Мгновенная жесткость С2 является геометрическим параметром, определяемым размерами элемента, а не физическими свойствами материала. Главная особенность обнаруженного эффекта состоит в качественной зависимости диссипативных свойств системы от ее геометрических параметров. Таким образом, результаты, полученные для рассматриваемой диссипативно неоднородной вязкоупругой конструкции, полностью согласуются с решениями задачи о свободных затухающих колебаниях и подтверждают факт резкого увеличения интенсивности диссипативных процессов при сближении основных частот в неоднородных вязкоупругих системах. При этом роль реологии сводится как к демпфированию колебаний, так и к взаимно усиливающемуся взаимодействию колебаний, различных мод, что существенно повышает диссипативные свойства системы в целом. Данный эффект взаимодействия различных форм движения сплошных тел имеет принципиальную перспективу для синтеза оптимальных по диссипативным свойствам и материалоемкости диссипативно неоднородных машиностроительных конструкций, строительных изделий, демпфирующих компаундов, материалов и композитов различных виброзащитных систем и устройств.
Литература:
1. Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. — Новосибирск: Изд. СО РАН, 1996. — 189 с.
2. Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. — Ташкент: Фан, 1992.
