Модельный оператор, ассоциированный с системой трех частиц на d-мерной решетке рассматривается как тензорная сумма моделей Фридрихса. Найден явный вид существенного и дискретного спектра.
Ключевые слова: модельный оператор, тензорная сумма, модель Фридрихса, определитель Фредгольма, существенный и дискретные спектры.
Пусть 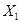 и
и 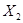 бесконечномерные гильбертовы пространства и
бесконечномерные гильбертовы пространства и 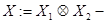 их тензорное произведение. Рассмотрим линейные ограниченные самосопряженные операторы
их тензорное произведение. Рассмотрим линейные ограниченные самосопряженные операторы 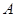 и
и 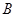 , действующие в
, действующие в 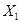 и
и 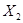 , соответственно. Обозначим через
, соответственно. Обозначим через 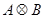 тензорное произведение операторов
тензорное произведение операторов 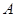 и
и 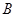 . Оператор
. Оператор 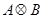 также является линейным ограниченным самосопряженным оператором, действующим в гильбертовом пространстве
также является линейным ограниченным самосопряженным оператором, действующим в гильбертовом пространстве 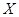 . Положим
. Положим 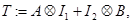 где
где 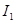 и
и 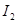 — тождественные операторы в
— тождественные операторы в 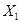 и
и 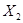 , соответственно. Оператор
, соответственно. Оператор 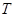 мы будем называть тензорной суммой
мы будем называть тензорной суммой 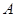 и
и 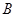 , и будем обозначать через
, и будем обозначать через 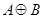 . Оператор
. Оператор 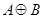 также является линейным ограниченным самосопряженным оператором, действующим в гильбертовом пространстве
также является линейным ограниченным самосопряженным оператором, действующим в гильбертовом пространстве 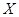 . Для спектра оператора
. Для спектра оператора 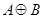 имеет место равенства [1]
имеет место равенства [1]
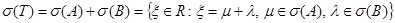 .
.
Очевидно, что если 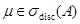 и
и 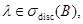 то
то 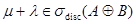 .
.
В моделях физики твердого тела [2,3], а также решетчатой теории поля [4,5] возникают так называемые дискретные операторы Шредингера, являющиеся решетчатым аналогом обычного оператора Шредингера в непрерывном пространстве. Все гамильтонианы этих моделей коммутируют с группой трансляций на решетке. Однако, большое количество интересных задач в физики твердого тела связаны с неидеальными кристаллами, трансляционная инвариантность которых нарушена примесями или дефектами, т. е. один или конечное число узлов решетки оказываются выделенными.
Исследование спектров операторов Шредингера является наиболее интенсивно изучаемым объектом в теории операторов. Одним из важных вопросов в спектральном анализе таких операторов является изучение конечности числа собственных значений, лежащих вне существенного спектра.
В работе [6] изучены спектральные свойства решетчатого гамильтониана 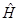 физической системы, состоящей из двух свободных электронов и одной примеси на решетке. Гамильтониан
физической системы, состоящей из двух свободных электронов и одной примеси на решетке. Гамильтониан 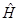 в импульсном представлении действует в тензорном произведении
в импульсном представлении действует в тензорном произведении 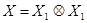 гильбертово пространства
гильбертово пространства 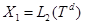 , где
, где 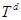 —
— 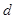 -мерный тор, и он представляется в виде
-мерный тор, и он представляется в виде 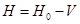 , где
, где 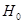 — оператор умножения на функцию
— оператор умножения на функцию 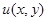 (как невозмущенный оператор), а оператор
(как невозмущенный оператор), а оператор 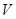 (т. е. некомпактное возмущение) действует по формуле
(т. е. некомпактное возмущение) действует по формуле
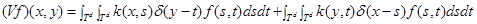 .
.
Здесь 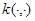 — аналитическая функция на
— аналитическая функция на 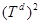 и
и 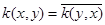 , а
, а 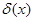 — дельта функция Дирака.
— дельта функция Дирака.
В настоящей работе рассмотрим специальный случай:
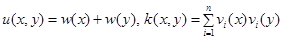 .
.
Данная работа посвящена изучению существенного и дискретного спектров операторов 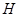 в рассматриваемом специальным случае. С помощью тензорной структуры изучен спектр оператора
в рассматриваемом специальным случае. С помощью тензорной структуры изучен спектр оператора 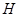 .
.
Пусть 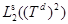 — гильбертово пространство квадратично-интегрируемых симметричных (комплекснозначных) функций, определенньх на
— гильбертово пространство квадратично-интегрируемых симметричных (комплекснозначных) функций, определенньх на 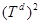 . В гильбертовом пространстве
. В гильбертовом пространстве 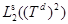 рассмотрим гамильтониан
рассмотрим гамильтониан 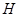 , действующий по формуле
, действующий по формуле
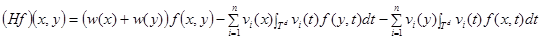 .
.
При этом 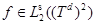 ;
; 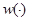 и
и 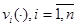 — вещественнозначные непрерывные функции на
— вещественнозначные непрерывные функции на 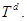 В этих предположениях оператор
В этих предположениях оператор 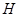 является ограниченным и самосопряженным в
является ограниченным и самосопряженным в 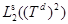 .
.
Наряду с оператором 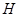 , рассмотрим еще оператор
, рассмотрим еще оператор 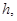 действующий в гильбертовом пространстве
действующий в гильбертовом пространстве 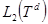 по формуле
по формуле 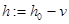 , где
, где
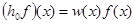 ,
, 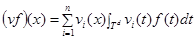 ,
, 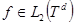 .
.
Из определения операторов 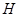 и
и 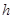 получим, что оператор
получим, что оператор 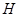 можно представит как тензорная сумма
можно представит как тензорная сумма 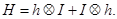 Здесь
Здесь 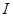 означает тождественный оператор в
означает тождественный оператор в 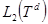 .
.
В данной работе будем изучать спектральные свойства оператора 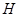 с помощью тензорной суммы операторов.
с помощью тензорной суммы операторов.
Оператор возмущения 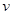 оператора
оператора 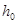 является самосопряженным оператором ранга не более, чем
является самосопряженным оператором ранга не более, чем 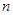 . Из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр
. Из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр 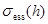 оператора
оператора 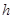 совпадает с существенным спектром оператора
совпадает с существенным спектром оператора 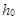 . Известно, что
. Известно, что 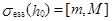 , где числа
, где числа 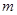 и
и 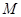 определяются равенствами
определяются равенствами
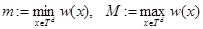 .
.
Из последних двух фактов следует, что 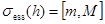 .
.
Определим регулярные в области  функции
функции
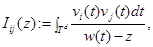
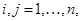
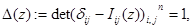
где
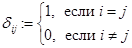 .
.
Видно, что 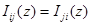 при всех
при всех 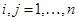 .
.
Установим связь между собственными значениями оператора 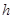 и нулями функции
и нулями функции 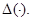
Лемма 1. Число 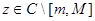 является собственным значением оператора
является собственным значением оператора 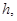 тогда и только тогда, когда
тогда и только тогда, когда 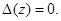
Доказательство. Пусть число 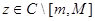 есть собственное значение оператора
есть собственное значение оператора 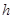 ,
, 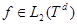 — соответствующая собственная функция. Тогда функция
— соответствующая собственная функция. Тогда функция 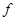 удовлетворяет уравнению
удовлетворяет уравнению
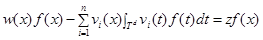 . (1)
. (1)
Заметим, что для любых 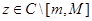 имеет место соотношение
имеет место соотношение 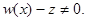 Тогда из уравнения (1) для
Тогда из уравнения (1) для 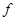 имеем
имеем
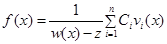 , (2)
, (2)
где
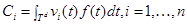 . (3)
. (3)
Подставляя выражение (2) для 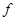 в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда система
в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда система 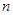 линейных уравнений с
линейных уравнений с 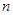 неизвестными
неизвестными
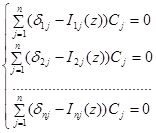
имеют ненулевое решение 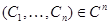 , т. е. когда
, т. е. когда 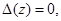 где
где 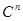 - декартова
- декартова 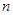 -ная степень множества
-ная степень множества 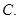 Лемма 1 доказана.
Лемма 1 доказана.
Из леммы 1 вытекает, что имеет место равенство
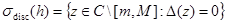 .
.
Следовательно, функция 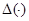 является определителем Фредгольма, ассоциированным с оператором
является определителем Фредгольма, ассоциированным с оператором 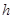 .
.
Для любого 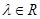 и ограниченного самосопряженного оператора
и ограниченного самосопряженного оператора 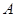 , действующего в гильбертовом пространстве
, действующего в гильбертовом пространстве 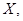 обозначим через
обозначим через 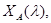 такое подпространство, что
такое подпространство, что 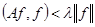 для любого
для любого 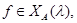 и положим
и положим 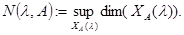 Число
Число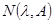 равно бесконечности, если
равно бесконечности, если 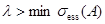 и если число
и если число 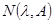 конечно, то оно равно числу собственных значений оператора
конечно, то оно равно числу собственных значений оператора 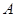 (с учетом кратности), меньших чем
(с учетом кратности), меньших чем 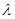 .
.
Следующая лемма описывает число и местонахождение собственных значений оператора 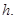
Лемма 2. Оператор 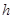 может иметь не более чем п собственных значений (с учетом кратности), лежащих левее
может иметь не более чем п собственных значений (с учетом кратности), лежащих левее 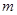 и не имеет собственных значений, лежащих правее
и не имеет собственных значений, лежащих правее 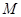 .
.
Доказательство. Так как 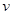 является
является 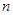 -мерным оператором, в силу теоремы 9.3.3 из книги [7] имеем
-мерным оператором, в силу теоремы 9.3.3 из книги [7] имеем
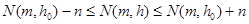 ,
,
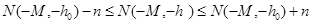 .
.
Учитывая равенство 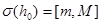 , получим, что
, получим, что 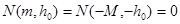 . Следовательно,
. Следовательно, 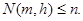
Из 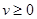 следует, что при всех
следует, что при всех 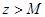 и
и 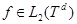 имеет место cоотношение
имеет место cоотношение
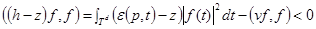 .
.
Это означает, что оператор 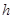 не имеет собственных значений, лежащих правее
не имеет собственных значений, лежащих правее 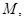 т. е.
т. е. 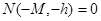 . Лемма 2 доказана.
. Лемма 2 доказана.
Теперь сформулируем основной результат работы.
Теорема 1. а) Если 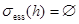 , то
, то 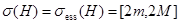 .
.
б) Пусть 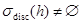 . Предположим, что
. Предположим, что 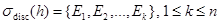 . Тогда имеет место равенства
. Тогда имеет место равенства
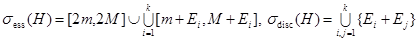 .
.
Доказательство. Как отметили выше из определения операторов 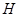 и
и 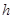 получим, что оператор
получим, что оператор 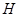 можно представит как тензорная сумма
можно представит как тензорная сумма 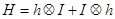 . Поэтому для спектра оператора
. Поэтому для спектра оператора 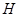 имеем
имеем
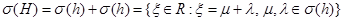 . (4)
. (4)
Если 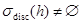 , и следовательно,
, и следовательно, 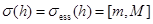 , то
, то 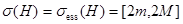 .
.
Пусть теперь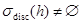 . По предположению
. По предположению 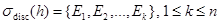 . Теперь соотношение (4) завершает доказательство теоремы 1.
. Теперь соотношение (4) завершает доказательство теоремы 1.
Из утверждения б) теоремы 1 следует, что множество 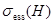 представляет собой объединение не более чем
представляет собой объединение не более чем 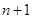 отрезков, а число собственных значений (с учетом кратности) не превосходит чем
отрезков, а число собственных значений (с учетом кратности) не превосходит чем 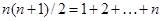 , т. е.
, т. е. 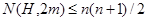 .
.
Литература:
1. М. Рид, Б. Саймон, Методы современной математической физики, т. 4. Анализ операторов, М.: Мир. 1982.
2. D. C. Mattis. The few-body problem on lattice // Rev.Modern Phys., — 1986, — V. 58, P. 361–379.
3. A. I. Mogilner. Hamiltonians in solid state physics as multiparticle discrete Schroedinger operators: problems and results // Advances in Sov. Math., — 1991, — V. 5, P. 139–194.
4. В. А. Малышев, Р. А. Минлос. Кластеpные опеpатоpы // Тpуды семинаpа им. И. Г. Петpовского. — 1983, — Вып. 9, С. 63–80.
5. С. Н. Лакаев, Р. А. Минлос. О связанных состояниях кластерного оператора. Теоретическая и математическая физика, — 1979, — Т. 39, С. 83–92.
6. Ю. Х. Эшкабилов. Об одном некомпактном возмущении в непрерывном спектре оператора умножения на функцию // Узб. матем. журнал, — 2003, — № 1, С. 81–88.
7. М. Ш. Бирман, М. З. Саломяк, Спектральная теория самосопряженных операторов в гильбертовом пространстве. Издательство ЛГУ, Ленинград, 1980.







