В работе рассматривается модельный дискретный оператор Шредингера 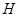 описывающий системы трех квантовых частиц, движущихся на одномерной решетке и взаимодействующих с помощью парных нелокальных потенциалов. Построен аналог системы интегральных уравнений Фаддеева для собственных функций оператора
описывающий системы трех квантовых частиц, движущихся на одномерной решетке и взаимодействующих с помощью парных нелокальных потенциалов. Построен аналог системы интегральных уравнений Фаддеева для собственных функций оператора 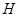 .
.
Ключевые слова: дискретный оператор Шредингера, нелокальный потенциал, уравнение Фаддеева, операторное уравнение, определитель Фредгольма, класс Гильберта-Шмидта.
Исследованию существенного спектра непрерывных и дискретных операторов Шредингера посвящены многие работы (см. например [1,2] и [3,4], соответственно). При этом один из основных инструментов при изучении существенного и дискретного спектра многочастичного оператора Шредингера является аналог уравнения Фаддеева и его симметризованный вариант. Заметим, что потенциалы, рассматриваемые в работах [3,4] являются локальными, т. е. операторами умножения на функцию в координатном представлении.
В настоящей статье изучен модельный дискретный оператор Шредингера 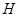 описывающий системы трех квантовых частиц, движущихся на одномерной решетке и взаимодействующих с помощью парных нелокальных потенциалов [1,2]. Отметим, что для многочастичных гамильтонианов нелокальные потенциалы в импульсном представлении являются частично-интегральными операторами. Построен аналог системы интегральных уравнений Фаддеева для собственных функций оператора
описывающий системы трех квантовых частиц, движущихся на одномерной решетке и взаимодействующих с помощью парных нелокальных потенциалов [1,2]. Отметим, что для многочастичных гамильтонианов нелокальные потенциалы в импульсном представлении являются частично-интегральными операторами. Построен аналог системы интегральных уравнений Фаддеева для собственных функций оператора 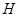 .
.
Пусть 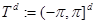 —
— 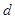 -мерный тор с соответствующим отождествлением противоположных граней и
-мерный тор с соответствующим отождествлением противоположных граней и 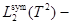 гильбертово пространство квадратично-интегрируемых (комплекснозначных) симметричных функций, определенных на
гильбертово пространство квадратично-интегрируемых (комплекснозначных) симметричных функций, определенных на 
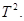
В гильбертовом пространстве 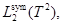 рассмотрим модельный дискретный оператор Шредингера
рассмотрим модельный дискретный оператор Шредингера 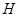 действующий по формуле
действующий по формуле

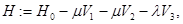
где 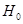 — оператор умножения на функцию
— оператор умножения на функцию 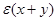 в
в 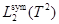 :
:
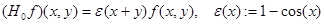 ,
,
a 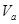 ,
, 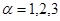 — нелокальные операторы взаимодействия вида
— нелокальные операторы взаимодействия вида
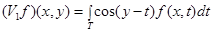 ,
, 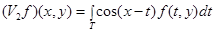 ,
,
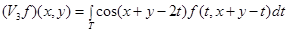 .
.
Здесь 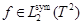 и
и 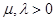 произвольные вещественные постоянные.
произвольные вещественные постоянные.
При этих предположениях оператор 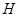 является ограниченным и самосопряженным в гильбертовом пространстве
является ограниченным и самосопряженным в гильбертовом пространстве 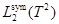 .
.
Приведем несколько основных обозначений, которые будут применяться на работе. При каждом фиксированном 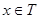 определим регулярные в области
определим регулярные в области 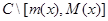 функцию
функцию

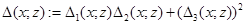 ,
,
где функции 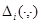 ,
, 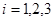 определены следующим образом:
определены следующим образом:
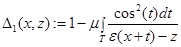 ,
, 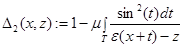 ,
, 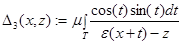 ,
,
а числа 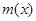 и
и 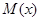 определяются равенствами
определяются равенствами
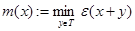 ,
, 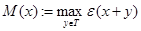 .
.
Пусть 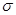 — множество тех точек
— множество тех точек 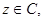 для которых равенство
для которых равенство 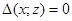 имеет место хотя бы для одной
имеет место хотя бы для одной 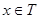 и
и 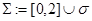 . Обозначим через
. Обозначим через 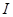 единичный оператор в
единичный оператор в 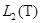 и положим
и положим
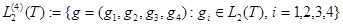 ,
, 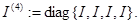
При каждом 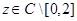 вводим блочно-операторные матрицы (размера
вводим блочно-операторные матрицы (размера 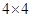 )
) 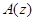 и
и 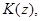 действующие в пространстве
действующие в пространстве 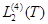 по формулам
по формулам
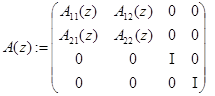 и
и 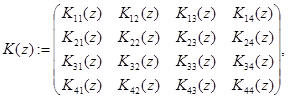
где 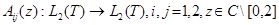 — оператор умножения на функцию
— оператор умножения на функцию 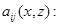
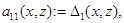
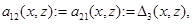
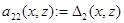 ,
,
а операторы 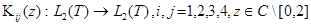 — интегральные операторы с ядрами
— интегральные операторы с ядрами 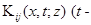 переменная интегрирования)
переменная интегрирования)
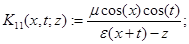
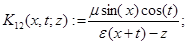
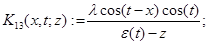
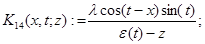
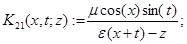
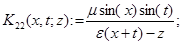
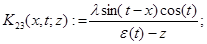
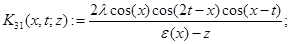
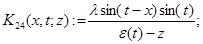
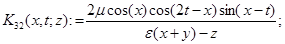
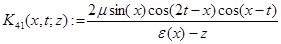 ,
, 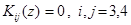 .
.
Заметим, что при каждом 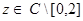 интегральные операторы
интегральные операторы 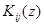 принадлежат классу Гильберта-Шмидта, следовательно,
принадлежат классу Гильберта-Шмидта, следовательно, 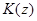 является компактным оператором.
является компактным оператором.
Отметим, что при каждом 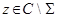 оператор
оператор 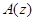 обратим, поэтому для таких
обратим, поэтому для таких 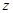 мы можем определить оператор вида
мы можем определить оператор вида 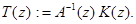
Следующая теорема устанавливает связь между собственными значениями операторов 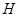 и
и 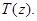
Теорема 1. Число 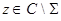 является собственным значением оператора
является собственным значением оператора 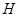 тогда и только тогда, когда оператор
тогда и только тогда, когда оператор 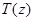 имеет собственное значение, равное единице, и их кратности совпадают.
имеет собственное значение, равное единице, и их кратности совпадают.
Доказательство. Пусть 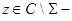 собственное значение оператора
собственное значение оператора 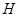 и
и 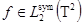 — соответствующая собственная функция. Тогда функция
— соответствующая собственная функция. Тогда функция 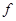 удовлетворяет уравнению
удовлетворяет уравнению 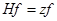 или
или
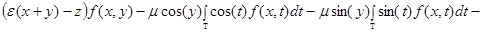
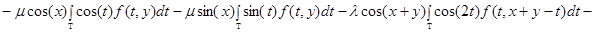
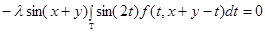 . (1)
. (1)
Так как 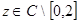 , при всех
, при всех 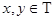 имеет место соотношение
имеет место соотношение 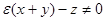 . Поэтому из уравнения (1) для
. Поэтому из уравнения (1) для 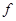 имеем равенство
имеем равенство

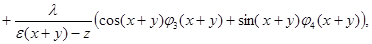 (2)
(2)
где
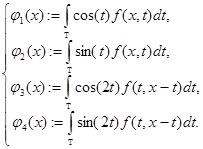 (3)
(3)
Подставляя выражение (2) для 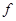 в системе обозначений (3), получим, что система уравнений
в системе обозначений (3), получим, что система уравнений
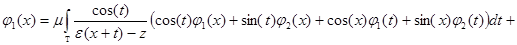
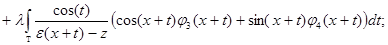
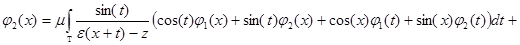
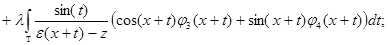
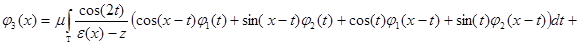
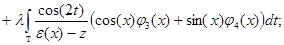
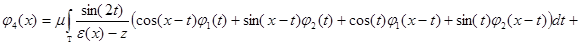
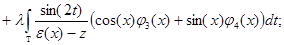
или
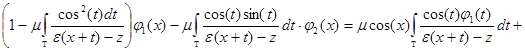
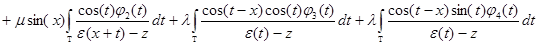 ;
;
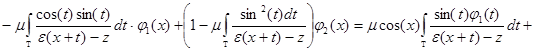
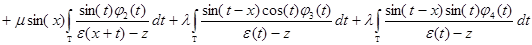 ;
;
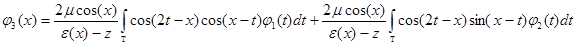 ;
;
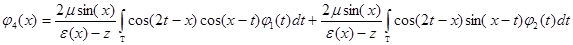 .
.
или же матричное уравнение
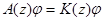 (4)
(4)
имеет нетривиальное решение тогда и только тогда, когда уравнение (1) имеет нетривиальное решение и линейные подпространства, порожденные решениями уравнений (1) и (4), имеют одинаковые размерности.
При каждом 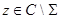 оператор
оператор 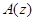 обратим, и следовательно, уравнение
обратим, и следовательно, уравнение 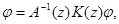 т. е. уравнение
т. е. уравнение 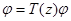 имеет нетривиальное решение тогда и только тогда, когда уравнение (4) имеет нетривиальное решение. Здесь также линейные подпространства, порожденные решениями уравнений (4) и
имеет нетривиальное решение тогда и только тогда, когда уравнение (4) имеет нетривиальное решение. Здесь также линейные подпространства, порожденные решениями уравнений (4) и 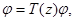 имеют одинаковые размерности. Теорема доказана.
имеют одинаковые размерности. Теорема доказана.
Замечание. Отметим, что операторное уравнение 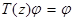 обычно называется аналогом уравнения Фаддеева для собственных функций оператора
обычно называется аналогом уравнения Фаддеева для собственных функций оператора 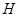 .
.
Один из важных применений уравнения Фаддеева 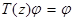 для собственных функций оператора
для собственных функций оператора 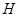 можно видит при доказательстве включение
можно видит при доказательстве включение 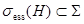 , см. [4]. Ещё другое важное применение симметричного варианта этого уравнения можно наблюдать при доказательстве конечности или бесконечности дискретного спектра оператора
, см. [4]. Ещё другое важное применение симметричного варианта этого уравнения можно наблюдать при доказательстве конечности или бесконечности дискретного спектра оператора 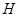 .
.
Литература:
1. М. Рид, Б. Саймон. Методы современной математической физики. Т. 4. Анализ операторов, Москва: Мир, 1982 г.
2. Г. М. Жислин. Исследование спектра оператора Шредингера для системы многих частиц // Труды Московского математического общества. — 1960, — V. 9, — C. 81–120.
3. S. Albeverio, S. N. Lakaev, Z. I. Muminov. Schroedinger operators on lattices. The Efimov effect and discrete spectrum asymptotics // Ann. Henri Poincare. — 2004, — V. 5, — P. 743–772.
4. С. Н. Лакаев, М. Э. Муминов. Существенный и дискретный спектр трехчастичного оператора Шредингера на решетке // Теоретическая и математическая физика, — 2003, — Т. 135, — № 3, С. 478–503.







