Одной из основных целей модернизации высшего образования на современном этапе заключается в повышении качества подготовки специалистов. С этой целью в процесс обучения введена модульно-рейтинговая технология, основной составляющей которой является рейтинг-контроль, предусматривающий дифференцированный подход к контролю знаний студентов. Контроль может быть организован традиционным способом в виде контрольной или зачетной работы, либо в виде тестирования. Такой контроль обладает рядом преимуществ:
1) объективность (исключается фактор субъективного подхода со стороны преподавателя);
2) валидность (большое количество заданий теста охватывает весь объем изучаемого курса);
3) простота (тестовые задания конкретнее и лаконичнее заданий контрольной работы и не требуют развернутого ответа или обоснования);
4) демократичность (все тестируемые находятся в равных условиях);
5) массовость (возможность за определенный промежуток времени проверить у большего количества студентов уровень усвоения основных дидактических единиц модуля);
6) технологичность (простота подведения результатов) [3].
Рассмотрим тесты контроля по теме «Обыкновенные дифференциальные уравнения». Тесты трехуровневые, включающиеся в себя репродуктивные и продуктивные задания, а также задания разного типа.
Тесты контроля применяются или до, или после изучения понятий, теорем или темы в целом. Если тесты применяются до изучения темы (понятия, теоремы), то с их помощью определяется уровень сформированных действий, необходимых для изучения новой темы. Тесты, применяемые после изучения темы (понятия, теоремы), контролируют действия, сформированные в процессе изучения темы, раздела, всего курса обучения учебному предмету [4].
Тест содержит задания на опознание, на различение и на соотнесение. Такие, как:
1. Уравнение 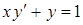 …является…
…является…
1) однородным относительно 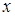 и
и 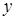 дифференциальным уравнением первого порядка;
дифференциальным уравнением первого порядка;
2) уравнением Бернулли;
3) уравнением с разделяющимися переменными;
4) линейным неоднородным дифференциальным уравнением 2-го порядка.
2. Уравнение 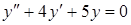 является…
является…
1) линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами;
2) уравнением Бернулли;
3) линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами;
4) дифференциальным уравнением с разделяющимися переменными.
3. Однородным дифференциальным уравнением первого порядка являются дифференциальные уравнения…
1) 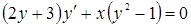 ; 2)
; 2) 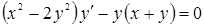 ;
;
3) 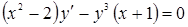 ; 4)
; 4) 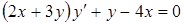 .
.
Приведенные выше задания позволяют выявить уровень пассивного овладения материалом, для которого характерно овладение отдельно взятым действием.
Тест также содержит задания конструктивного типа и типовые задачи:
1. Общее решение дифференциального уравнения 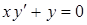 имеет вид…
имеет вид…
1) 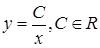 ; 2)
; 2) 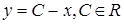 ;
;
3) 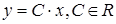 ; 4)
; 4)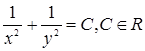 .
.
2. Общее решение линейного однородного дифференциального уравнения второго порядка 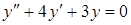 имеет вид…
имеет вид…
1) 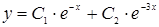 ; 2)
; 2) 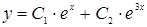 ;
;
3) 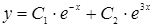 ; 4)
; 4) 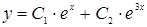 .
.
3. Общий вид частного решения 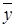 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 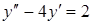 будет выглядеть так…
будет выглядеть так…
1) 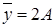 ; 2)
; 2) 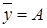 ; 3)
; 3) 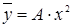 ; 4)
; 4) 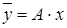 .
.
4. Решение задачи Коши 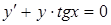 ,
, 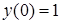 имеет вид…
имеет вид…
1) 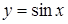 ; 2)
; 2) 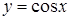 ; 3)
; 3) 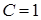 ; 4)
; 4) 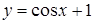 .
.
Правильно выполненные задания данного типа указывают на овладение более сложным действием, составленным из нескольких действий, и на способность применения сложного действия в алгоритмической ситуации.
Следующие задания теста предполагают определенный уровень овладения теоретической базой и умение применять её на практике. Они характеризуются овладением сложным действием, способностью применения этого действия вне алгоритмических ситуаций, а также свободное оперирование действиями, адекватными понятию или теореме.
1. Общее решение системы дифференциальных уравнений
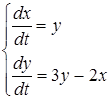 имеет вид…
имеет вид…
1) 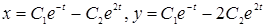 ;
;
2) 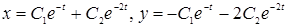 ;
;
3) 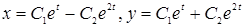 ;
;
4) 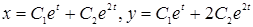 .
.
2. Установите соответствие между дифференциальным уравнением второго порядка и его общим решением
1) 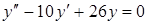 ; А)
; А) 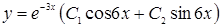 ;
;
2) 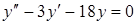 ; В)
; В) 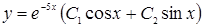 ;
;
3) 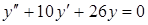 . С)
. С) 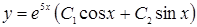 ;
;
D) 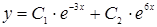 .
.
Анализируя результаты тестирования, выявляется уровень освоения темы. Всего выделяются четыре уровня.
Первый уровень свидетельствует об усвоении элементарных понятий. Допущенные ошибки, показывают, что студенты не овладели системой знаний по теме.
Второго уровня достигают студенты, которые обладают основными знаниями и умениями и могут применить их для решения простейших задач.
Третий уровень демонстрируют студенты, которые овладели учебным материалом и у них сформированы основные умения, соответствующие изученной теме. Они могут анализировать, сравнивать и обоснованно выбирать методы решения стандартных задач.
Самый высокий — четвертый уровень. Студенты, достигшие этого уровня способны успешно применять полученные знания для поиска решений и исследований в нестандартных практико-ориентированных задачах. Данный уровень является основой для формирования профессиональных компетенций.
Для своевременного выявления уровня овладения студентом учебного материала тесты используются не только на итоговых этапах изучения модуля, но в процессе его изучения как средство диагностики и управления учебной деятельностью.
Тесты, с помощью которых проверяется уровень усвоения модуля, являются инструментом, который обеспечивают управление процессом обучения, так как позволяют оперативно и объективно получать, оценивать и анализировать уровень усвоения знаний и способствуют переходу обучаемых с одного уровня усвоения знаний и сформированности умений на другой, более высокий. Это свидетельствует о повышении качества подготовки высококвалифицированных специалистов в рамах модульно-рейтинговой системы обучения.
Литература:
1. Гудкова В. С., Ячинова С. Н. Пути повышения качества обучения математике студентов технических вузов // Молодой ученый. — 2015. — № 3 (83). — С. 755–758.
2. Гудкова В. С., Ячинова С. Н. Пути повышения качества обучения математике студентов экономических специальностей // Молодой ученый. — 2015. — № 6 (86). — С. 584–588.
3. Круглова А. Н., Ячинова С. Н. Методические аспекты тестирования как одной из форм итогового контроля // Новый университет. — 2013. — № 10 (31). — С. 4–8.
4. Новичкова Т. Ю., Гудкова В. С., Ячинова С. Н. Современные средства оценивания результатов обучения // Молодой ученый. — 2014. — № 6 (65). — С. 740–742.
5. Новичкова Т. Ю., Хвастунова Е. М., Ячинова С. Н. Критериальные задания как фактор совершенствования процесса обучения математике // Вестник магистратуры. — 2014. — № 6–1 (33). — С.125–127.
6. Новичкова Т. Ю., Хвастунова Е. М., Ячинова С. Н. Взаимосвязь этапов развития математики и тестирования // Вестник магистратуры. — 2014. — № 8 (35). — С.56–58.
7. Ячинова С. Н. Цели обучения как средство управления учебной деятельностью на уроке математики // Дис. канд. пед наук — Пенза, 2003. — 165с.







