Дается краткий анализ формирования олимпийского движения, вызванного заинтересованностью в нем спортсменов и общества. На основе анализа статистических данных предлагаются модели формирования спортивных групп, представленных задачами Коши для обыкновенных дифференциальных уравнений. Исследуется устойчивость стационарных состояний и поведение решений при различных значениях параметров.
Ключевые слова: популяция, математическое моделирование, спортивные достижения, олимпийское движение.
Введение. Физическая культура начала формироваться на ранних этапах организации общества. Об этом свидетельствуют различные источники информации в виде наскальных рисунков, росписей глиняной посуды, статуэток и из иных, дошедших до нас из доисторических времен свидетельств [14, 16, 31, 34, 51, 53, 58, 60]. В VI — II тысячелетиях в различных городах и государствах возникают спортивные школы, развивающие свои виды спорта, проводятся спортивные соревнования [34]. Наивысшая организация физической культуры и спорта была достигнута в античной Греции. В IX — VIII вв. до н. э. сформировалась эллинистическая система физического воспитания с правилами проведения спортивной подготовки и судейства соревнований [34]. В основе лежали такие виды спорта как гимнастика, бег, метание снарядов, борьба, кулачные бои. Строились спортивные сооружения: стадионы, спортивные площадки и залы. Система физического воспитания постепенно распространялась на школьное образование [34]. Сформировался «симбиоз» государственных институтов, спортсменов и зрителей, результатом которого стала организация спортивных соревнований с награждением победителей. Наиболее популярными стали Олимпийские игры, на которых, начиная с 776 года до н. э. и вплоть до 394 год н. э., победители награждались и их имена фиксировались [34]. Такие мероприятия и сегодня являются формой привлечения молодежи в сферу физического воспитания.
Попытки возродить Олимпийские игры, запрещенные в 394 году н. э. [34], на межгосударственном уровне стали предприниматься в начале XIX. Однако понадобилось около 50 лет усилий общественных деятелей, прежде чем в 1894 году было принято решение о создании Олимпийского комитета и организации проведения в 1896 году первых Олимпийских игр. Следующим важнейшим шагом было принятие решения о проведении самостоятельной зимней Олимпиады в 1924 году. Дальнейшее развитие спортивного олимпийского движения шла по пути создания Национальных олимпийских комитетов, увеличения олимпийских видов спорта и привлечения большего числа спортсменов в олимпийское движение [34]. Массовость спортивного движения, как следствие организационной, просветительной и агитационной деятельности международного и национальных олимпийских комитетов, привела к созданию спортивных сооружений, учебных заведений и медицинских учреждений, организации производства спортивного инвентаря и снаряжения. Таким образом, основным механизмом, направленным на развитие системы олимпийского движения современности также как и в античной Греции, остается «активный» симбиоз органов управления, общественности и участников спортивного движения.
В современном мире олимпийское движение играет немаловажную роль в развитии спорта во всех странах. Оно находит поддержку во всех слоях общества. Тем не менее, для его устойчивого развития необходимы как моральная поддержка общества, так и независимая финансовая поддержка. При отсутствии надежной финансовой базы олимпийское движение утрачивает свою независимость, экономическую самостоятельность. Основой финансовой безопасности и независимости стал олимпийский маркетинг [41, 47, 49], позволяющий уйти от влияния как государственных, так и частных организаций. У олимпийского маркетинга две основные программы — партнерство с телерадиовещательными компаниями (50 % материальных ресурсов) и спонсорство (40 % ресурсов). Сегодняшняя система телерадиовещания охватывает около половины жителей Земли. Через многочисленные спортивные программы повышается интерес у граждан к активному занятию спортом. Спонсоры в виде частных лиц, обществ, организаций и различных компаний своим вкладом в олимпийские мероприятия также привлекают новых участников в спортивное движение. Таким образом, сегодняшний симбиоз «олимпийское движение — общество» основан на повышении интереса к спортивному движению у граждан, а не на экономической основе.
Современная система подготовки спортсменов представлена различными спортивными обществами, школами, секциями, отдельными группами и командами с постоянным межгрупповым обменом спортсменами [2, 4, 6, 18, 19, 52, 55, 57]. В объединениях спортсменов также формируется спортивная мотивация, направленная на привлечение молодежи к занятиям спортом, на совершенствование мастерства спортсменов [3, 8, 9, 10, 15, 17, 22, 35, 39, 40, 42, 45, 56, 55, 59]. С учетом этого разрабатываются и стратегии развития спортивных организаций [33, 37, 38].
В математических моделях взаимодействующих популяций учитываются различные взаимоотношения между ними: конкуренция, симбиоз, хищничество [1, 5, 11, 13, 24, 26 — 29, 32]. Однако, в этих моделях не учитывается межличностный характер взаимоотношений ни между особями, ни между их группами. В социальной самоорганизации определяющим является доминирующая идея, вызывающая активность членов социума [25, 43].
Динамика основных показателей спортивного движения. К основным количественным показателям можно отнести число стран участников олимпийского движения, число спортсменов, принявших участие в соревнованиях и динамику роста рекордов спортсменов. На рис. 1 отражено изменение числа стран участниц всех олимпиад современности, на рис. 2 — числа спортсменов, участвовавших в олимпиадах, а на рис. 3 — числа спортсменов участников зимних олимпиад (все статистические данные отмечены символом 
). Уменьшение числа спортсменов, участвовавших в олимпиаде 1932 года, объясняется мировым экономическим кризисом, а в 1980 — бойкотом олимпиады со стороны некоторых стран. Число спортсменов-участников летних олимпиад выросло с 246 в 1896 году до 10919 в 2012 году (рис. 2), а зимних с 301 в 1924 году до 2876 в 2010 году (рис. 3). Наряду с ростом числа участников олимпиад растут и рекордные результаты спортсменов. Так, например, на рис. 4 отражено изменение рекордов в фигурном катании с 1896 по 2014 гг., под которыми понимается число новых «оборотов», достигнутых спортсменами к текущему моменту времени.
Динамика изменения этих показателей достаточно хорошо описывается уравнением [5, 11, 13, 24, 26 — 28, 32]
,
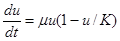в котором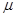 
— удельная скорость роста, а 
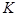— постоянная, называемая в моделях популяционной биологии емкостью среды [5]. На рис 1 — 4 расчетным зависимостям соответствуют сплошные линии с 
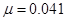для динамики стран участниц олимпиад (рис. 1), с 
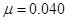для числа спортсменов на летних олимпиадах (рис. 2), с 
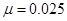для спортсменов участников зимних олимпиад (рис. 3) и с 
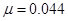для числа «рекордов» в фигурном катании (рис. 4). Для аппроксимации статистических данных использовались алгоритмы, включающие в себя численные методы решения задачи Коши для обыкновенных дифференциальных уравнений [30, 54] и методы минимизации функционалов [20, 21, 23, 36, 46, 48, 61].
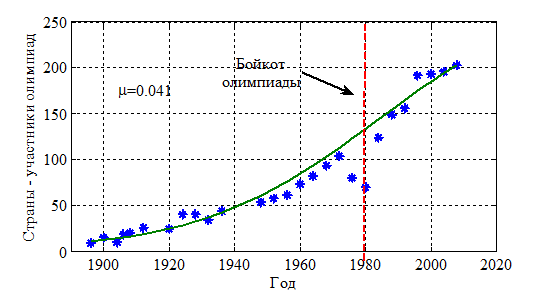
Рис. 1.
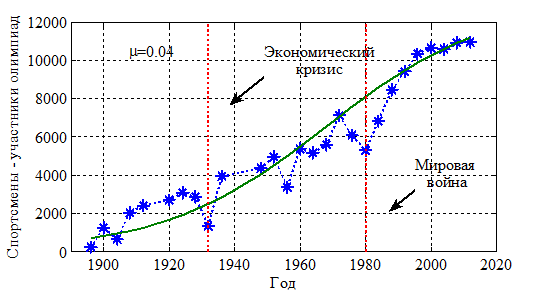
Рис. 2.
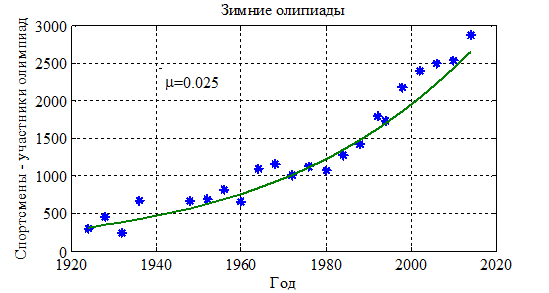
Рис. 3.
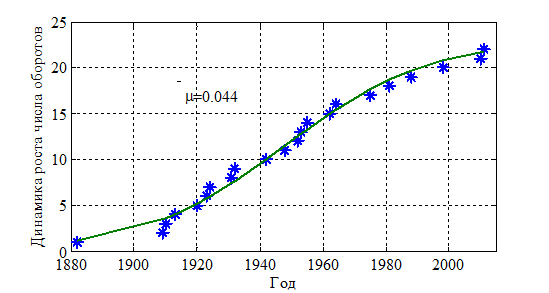
Рис. 4.
Математическая модель образования спортивной группы. Как следует из анализа развития на протяжении многих столетий спортивного движения оценить все факторы, влияющие на динамику изменения числа соревнований и количества участников, не представляется возможным. Влияние общества на формирование групп многогранно. Поэтому, как это предлагается в [25], в модель вводится «индекс активности общества»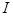 
, который должен зависеть от уровня вовлечения в спортивную группу новых участников. Поскольку в спортивном движении «движущей» силой является мотивация, а не экономическая составляющая, то последняя, как это предлагается в [7, 12, 23, 44, 50], в модели не учитывается.
Пусть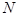 
— число лиц, объединившихся в группу, а 
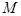— число лиц, которые желают стать участниками группы. Примем, что общее их количества равно единице: 
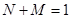. Примем, что скорость убыли участников группы пропорциональна их количеству, а скорость их увеличения — числу участников группы, числу желающих в ней участвовать и индексу активности. При этом индекс активности должен уменьшаться после наполнения группы до определенного уровня. Тогда модель формирования группы, с учетом равенства 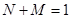, представлена системой двух дифференциальных уравнений
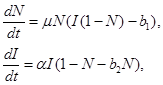(1)
где ,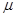 
, 
, 
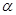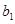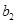— положительные постоянные.
В этой системе уравнений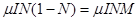 
— скорость наполнения группы, 
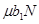— скорость убыли участников группы. Во втором уравнении учтено, что «активность» вовлечения новых участников группы начнет уменьшаться, если ее численность превысит значение 
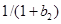. В этой модели учитывается то, что скорость роста числа участников группы и «индекса активности» в первом приближении пропорциональны численности участников (рис. 2 — 3) и «активности властей» (рис. 1).
Система уравнений (1) имеет две стационарные точки: тривиальную и нетривиальную. В тривиальной стационарной точке матрица Якоби правой части уравнений (1) имеет положительное собственное значение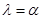 
и, соответственно, эта стационарная точка неустойчивая.
Во второй стационарной точке
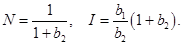
Собственные значения матрицы Якоби
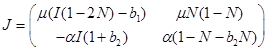
в этой стационарной точки
, 
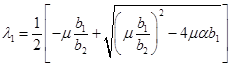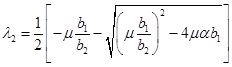
будут отрицательными, если выполняется неравенство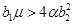 
, и комплексно сопряженными с отрицательной вещественной частью, если выполняется неравенство 
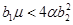. То есть эта стационарная точка будет устойчивой.
Затухающие колебания возникают при выполнении неравенства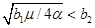 
. То есть в том случае, если «емкость группы», а в рассматриваемой модели она равна 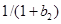, будет низкой при малой скорости уменьшения численности группы (при малых значениях 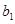по сравнению с 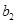). На рис. 5 для случая 
, 
, 
, 
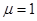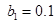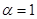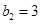показаны зависимост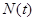и 
и 
. Собственные значения матрицы Якоби при этих значениях параметров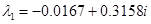 
и 
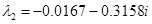комплексно сопряженные. Рассмотренный пример соответствует случаю, когда первоначальная численность группы мала (
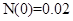) и низка «активности» общества (
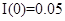). Сначала происходит медленное увеличение численности группы и более быстрое увеличение индекса активности. По мере увеличения численности группы начинает снижаться «активность», затем с небольшим опозданием начинает уменьшаться и численность группы. Возникающие колебания являются затухающими — значения функций постепенно будут приближаться к их стационарным значениям.
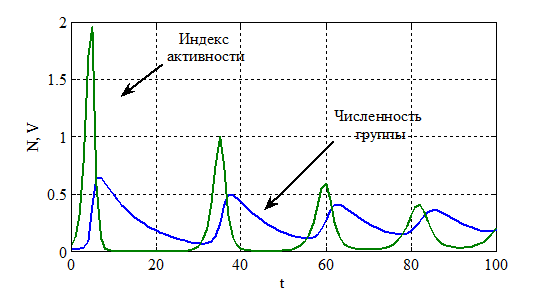
Рис. 5.
Модель двух взаимодействующих групп. На территориях могут существовать несколько групп лиц, занимающихся конкретным видом спорта [4, 6, 38, 52, 57]. Контакт между группами может сопровождаться переходом спортсменов из одной группы в другую [57, 59]. Примером могут служить лиги игровых видов спорта, между которыми всегда происходит обмен спортсменами (например, футбол, баскетбол). В детских спортивных школах группы комплектуются по возрастному принципу [35, 52]. В таких школах наиболее подготовленные участники переводятся в старшую возрастную группу, а менее подготовленные — в младшую.
Пусть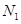 
— число лиц, объединившихся в первую группу, а 
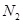— число лиц, объединившихся во вторую группу; 
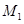— число лиц, которые желают стать участниками первой группы, 
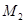— второй группы; 
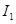— индекс активности для первой группы, а 
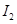— для второй. Пусть 
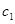— скорость перехода участников первой группы во вторую, а 
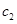— участников второй группы в первую. С учетом этих предположений модель (1) для случая двух групп принимает вид
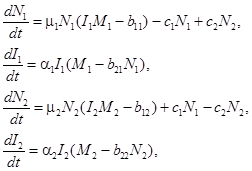(2)
где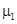 
, 
, 
, 
, 
, 
, 
, 
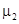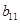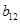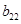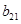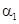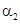— положительные постоянные.
Система уравнений (2) имеет две стационарные точки
, 
, 
, 
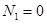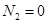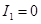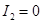
и
.
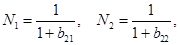
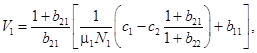
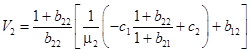В первой стационарной точке матрица Якоби правой части уравнений (2) имеет два положительных собственных значения. Поэтому эта стационарная точка будет неустойчивой. Вторая стационарной точке является устойчивой.
В модели (2) стационарные значения численностей групп такие же, как и в модели (1). Отличие состоит в скорости достижения стационарных состояний. Так, например, для случая констант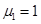 
, 
, 
, 
, 
, 
, 
, 
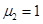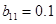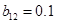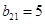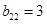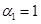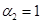на рис. 6а показаны зависимости 
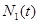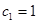при 
и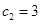 
, а также при 
, 
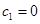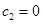, а на рис. 6б — зависимости 
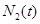. Как следует из этих результатов при взаимодействии двух групп с переходом спортсменов из одной группы в другую, а этот можно интерпретировать как «обмен опытом», стационарные состояния могут достигаться быстрее, чем при отсутствии переходов.
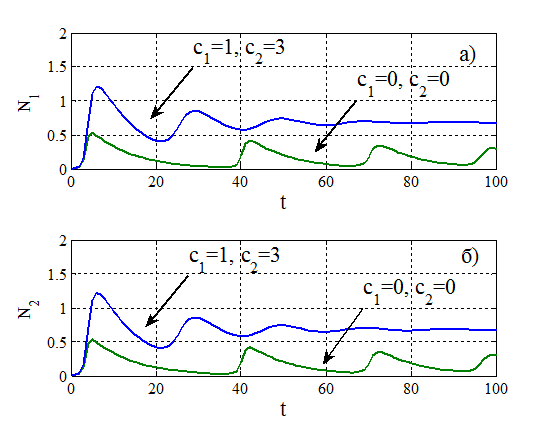
Рис. 6.
Модель, учитывающая спортивные достижения. После проведение больших спортивных соревнований с широким освещением «физических» и «моральных» успехов спортсменов как в личных, так и в командных соревнованиях возрастает число желающих заниматься спортом [34, 43]. Рекордные результаты становятся мотивационным фактором для занятий спортом. В математической модели (1) это можно учесть, введя уравнение для количества рекордов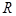 
, влияющих на индекс активности
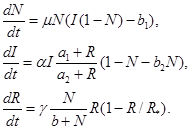(3)
В третьем уравнении функция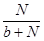 
отражает тот факт, что скорость роста числа рекордов пропорциональна численности спортсменов, но при большем числе спортсменов не должна зависеть от их количества (
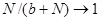при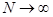 
). Скорость роста рекордов считается пропорциональной и их текущему значению 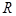. Общее количество рекордов в силу ограниченности физических возможностей человека не может быть больше некоторого предельного значения 
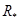. В третьем уравнении (3) это учитывается введением функции 
.
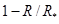Наличие рекордов у участников спортивной группы должно увеличить скорость роста индекса активности, но при этом их влияние должно быть ограниченным сверху. С другой стороны при их отсутствии скорость роста индекса активности не должна быть нулевой. Это учитывается во втором уравнении в (3) введением функции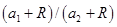 
с условием, что 
.
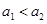Как и в модели (1) стационарная точка системы уравнений (3)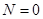 
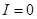будет неустойчивой. Во второй стационарной точке
, 
, 
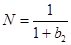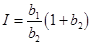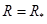
собственные значения матрицы Якоби правой части уравнений (3), удовлетворяющие уравнению
,
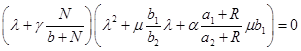будут иметь отрицательные вещественные части и, соответственно, эта стационарная точка будет устойчивой.
На рис. 7 для случая констант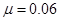 
, 
, 
, 
, 
, 
, 
, 
, 
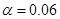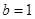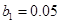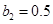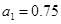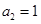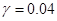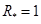показана зависимость 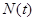(сплошная линия), а символом 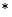отмечены статистические данные по числу спортсменов участников зимних Олимпийских игр с 1924 по 2014 гг. Число спортсменов участников олимпиады в 2014 года принято равным единице. Как следует из полученного результата за счет подбора констант в системе уравнений (3) можно получить решение, достаточно хорошо описывающее статистические данные.
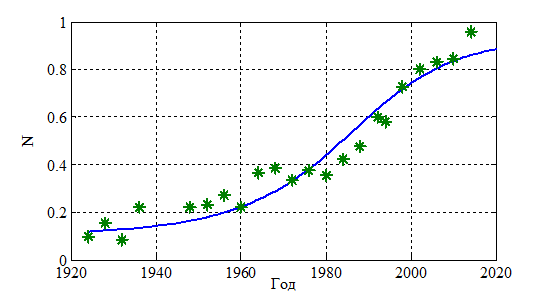
Рис. 7.
Заключение. Разработанные на основе статистических данных математические модели динамики спортивных сообществ позволяют объяснить изменение численности участников через «активность» общества. Недостаточное внимание к спортивным организациям и группам спортсменов, пренебрежение необходимостью обмениваться опытом, отсутствие популяризации знаний о роли спорта в жизни общества могут привести и к значительному уменьшению числа желающих заниматься спортом и участвовать в спортивных мероприятиях.
Литература:
1. Абдулина К. А., Старков В. Н. Квазистационарный подход в исследовании распространения насекомых в лесной системе // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 5-15.
2. Аленуров Э. А. Спортивная команда как малая группа. Часть 2 // Управление персоналом и интеллектуальными ресурсами в России. — 2014. — Т. 3. — № 3. — С. 65-69.
3. Алисов С. А., Гниломедов Р. А., Ефремов А. К. Активное формирование спортивной мотивации курсантов, занимающихся в группе совершенствования по волейболу // Вестник Воронежского института ФСИН России. — 2014. — № 2. — С. 69-72.
4. Ахапкин В. Н. Разработка приемных и переводных нормативов для спортсменов, обучающихся в группах начальной подготовки спортивных школ // Ученые записки университета им. П. Ф. Лесгафта. — 2013. — № 3 (97). — С. 14-19.
5. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
6. Болобан В. Н. Элементы теории и практики спортивной ориентации, отбора и комплектования групп в спортивной акробатике // Педагогика, психология и медико-биологические проблемы физического воспитания и спорта. — 2009. — № 2. — С. 21-32.
7. Буре А. В. Об одной теоретико-игровой модели тендера // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 25-32.
8. Буре В. М., Екимов А. В., Свиркин М. В. Имитационная модель формирования профиля мнений внутри коллектива // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 93-98.
9. Волков А. Н. Проблемы воспитания детей «группы риска» в системе детско- юношеских спортивных школ // Физическая культура: воспитание, образование, тренировка. — 2007. — – № 5. — С. 25-27.
10. Воронин С. М. Формирование у студентов мотивации к занятиям физической культурой и спортом // Вестник Ярославского государственного университета им. П. Г. Демидова. Серия Гуманитарные науки. — 2011. — № 1. — С. 34-36.
11. Гасратова Н. А., Бойцов Д. С., Крылова В. А., Гаврилова А. В. Модель Базыкина-Свирежева хищник-жертва // Молодой ученый. — 2014. — № 12 (71). — С. 8-12
12. Гасратова Н. А., Гасратов М. Г. Сетевая модель управления запасами для случая количественной конкуренции // Сибирский журнал индустриальной математики. — 2015. — Т. 18. № 1. — С. 14-27.
13. Гасратова Н. А., Столбовая М. В., Бойцов Д. С., Степанова Д. С. Математическая модель хищник-жертва на линейном ареале // Молодой ученый. — 2014. — № 11. — С. 1-10.
14. Грейвс Р. Мифы древней Греции. М.: Прогресс, 1992. — 624 с.
15. Грец И. А. Мотивация занятий спортом высококвалифицированных спортсменок и степень удовлетворенности жизненными планами после завершения спортивной карьеры // Ученые записки университета им. П. Ф. Лесгафта. — 2012. — № 2 (84). — С. 47-50.
16. Греция. М.: Мой мир, 2008. — 384 с. (Энциклопедия мировых цивилизаций).
17. Дергач Е. А., Завьялова О. Б. Мотивационный фактор как один из решающих в завершении спортивной карьеры спортсменов разных возрастных групп // Омский научный вестник. — 2013. — № 2 (116). — С. 228-231.
18. Дюк В. А., Кравчик М. Р., Сенкевич Ю. И. Обнаружение сублиминального визуального воздействия на человека средствами интеллектуального анализа данных электроэнцефалографических измерений // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 83-93.
19. Ежов П. Ф., Степанов А. В. Программа подготовки футболистов групп спортивного совершенствования на специальноподготовительном этапе // Теория и практика физической культуры. — 2012. — № 4. — С. 69.
20. Жук В. В., Тумка О. А. О некоторых модификациях обобщенной теоремы Джексона для наилучших приближений периодических функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 40-50.
21. Жук В. В., Тумка О. А., Козлов Н. А. О константах в неравенствах типа Джексона для наилучших приближений периодических дифференцируемых функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 33-41.
22. Ильинский С. В. Особенности мотивации спортсменов в различных видах спорта // Вестник Самарской гуманитарной академии. Серия: Психология. — 2013. — № 1. — С. 75-84.
23. Колабутин Н. В. Двухуровневая кооперация в дифференциальной игре технологического альянса // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2015. — № 1. — С. 42-63.
24. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. № 6 (96). — С. 226-232.
25. Колпак Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой ученый. — 2015. — № 3 (83). — С. 4-15.
26. Колпак Е. П., Габриелян Л А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6-14.
27. Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25-41.
28. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6-14.
29. Колпак Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12-22.
30. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20-30.
31. Колпак Е. П., Матвеева И. А. О библиотеках. Санкт-Петербург. 2004.
32. Колпак Е. П., Скороходова Т. В. Математическая модель роста числа учащихся в средней и высшей школах России. В сборнике: Синергетика в естественных науках. Восьмые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор: Лапина Г. П.. Тверь, 2012. — С. 274-275.
33. Кондручин А. Е. Стратегия развития спортивной организации с учетом формирования устойчивой мотивации к занятиям спортом // Педагогическое образование на Алтае. — 2014. — № 2. — С. 297-298.
34. Кун Л. Всеобщая история физической культуры и спорта. М.: Радуга, 1982. — 400 с.
35. Курникова М. В., Оринчук В. А., Фомичева Е. Н. Сценарий физкультурно-спортивного праздника для лиц с ограниченными возможностями различных нозологических групп // Физическая культура: воспитание, образование, тренировка. — 2013. — № 1. — С. 60-63.
36. Лебедев Д. М., Полякова Л. Н. Метод точных штрафов для решения одной задачи выпуклого программирования // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — № 1. — С. 72-78.
37. Лисейкина О. В. Регрессионные модели эффективности спортивной системы (на примере группы начальной подготовки отделения бокса детско-юношеской спортивной школы) // Образование. Наука. Инновации: Южное измерение. — 2012. — № 1 (21). — С. 58-63.
38. Литвинова А. В. Специальная физическая подготовка легкоатлетов группы спортивного совершенствования // Проблемы и перспективы развития образования в России. — 2013. — № 23. — С. 198-201.
39. Макаренко В. К. Формирование мотивации к занятиям физической культурой и спортом // Известия Пензенского государственного педагогического университета им. В. Г. Белинского. — 2008. — № 10. — С. 140-144.
40. Макина Л. Р. Исследование мотивации спортивной деятельности спортсменов с нарушением зрения учебно-тренировочных групп // Вестник Челябинского государственного педагогического университета. — 2011. — № 5. — С. 89-95.
41. Марченко В. Н., Нияскина А. В., Шилова В. Р. Тенденции развития олимпийского маркетинга // Молодой ученый. — 2014. — № 8. — С. 532-534.
42. Махов А. С. Информационно-потребностные компоненты формирования мотивации у инвалидов к занятиям адаптивным спортом // Вестник Балтийского федерального университета им. И. Канта. — 2010. — № 11. — С. 99-102.
43. Мельникова Н. Ю. Влияние игр XXIX олимпиады на формирование мотивации населения КНР к занятиям физической культурой и спорта // Спортивный психолог. — 2014. — № 3. — С. 89-92.
44. Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22-32.
45. Морозова Н. С. Виртуальные формации и виртуальные лидеры в задаче о движении строем группы роботов // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 135-149.
46. Олемской И. В., Фирюлина О. С. Алгоритм поиска наибольшего независимого множества // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 79-89.
47. Оркина Н. Б. Формирование мотивации к занятиям спортом у обучающихся через использование маркетинговых технологий // Проблемы развития физической культуры и спорта в новом тысячелетии. — 2014. — Т. 1. № 1. — С. 186-189.
48. Полякова Л. Н., Карелин В. В., Буре В. М., Хитров Г. М. Точные штрафные функции в задаче управления одной системой массового обслуживания // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 75-82.
49. Понявин А. В. Олимпийский маркетинг. М.: ЮНИТИ, 2005. — 127 с.
50. Провоторов В. В. Оптимальное управление параболической системой с распределенными параметрами на графе // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 154-163.
51. Пунин А. Л. Искусство древнего Египта: Среднее царство. Новое царство. СПб.: Азбука, 2010. — 656 с.
52. Репин В. А. Методические основы подбора стрелков-спортсменов в группу спортивного совершенствования // Вестник Волгоградской академии МВД России. — 2009. — № 4 (11). — С. 170-173.
53. Семенов В. А. Первобытное искусство: Каменный век. Бронзовый век. СПб.: Азбука-классика, 2008. — 592 с.
54. Слупко К. А. Периодические дифференциально-разностные системы. Алгоритм построения матрицы Ляпунова // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 150-159.
55. Созонтова Г. М. Развитие специальных физических качеств студентов, занимающихся настольным теннисом в группе спортивного совершенствования // Сборник научных трудов Ангарской государственной технической академии. — 2012. — Т. 1. № 1. — С. 176-182.
56. Талалай А. А. Занятия студентов в малых спортивных группах как фактор дальнейшей профессиональной успешности // Вестник Таганрогского государственного педагогического института. — 2008. — № 1. — С. 263-268.
57. Тихонов Г. Г., Семёнова Г. И., Яковых Ю. В. Специфика отбора спортсменов для формирования команд спортивного туризма в группе дисциплин «маршруты» // Омский научный вестник. — 2013. — № 1 (115). — С. 151-155.
58. Штоль Г. В. Мифы классической Греции. М.: Изд-ние Глазунова А.И.: 1876.
59. Щетинина С. Ю. Мотивация посещений уроков физической культуры и физкультурно-спортивной активности школьников разных половозрастных групп в зависимости от среды проживания // Физическая культура: воспитание, образование, тренировка. — 2009. — № 6. — С. 6-13.
60. Энциклопедия искусства Древнего мира. М.: Олма-Пресс Образование, 2002. — 352 с.
61. Якушев В. П., Карелин В. В., Буре В. М. Байесовский подход в задаче управления кислотностью среды // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 168-179.
