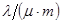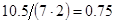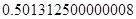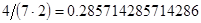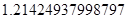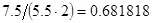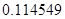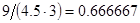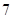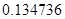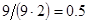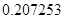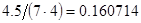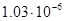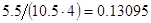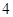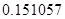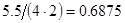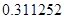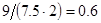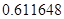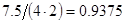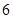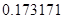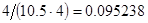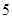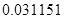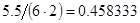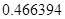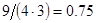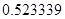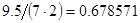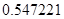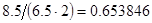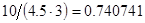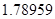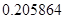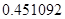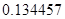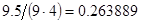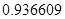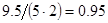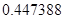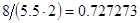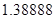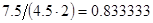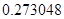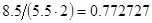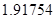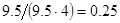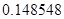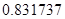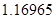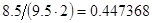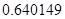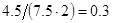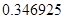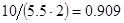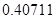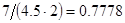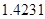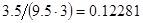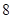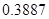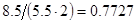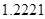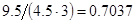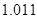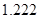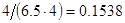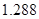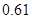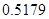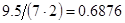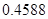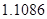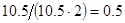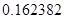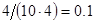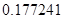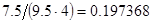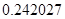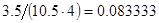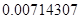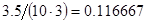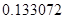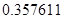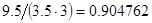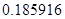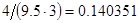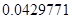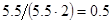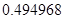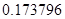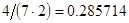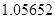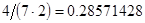Проверка численных моделей открытых СМО с ограничениями

Рассматривается численная модель открытой системы массового обслуживания, степень влияния соотношения входных параметров системы на погрешность вычисляемых динамических значений характеристик.

Ключевые слова:система массового обслуживания, характеристики системы, моделирование, проверка динамических значений

Первоначальная оценка погрешностей на этапе отладки алгоритма [3] производилась вручную путем создания нескольких прогонок (прогонкой здесь и далее называется запуск модели СМО от начала до достижения критерия остановки) модели одного типа и изменения входных параметров системы. Но больший интерес представляет дальнейшее исследование влияния входных параметров системы на динамические значения характеристик. Оценка погрешности и установление оптимальных входных параметров производились по нескольким критериям:

1.      Определение входных параметров, при которых максимальная погрешность определённой характеристики при некотором числе испытаний минимальна. Данную оценку можно применить к группам характеристик, объединенных общим признаком, например, число требований в системе, под обслуживанием и т. п.

2.      В некоторых случаях результат каждой из этих оценок необходимо проверить, вручную запустив прогонку модели с полученными входными параметрами и оценить поведение характеристик. Например, относительная погрешность величины, равная 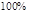, может говорить о том, что статическая величина, вычисляемая по формуле стремится к нулю, тогда как динамическая величина уже стала равной 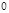, а относительная погрешность равная 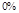, означает, что статическая величина чрезвычайно мала, что не позволяет хранить её значение в переменной, в результате чего, она также становится равной 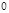. Однако такие случаи редки и довольно легко могут быть определены.

3.      Повторение испытания с увеличением максимального числа требований в системе, а также числа прогонок.

4.      Определение входных параметров, при которых максимальная погрешность испытаний по всем характеристикам созданной системы минимальна.

Погрешность испытаний также в значительной степени зависит от системы ГСЧ, используемой в созданной модели, поэтому этот параметр неизменен на протяжении всего испытания и выделен в отдельную характеристику при подсчёте погрешностей. По этой же причине, а также чтобы минимизировать влияние ГСЧ на результаты испытаний, оцениваться будут максимальные погрешности, а не средние или минимальные. Таким образом, оценка в целом будет заключаться в поиске такого сочетания входных параметров, при котором максимальная погрешность по всем испытаниям определенной характеристики будет минимальна. Поэтапная оценка алгоритма, моделирующего СМО открытого типа с очередью ограниченной длины [1], представлена ниже.

1.      Первым испытанием станет «поверхностная» проверка многоканальной СМО с неограниченной очередью с использованием встроенного псевдослучайного ГСЧ среды Visual Studio 2010 [2] и с ограничением максимального числа требований в системе равным 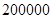. Цель — выявление наилучшего порядка величин  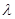и 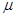. Также необходимо ограничить величину  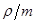интервалом 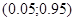, т. к. сходимость динамической системы в граничных условиях не может быть гарантирована. При указанных ограничениях и числе испытаний каждого соотношения равном 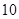, необходимо будет совершить  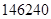прогонок. Наилучшим сочетанием входных параметров в целом, на основе определения минимальной погрешности наборов и максимальной погрешности характеристик в каждом наборе по всем прогонкам, для данного испытания является следующий набор, показанный в табл. 1.

Таблица 1

Наилучшее сочетание входных параметров в целом

Из-за различной скорости сходимости моментов разного порядка, данная оценка была разбита на 2 части.

2.      Последующая оценка погрешности СМО с очередью ограниченной длины производится аналогично, однако порядок величин 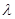 и 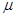 изменяться не будет. Ограничение максимальной длины очереди разумно ограничить слева 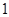, справа средней длиной реальной очереди модели без ограничений, умноженной на 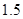. Список характеристик, наилучших сочетаний входных параметров и максимальных погрешностей данного испытания показаны в табл. 2, где в столбце «Огр». указано ограничение максимального числа требований в очереди.

Таблица 2

Сводная таблица испытания № 2

Примечание: из результатов исключена нулевая погрешность средней длины реальной очереди при ограничении максимальной длины очереди равно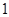й  или 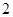, для исключения влияния этого вырожденного случая на оценку погрешности. На основании данных результатов можно сделать вывод, что сходимость моментов порядка выше 1 медленнее и требует увеличить число требований в системе.

3.      Основываясь на предыдущей оценке можно выбрать 5 наилучших сочетаний входных параметров для каждого момента порядка выше 1, что в результате даст 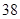 различных уникальных сочетаний, в виду повторения некоторых из них. Во втором испытании также будет использован встроенный псевдослучайный ГСЧ Visual Studio 2010, число прогонок для каждого набора увеличится до 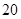, максимальное число требований же возрастет до 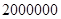, и оцениваться будут только моменты порядка выше 1. Список характеристик, наилучших сочетаний входных параметров и максимальных погрешностей данного испытания показаны в табл. 3.

Таблица 3

Сводная таблица испытания № 3

Наилучшие сочетания входных параметров в целом показаны в табл. 4.

Таблица 4

Наилучшее сочетание входных параметров в целом

Модель многоканальной СМО с отказами следует изучить отдельно.

Оценка погрешности данной системы производится аналогично, однако порядок величин 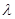 и 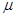 изменяться не будет, т. к. наилучший порядок уже был найден в испытании первой модели. Список характеристик, наилучших сочетаний входных параметров и максимальных погрешностей данного испытания показаны в табл. 5.

Таблица 5

Сводная таблица испытания № 4

Производить дальнейшие оценки данной модели, равно как и увеличивать максимальное число требований в системе, нет необходимости, динамические величины сходятся к значениям аналитических формул с приемлемой точностью. Наилучшие сочетания входных параметров в целом показаны в табл. 6.

Таблица 6

Наилучшее сочетание входных параметров в целом

Исследовано поведение модели [3] при различных наборах входных параметров, что позволило выявить наиболее удачные из этих сочетаний для созданных моделей СМО и отдельных характеристик, использование которых позволит снизить влияние ГСЧ на результаты прогонки. Результаты данного исследования будут полезны при поиске неизвестных пока аналитических формул характеристик СМО открытого типа с ограничениями.

Литература:

1.                  А. П. Кирпичников, Методы прикладной теории массового обслуживания. Казань, Изд-во Казанского университета, 2011. 200 с.

2.                  Microsoft Developer Network, Руководство по программированию на C#. https://msdn.microsoft.com/, 2014.

3.                  Шемахин Е. Ю., Кирпичников А. П. Моделирование многоканальных открытых систем массового обслуживания с ограничениями в среде Visual Studio 2010, Вестник Казанского технологического университета. 2015. Т.18, № 3.