В рамках модели лагов Алмон рассмотрено влияние инвестиций в основной капитал в Российской Федерации на уровень заработной платы. Выбиралась линейная и квадратичная структура лага. Приведены модельные соотношения и результаты их анализа в среде MATLAB.
Ключевые слова: лаг, метод наименьших квадратов (МНК), модель, прогнозирование, статистическая значимость, структура лага.
Существует множество объективных факторов, объясняющих эволюцию заработной платы в организации [1]. Нас интересовало, как влияют на этот важный показатель качества жизни населения инвестиции в основной капитал. В работе [2, с. 165] этот вопрос исследовался на базе данных за 1999 – 2011 г.г. В модели распределённых лагов Алмон было получено пригодное для прогнозов уравнение, описывающее связь указанных двух факторов. В работе предполагалась квадратичная структура лагов.
В настоящей работе расширен временной интервал анализа (1995 – 2012 г.г. [3]) и добавлены результаты исследований с линейной структурой лагов. Для анализа использовалась среда разработки MATLAB.
Исходную модель представим в виде
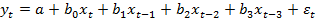. (1)
Стандартный МНК приводит к следующему результату
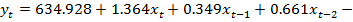
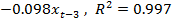(2)
Переходя к модели Алмон [4], рассмотрим две возможности.
1. Зависимость коэффициентов уравнения (1) от величины лага аппроксимируем полиномом первой степени
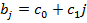, (3)
где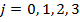 
.
Уравнение модели (1) принимает форму
,
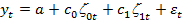где переменные Алмон имеют вид
,
,
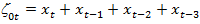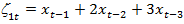а коэффициенты с0 и с1 подлежат оценке.
При таком подходе МНК даёт
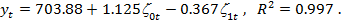
Уравнение в целом и каждый из трёх параметров статистически значимы.
2. Зависимость коэффициентов уравнения (1) от величины лага аппроксимируем полиномом второй степени
,
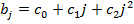где .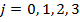
Уравнение модели (1) принимает форму
,
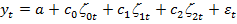с переменными
,
,
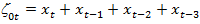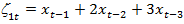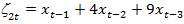
и коэффициентами с0, с1 и с2 , которые оцениваются МНК. Модельное уравнение
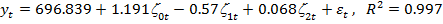
остаётся статистически значимым, однако, коэффициенты при переменных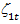 
и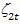 
– несущественны. Это служит основанием для предпочтения модели с линейной структурой лага.
Возвращаясь в ней к реальным переменным, получаем следующее уравнение
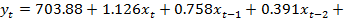
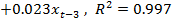(4).
Сравним уравнения (2) и (4). Оба уравнения существенны, но коэффициенты при переменных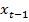 
, 
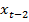и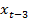 
в уравнении (2) статистически незначимы. Кроме того, коэффициент при 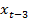в уравнении (2) – отрицателен, что бессмысленно с экономической точки зрения. Это позволяет говорить о неприменимости стандартного МНК к анализу выбранных данных.
Модель Алмон позволяет утверждать следующее. Рост инвестиций в основной капитал на 1 млрд. руб. приведёт через три года к увеличению среднемесячной заработной платы в РФ в среднем на 2.298 тыс. руб. Относительные коэффициенты регрессии составляют соответственно 0.49, 0.33, 0.17 и 0.01. Значительно более половины (82 %) воздействия фактора на результат осуществляется в первом году, причём 49 % всего воздействия – в текущем периоде.
Метод распределённых лагов даёт модельное уравнение, интерпретация которого выглядит адекватной. Уравнение (4) пригодно для перспективного прогнозирования.
Литература:
1. Выборнов В.И. Оценка финансового состояния организации / В.И. Выборнов, Н.В. Грищенко// Инновационные технологии в кооперативном образовании как фактор развития экономики: материалы международной научно-практической конференции в 7 ч. Белгород, 2009. С. 347-352.
2. Журавлёва Е.А. Алгоритм Алмон в исследовании динамики заработной платы в Российской Федерации / Е.А. Журавлева, В.И. Выборнов // Актуальные направления научных исследований XXI века: теория и практика: материалы международной заочной научно – практической конференции в 5 ч.: Ч.1. - Белгород, 2014. – С. 165 -167.
3. Российский статистический ежегодник. 2011: Стат. сб. – М.: Росстат, 2012.
4. Almon S. The distributed lag between capital appropriation and capital expenditures/ S. Almon // Econometrica. – Vol. 33. – 1965. – № 1 (January).
