Рассматривается разработка аддитивного обобщенного критерия качества на основе нормализованных безразмерных частных критериев, характеризующих отдельные свойства системы. Указываются приложения к оценке имитационных характеристик тренажеров транспортных систем, а также к синтезу композиционных материалов специального назначения.
Ключевые слова:сложные системы, оценка качества, критерии качества, обобщенный критерий качества, приложения.
На примере многокритериальной оценки имитационных характеристик транспортных тренажеров для подготовки операторов рассмотрим синтез аддитивного обобщенного критерия качества. В качестве частных критериев принимаются соответствующие параметры управляющих воздействий оператора в реальных и условиях тренажера.
Глобальный (обобщенный) критерий качества задается функционалом
,
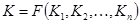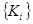— множество всех нормализованных безразмерных частных критериев
.
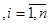Ограничимся функционалом в виде линейной функции
.
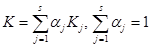Предполагается, что множество всех частных критериев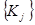 
разбито на 
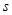групп. Каждая группа состоит из 
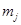критериев; 
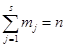. Критерии, входящие в 
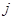-ую группу, обозначим 
, 
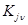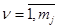. Использовались различные разбиения на группы. В частности, при разработке авиационных тренажеров разбиение на группы производилось по этапам полета (взлет, горизонтальный полет, посадка и т. д.; 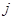- номер этапа). Использовалось и разбиение по качественным признакам (например, психологическая нагрузка пилота во время всего полета).
Уравнения регрессии для каждого из частных критерпев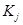 
представлялись в виде
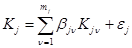, (1)
где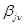 
— весовые константы; 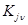- параметры оптимизации внутри 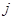-й группы, 
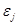— случайная ошибка (разница между действительным значением критерия 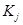и его значением по функционалу качества).
Определение весовых констант 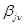— одна из наиболее важных задач многокритериального синтеза. Для ее решения использовался метод наименьших квадратов. Функция отклика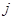-го критерия качества аппроксимировалась в виде (1). В каждой 
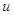-ой точке эксперимента
,
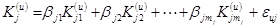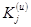— экспериментально полученное значение критерия в 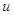-ой точке эксперимента, 
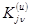- значения параметров оптимизации в этой точке.
Коэффициенты 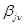выбирались из условия минимума суммы квадратов отклонений значений критерия качества, полученных экспериментально, от значений, предсказываемых уравнением регрессии:
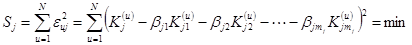. (2)
Точные значения 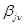могут быть определены лишь на основе бесконечного числа экспериментов (
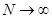), по всем возможным сочетаниям 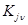и 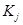. На практике число экспериментов всегда конечно. Поэтому можно говорить лишь об оценках 
= 
:
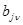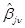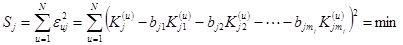. (3)
Оценки 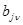весовых констант определялись из условия равенства нулю частных производных 
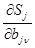. Каждое из слагаемых 
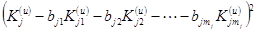обычно незначительно влияет на общую сумму (при большом N). При ограниченном числе опытов влияние слагаемых становится весьма заметным.
Для оценки веса каждого слагаемого в (3) введем коэффициенты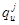 
. Тогда:
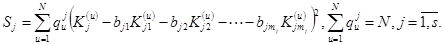(4)
В соответствии с (4) для определения оценок весовых констант получим систему нормальных уравнений
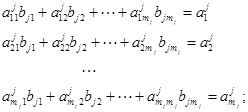(5)
, 
, 
.
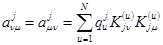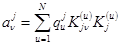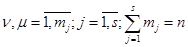Можно показать, при нормальном распределении справедливо
,
.
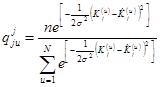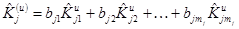Заметим, что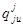 
есть функции от коэффициентов 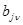. Так что система (5) может быть решена методом итераций:
, 
, 
;
; 
;
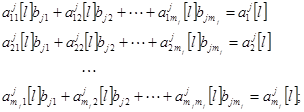
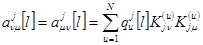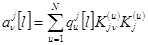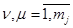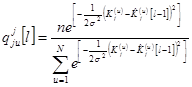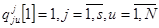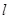- номер итераций.
При замене в последних формулах неизвестной дисперсии ее оценкой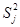 
будем иметь
.
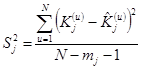Условие завершения итерационного процесса имеет вид:
,
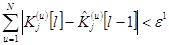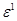— заданная малая величина.
Приведенный алгоритм эффективно использовался при синтезе обобщенного функционала качества для оценки имитационных характеристик авиационного тренажера по параметрам управляющих воздействий оператора на самолете и тренажере (оценка стиля управления) [1…5], а также при разработке композиционных материалов для защиты от радиации [6…8].
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник МАДИ. — 2011. –– № 2. — С.18–23
2. Гарькина И. А., Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. — 2013. -№ 1 (40). — С. 115–122.
3. Будылина Е. А.,Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3(17). — C. 150–156.
4. Гарькина И. А., Данилов А. М., Петренко В. О. Решение приближенных уравнений: декомпозиция пространственного движения управляемого объекта // Современные проблемы науки и образования. — 2014. — № 5; URL: www.science-education.ru/119–14766.
5. Будылина Е. А., Гарькина И. А., Данилов А. М., Пылайкин С. А. Аналитическое определение имитационных характеристик тренажных и обучающих комплексов // Фундаментальные исследования. — 2014. — № 6 (часть 4). — С. 698–702.
6. Гарькина И. А. Формализация оценки структуры и свойств композиционных материалов специального назначения / Строительные материалы. –2007. — № 1. — С.70–73.
7. Будылина Е. А., Гарькина И. А., Данилов А. М., Сорокин Д. С. Синтез композитов: логико-методологические модели // Современные проблемы науки и образования. — 2014. — № 5; URL:http://www.science-education.ru/119–14283
8. Пчелинцев И. А., Гарькина И. А. Итеративное формирование глобального критерия качества// Современные научные исследования и инновации. –2014. — № 12 [Электронный ресурс].URL: http://web.snauka.ru/issues/2014/12/41641
