В экспериментальной теплофизике различают две большие группы методов определения теплофизических свойств (ТФС) материалов: стационарные и нестационарные. Определение ТФС стационарным методом основано на том, что тепловой поток, проходящий через исследуемое тело во время проведения измерений, сохраняется постоянным по величине и направлению. Существующие стационарные методы отличаются друг от друга способами учета и компенсации потерь, формами и размерами исследуемых образцов, размещением нагревателей, конструкцией измерительных ячеек и зондов, приемами регистрации и обработки измерительной информации [1–3].
Следует отметить, что стационарные методы практически непригодны для определения ТФС материалов и изделий без нарушения их целостности. Серьезными недостатками стационарных методов являются большая длительность экспериментов, необходимость использования специально подготовленных образцов.
Методы определения ТФС материалов, основанные на закономерностях нестационарного потока тепла, можно разделить на методы регулярного режима и методы, основанные на определении параметров нестационарного температурного поля на начальной стадии его развития.
Различают регулярные режимы 1-го, 2-го и 3-го рода. Общая теория методов регулярного режима разработана Кондратьевым Г. М. и его учениками [3, 4].
Основными недостатками методов регулярного режима являются: длительность эксперимента; возможность проведения измерений только на специально подготовленных образцах определенной формы. Последнее затрудняет применение этих методов для неразрушающего контроля (НК) ТФС материалов.
Наиболее приемлемыми для НК ТФС материалов являются методы, основанные на определении параметров нестационарного температурного поля на начальной стадии процесса теплопроводности. В данных методах нестационарного теплообмена исследуемый образец моделируется в виде полуограниченного тела, что значительно уменьшает длительность эксперимента [5–7].
Отличительной чертой этих методов является то, что они не требуют изготовления образцов строго заданной формы и размеров, а подготовка к эксперименту заключается только в небольшой обработке ограниченного участка поверхности исследуемого образца, на который помещается измерительное устройство — зонд. С помощью зонда воздействуют тепловым потоком на исследуемое тело, снимают информацию о тепловом процессе и на ее основе по заданному алгоритму отыскивают значения ТФС.
Задачи по определению ТФС относятся к классу обратных задач моделирования [1]. Например, ТФС определяются на основе косвенных измерений — по температурному отклику образца на внешнее тепловое воздействие. Такие задачи, в общем случае, являются некорректно поставленными по Адамару и требуют, чтобы исследователи учитывали этот факт при построении математической модели процесса определения ТФС. В литературе в течение длительного времени была широко распространена точка зрения, что только корректно поставленные математические задачи могут описывать физические явления. Позже, помимо требований корректности по Адамару, было сформулировано понятие корректности по Тихонову. Подход А. Н. Тихонова позволил теоретически обоснованно решать обратные задачи, в том числе — обратные задачи теплопроводности.
Некорректность задачи по определению ТФС материалов будет определяться следующими факторами: непосредственно снимаемая экспериментальная информация (чаще всего температура) измеряется с определенной случайной погрешностью (DTсл); математическая модель, описывающая процессы, происходящие при измерении, является приближенной, вследствие чего при обработке экспериментально снятой информации возникают систематические погрешности (DTсист).
Рассмотрим, как эти два фактора проявляют себя при обработке экспериментальных данных. Будем считать, что в процессе эксперимента измеряется температура в фиксированные моменты времени и в заданной точке исследуемого образца [9, 10].
Тогда можем записать:
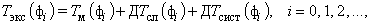(1)
где Tэкс — экспериментально снимаемая температура; Tм — модельная температура (ее вид известен из решения математической модели, положенной в основу метода измерения); DTсл — случайная составляющая погрешности измерения температуры; DTсист — систематическая погрешность, вызванная тем, что математическая модель приближенно описывает процессы, происходящие при измерении; ti — моменты времени, в которые измеряется температура.
Случайную погрешность DTсл можно рассматривать как случайную величину с нормальным или другим законом распределения. Ее конкретная величина зависит от используемых технических средств. Кроме того при исследовании композиционных материалов, представляющих собой сложные гетерогенные системы, к погрешности DTсл будет добавляться погрешность, связанная с различием локальных значений ТФС от их средних значений для данного материала [8, 11].
Погрешность DTсист будет в общем случае величиной, зависящей от времени и свойств материала, ее нельзя рассматривать как случайную величину.
Температура Tм представляет собой функцию времени, связывающую измеряемую температуру с геометрическими размерами, начальными и граничными (видом теплового воздействия) условиями, а также ТФС исследуемого материала. Как указывалось выше, вид функции Tм известен, то есть, можно записать
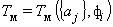, (2)
где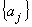 
— коэффициенты (параметры) модели, по которым определяются искомые ТФС (aj = f(ТФС материала)).
В свою очередь, для DTсист также можно записать
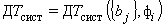, (3)
где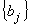 
– коэффициенты, зависящие от ТФС исследуемого образца и неучтенных факторов. В качестве этих факторов обычно выступают термические сопротивления, теплоемкости нагревателей и термоприемников и др. (bj = f(ТФС материала, неучтенные факторы)). Причем конкретный вид уравнения (2) обычно неизвестен.
Для обработки экспериментальных данных, с целью расчета ТФС, обычно используют два варианта.
По первому варианту, который применительно к неразрушающим контактным методам используется чаще всего, ТФС определяются на основе отдельных измерений температуры в заданные моменты времени. Например, если определяются два теплофизических свойства, то записывают два уравнения, соответствующих моментам времени tk1 и tk2:
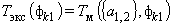, (4)
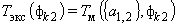. (5)
Так как Tэкс(tk1), Tэкс(tk2), tk1, tk2 известны, то решив систему (3) — (4), находят коэффициенты a1, a2, а по ним — искомые ТФС. Такой вариант решения обратной задачи имеет следующие недостатки. Во-первых, используется только малая часть полученной измерительной информации. Во-вторых, погрешность определения ТФС зависит от выбора tk1, tk2 и определяемых ТФС. Причем, ошибочный выбор tk1, tk2 может привести к тому, что Tм(tk) будет по величине сравнима с DTсист(tk) и погрешность определения ТФС будет неоправданно высокой. В-третьих, вследствие того, что ТФС определяются на основе отдельных измерений, значительное влияние на точность определения ТФС будет оказывать погрешность, связанная с неоднородностью исследуемого материала, что особенно важно для композиционных материалов [8].
По второму варианту ТФС определяются на основе всей снятой термограммы. В этом случае чаще всего используют следующий подход. Считают, что экспериментальные данные описываются уравнением (1) на всем временном интервале измерений. Затем, по методу наименьших квадратов проводится оценка параметров модели 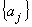. Здесь предполагается, что
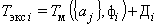, (6)
где Di — скрытая ошибка, имеющая известное распределение (обычно нормальное) с математическим ожиданием равным 0.
Кроме того, предполагается, что D не зависит от t. Однако, если сравнить (1) и (6), то можем видеть, что
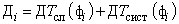. (7)
На самом деле D не является случайной величиной с математическим ожиданием равным нулю, и, кроме того, D зависит от t. Из теории математической статистики известно, что в этом случае оценки параметров модели 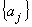будут смещенными и неэффективными. Практически, это означает, что при подобном «лобовом» подходе погрешность определения коэффициентов 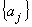может быть выше, чем при первом варианте обработки экспериментальных данных (определенные при таком подходе значения 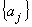могут не соответствовать их физическому смыслу, например, оказаться отрицательными, когда по своему физическому смыслу должны быть положительными). Кроме того, так как модель 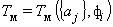в общем случае является нелинейной как по параметрам (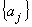), так и по независимой переменой (t), то значения 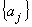будут также зависеть от начально заданного приближения (неустойчивость модели).
Вышесказанное особенно важно для контактных методов НК ТФС, так как здесь на ход эксперимента оказывают влияние куда больше факторов, чем в случае, если ТФС определяются при помощи стационарной установки на специально подготовленных образцах. И даже, если удается получить вид зависимости 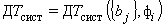, то для ее вычисления требуется информация, которая или заранее неизвестна (например, термические сопротивления), или трудноопределима (например, теплоемкость нагревателя) [8].
Часто, для уменьшения влияния DTсист используют, так называемую, модель введения поправок. Такой подход имеет следующие недостатки. Во-первых, не решается вопрос о более полном использовании информации, полученной в результате эксперимента (т. к. используются отдельные точки термограммы). Во-вторых, остается нерешенным вопрос о выборе моментов времени, в которые необходимо проводить измерения. В-третьих, так как модель введения поправок базируется на эмпирической формуле, то для расчета ее параметров необходимо иметь достаточное количество образцов с известными ТФС. Причем диапазон достоверного определения ТФС по этой модели будет определяться имеющимися образцами с известными ТФС.
Анализ литературных данных показал, что наиболее точно учитываются как систематические, так и случайные погрешности в методах, основанных на регулярном тепловом режиме [3, 4]. А. В. Лыковым было показано [1], что регулярные тепловые режимы первого и второго рода имеют общее свойство, которое характеризуется независимостью от времени отношения теплового потока q в любой точке тела к потоку тепла на его поверхности qп. В частном случае, когда на поверхности образца действует источник тепла постоянной мощности, в теле возникает стационарное поле тепловых потоков.
Характерной особенностью методов измерения ТФС, основанных на регулярном тепловом режиме, является простота расчетных формул. Математическая модель, описывающая термограмму, чаще всего является линейной по параметрам или легко линеаризуется. Систематические погрешности учитываются в виде независимых от времени и простых по форме поправок. Однако основная часть этих методов базируется на моделях для тел конечных размеров (пластина, цилиндр, шар). В то время как большая часть методов НК базируются на моделях полупространства (плоского, цилиндрического, сферического). Можно показать, что вышеприведенное высказывание А. В. Лыкова применимо и для таких моделей. Однако, в этом случае нужно говорить не о регулярном тепловом режиме для всего тела в целом (т. к. оно принимается неограниченным), а о регуляризации теплового процесса только для какой-то определенной области тела. В этом случае, ход термограммы будет определяться, прежде всего, внутренними слоями исследуемого образца. Основными источниками систематических погрешностей в контактных неразрушающих методах контроля ТФС являются неучтенные процессы в области нагревателя и теплоприемников (термические сопротивления, теплоемкости и др.).
Отсюда можно сделать вывод, что, если проводить измерение ТФС основываясь только на участках термограммы, соответствующих регуляризации теплового режима в области нагревателей и термоприемников, то, во-первых, расчетные соотношения будут простыми и во многих случаях линейными по параметрам; во-вторых, систематические погрешности будут либо значительно меньшими, чем случайные, либо будут носить постоянный характер, т. е. не будут зависеть от времени (DTсист=const).
Литература:
1. Лыков, А. В. Теория теплопроводности / А. В. Лыков. — М.: Высшая школа, 1967. — 599 с.
2. Платунов, Е. С. Теплофизические измерения и приборы / Е. С. Платунов, С. Е. Буравой, В. В. Курепин, Г. С. Петров. — Л.: Машиностроение, 1986. — 256 с.
3. Кондратьев, Г. М. Регулярный тепловой режим. — М.: Гостехиздат, 1954. — 408 с.
4. Кондратьев, Г. М. Тепловые измерения. — М. — Л.: Машгиз, 1956. — 253 с.
5. Жуков, Н. П. Моделирование процесса теплопереноса от плоского источника тепла постоянной мощности при теплофизических измерениях / Н. П. Жуков, Н. Ф. Майникова // Инженерно-физический журнал. — 2005. — Т. 78, № 6. — С. 56–63.
6. Майникова, Н. Ф. Измерительно-вычислительная система неразрушающего теплофизического контроля / Н. Ф. Майникова, Н. П. Жуков // Приборы и техника эксперимента. — 2005. — № 2. — С. 153–154.
7. Жуков, Н. П. Измерительно-вычислительная система неразрушающего контроля теплофизических свойств / Н. П. Жуков, Н. Ф. Майникова // Приборы и техника эксперимента. — 2005. — № 3. — С. 164–166.
8. Майникова, Н. Ф. Об одном методе термического анализа для неразрушающего контроля теплофизических свойств полимеров / Н. Ф. Майникова, И. В. Рогов, А. А. Балашов // Пластические массы. - 2001. - № 2. - С. 30 - 33.
9. Жуков, Н. П. Моделирование процесса теплопереноса от плоского источника тепла при теплофизических измерениях / Н. П. Жуков, Ю. Л. Муромцев, Н. Ф. Майникова // Вестник Тамбовского государственного технического университета. — 1999. — Т. 5, № 4. — С. 543–553.
10. Майникова, Н. Ф. Исследование теплофизических свойств композитов строительного назначения / Н. Ф. Майникова, И. В. Рогов, З. М. Селиванова // Вестник Тамбовского государственного технического университета. — 1999. — Т. 5, № 2. — С. 285–289.
11. Жуков, Н. П. Анализ погрешностей метода измерения теплофизических характеристик композитов. Оценка случайных погрешностей / Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов // Вестник Тамбовского государственного технического университета. — 2000. — Т. 6, № 3. — С. 416–424.
