В данной статье нам хотелось бы рассмотреть примерное содержание блоков при использовании технологии модульного обучения в математике. Динамичная структура модуля позволяет представить каждую тему, а в целом и содержание курса математики в трех различных вариантах: полном, сокращенном и углубленном. Причем выбор того или иного варианта осуществляется самим учащимся после прохождения входного актуализирующего контроля и реальной оценки своих познавательных возможностей. Как правило, полный вариант модуля рекомендуется для слабых учащихся, сокращенный вариант — для средних и углубленный — для сильных учащихся. Поэтому вариативность модуля проявляется при дифференциации учебного материала с учетом потребностей профессиональной подготовки учащихся.
Модификация общей структуры модуля, предложенная М. А. Чошановым, применительно к обучению высшей математики приведена на схеме. Рис1.
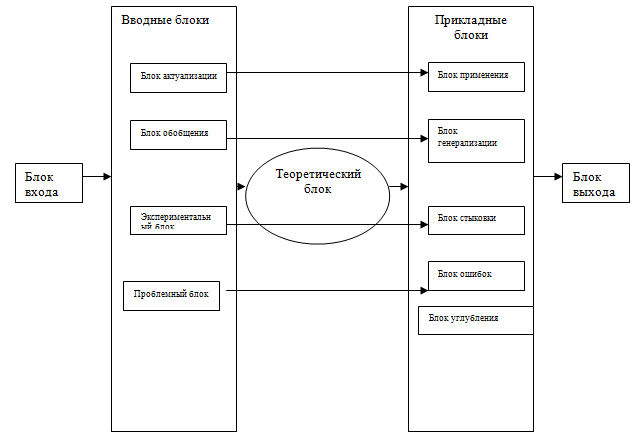
Рис. 1. Общая структура модуля.
Таким образом, каждый модуль имеет структуру, отражающую основные элементы: входной уровень; планируемые результаты обучения (знания, умения, навыки); содержание (учебный материал, методы и формы обучения); процедуры оценки. Преимущество работы с модулем выражается не только в свободе выбора студентом индивидуального темпа обучения, возможности организации полной самостоятельной деятельности, но и в вариативности в выборе содержания лекционных и практических занятий по математике, с учетом логики самого предмета и специфики специальности студентов.
Рассмотрим на примере темы «Числовые ряды» содержание каждого из блоков представленных в таблице.
Блок актуализации. Содержит тестовые задания предполагаемые актуализацию тех опорных знаний и способов действий, которые необходимы для усвоения содержания всего модуля; следует включить следующие темы: последовательность, бесконечно большие и бесконечно малые величины, сумма последовательности, признаки существования предела последовательности, предел последовательности, первый и второй замечательные пределы, арифметическая и геометрическая прогрессии.
Проблемный блок. Всегда ли последовательность имеет предел, нахождение предела частичных сумм.
Экспериментальный блок: провести лабораторную работу по двум вариантам, вывод которой будет следующим: бесконечная геометрическая прогрессия представляет ряд, который сходится при |q| < 1 и расходится при |q| ³ 1.
Блок обобщения. Наглядно представить схему всех признаков сходимости ряда. Это можно в виде «дерева» где, исходя из вида ряда, проверить необходимый признак сходимости, а затем воспользовавшись одним из признаков сходимости сделать вывод о поведении ряда. Рис 2.
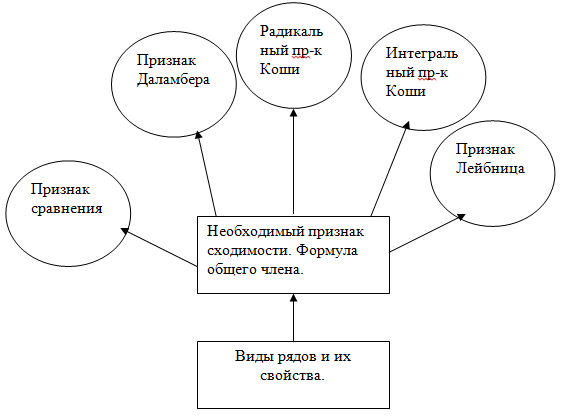
Рис. 2 «Дерево» признаков сходимости
Теоретический блок. Содержит изучение следующих понятий: определение ряда, сумма ряда. Сходимость. Гармонический ряд. Необходимый признак сходимости ряда. Ряды с положительными членами. Достаточные признаки сходимости (признак сравнения, Даламбера, интегральный признак Коши, радикальный признак). Знакочередующиеся ряды. Теорема Лейбница. Знакопеременные ряды. Абсолютная и условная сходимость. Свойства абсолютно сходящихся рядов.
Блок ошибок. Отработать ошибки по применению критериев сходимости ряда, ошибки по определению вида ряда, а также о правильном выводе по решению.
Блок применения. Решение задач на установление сходимости ряда, на применение признаков сходимости, на абсолютную и условную сходимость, т. е. на все пункты изученные в теоретическом блоке.
Блок углубления. Ряды с комплексными членами, условия их сходимости.
Блок стыковки. Решение задач из экспериментального блока на геометрическую прогрессию через известные признаки сходимости ряда.
Блок выхода. Содержит аудиторную контрольную работу по изученной теме.
Практика применения модуля показывает, что для слабых учащихся целесообразно рекомендовать полный вариант, который содержит блоки, входящие в инвариантную структуру, а также следующие блоки: актуализации, экспериментальный, применения и блок ошибок, которые расширяют эмпирическую базу учебной информации, направленную на обеспечение доступности содержания модуля. Сокращенный вариант содержит блоки инвариантной структуры, а также проблемный блок и блок стыковки и соответствует более высокому уровню обобщения, поэтому его рекомендуют средним учащимся. Углубленный вариант отличается от сокращенного наличием блока углубления и рекомендуется для наиболее подготовленных, сильных учащихся.
Литература:
1. Акимова И. В., Губанова О. М., Титова Е. И. Возможности реализации модульного подхода при обучении бакалавров педагогических специальностей на примере темы «Введение в алгебру логики»// Современные проблемы науки и образования. № 5.-2013 г.
2. Ермолаева Е. И. Особенности реализации модульного обучения в системе высшего образования //В мире научных открытий. 2010. № 4–5. С. 109–110.
3. Ермолаева Е. И. Проблемы усвоения математических знаний студентами технических вузов //Актуальные проблемы гуманитарных и естественных наук. 2010. № 7. С. 270–272.
4. Жидкова А. Е., Титова Е. И. Рекомендации для преподавателей по использованию технологии модульного обучения// Молодой ученый. 2014. № 2 (61). С. 756–757.
5. Родионов М. А., Макаров Ю. А. Психология мотивации учебной деятельности: Учебное пособие. — Пенза: ПГПУ, 2004г
6. Чошанов М. А. Гибкая технология проблемно-модульного обучения. — М.: Народное образование, 1996г.







