Современное развитие науки характеризуется потребностью сложного изучения всевозможных сложных процессов и явлений — физических, химических, биологических, экономических, социальных и других. Происходит значительное увеличение темпов математизации и расширение ее области действия. Применение математического моделирование настолько широко и применяется в других науках, казалось бы совершенно далеких от математики — лингвистике, юриспруденции и рассмотренной нами в данной статье биологии.
Задача, как правило, порождена потребностями той или иной прикладной области и математически моделирую ее мы получаем решение различных вопросов, казалось и не связанных с математикой. Вполне понятно, что при этом происходит одна из возможных математических формализаций реальной ситуации. Рассмотрим одну из задач биологии. Число особей в популяции меняется со временем. Если условия существования популяции благоприятны, то рождаемость превышает смертность и общее число особей в популяции растет со временем. Опишем математически данную задачу. Назовем скорость роста популяции прирост числа особей в единицу времени. Обозначим эту скорость v=v(t). В «старых», установившихся популяциях, давно обитающих в данной местности, скорость роста v(t) мала и медленно стремится к 0. Но если популяция молода, ее взаимоотношения с другими местными популяциями еще не установились или существуют внешние причины, изменяющие эти взаимоотношения, например сознательное вмешательство человека, то v(t) может значительно колебаться, уменьшаться или увеличиваться.
Если известна скорость роста популяции v(t), то мы можем найти прирост численности популяции за промежуток времени от t0 до Т. В самом деле из определения v(t) следует, что эта функция является производной от численности популяции N(t) в момент t, и, следовательно, численность популяции N(t) является первообразной для v(t). Поэтому
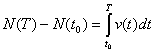(1)
Известно, что в условиях неограниченных ресурсов питания, скорость роста многих популяций экспоненциальна, т. е. v(t) = aekt. Популяция в этом случае как бы «не стареет». Такие условия можно создать, например, для микроорганизмов, пересаживая время от времени развивающуюся культуру в новую емкость с питательной средой. Применяя формулу (1), в этом случае получим:
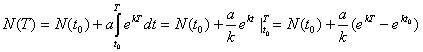(2).
По формуле, подобной (2), подсчитывают, в частности численность культивируемых грибков, выделяющих пенициллин.
Рассмотрим микробиологическую задачу. Установим закон изменения со временем (t) численности бактерий (N), помещенных в питательную среду.
Для составления дифференциального уравнения, отражающего существование бактерий в этих условиях, необходим некоторый факт, который следует записать в математической форме. На основании экспериментальных данных и общих соображений таким фактом может служить утверждение: “скорость размножения бактерий (математически) пропорциональна их числу (N) в данный момент времени”.
Таким образом, необходимое дифференциальное уравнение имеет вид:
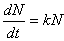(3)
где k — доступный экспериментальному определению коэффициент пропорциональности, зависящий от вида бактерий и параметров среды их обитания. Дополнительные данные, необходимые для решения задачи следуют из начального условия: при t=0, N=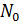
, т. е. в начальный момент времени количество бактерий считается известным и равным .
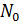Для решения уравнения (3) произведем разделение переменных и последующее интегрирование:
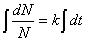
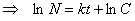(4)
Произвольную постоянную в уравнении (4) удобно представить в виде lnС. Из начального условия: C=.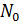
Решая логарифмическое уравнение (4) с учетом начального условия, получим искомый закон изменения числа бактерий со временем:
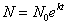. (5)
Произведем некоторый анализ результата. В чем его сиюминутная практическая полезность и возможные более отдаленные выводы?
1) Зная коэффициент k и начальное число бактерий 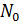, легко определить их число в любой момент времени t.
2) Прирост бактериальной массы определяется через коэффициент k условиями среды обитания бактерий. Чем больше значение k, тем быстрее увеличивается число бактерий
Если существуют факторы, препятствующие размножению бактерий (повышенная температура, ионизирующие излучения и др.), то коэффициент k в формулах (4) — (5) уменьшается и может принять отрицательное значение — в этом случае будет наблюдаться гибель бактерий.
3) С некоторым риском можно попытаться придать полученному для бактерий результату (5) большую общность и сформулировать утверждение: «любой биологический вид, находясь в оптимальных для своего существования условиях, экспоненциально увеличивает свою численность со временем». Примеры справедливости этого утверждения можно наблюдать. Так, кролики, завезенные в Австралию, где практически нет хищников, которые бы ими питались, увеличили свое число в соответствии с формулой (5) и стали представлять серьезную опасность для сельского хозяйства.
Рассмотрим пример решения данного типа задач: Выращена популяция бактерий численностью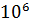 
. Внезапно начинается гибель бактерий, причем за первую минуту число погибших бактерий составило
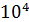.Определить, за какое время погибнет вся популяция, если известно, что скорость гибели пропорциональна численности популяции.
Изменение численности популяции N запишем дифференциальным уравнением
; 
;
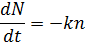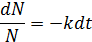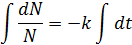; lnN=-kt+lnC
N=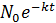
; C=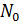
Найдем k: K=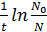
По условию за 1 минуту погибло 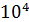бактерий, значит K=0,01
Время гибели t=
ln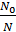
Считая нижней границей популяции значение N = 1, окончательно получаем
t=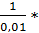
ln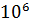=100*ln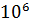=600*ln10≈1382минуты≈23часа
Получили решение биологической задачи путем составления математической модели и применения интегрального исчисления.
Литература:
1. Акимова И. В., Ермолаева Е. И. Использование специальных программных средств в математическом моделировании// В мире научных открытий. 2012. № 5.4. С. 85–96.
2. Ермолаева Е. И. Математическое моделирование физических процессов в теории вероятностей// Актуальные проблемы гуманитарных и естественных наук. 2010. № 10. С. 13–15.
3. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах// Молодой ученый. 2013. № 12 (59). С. 3–6.
