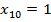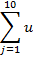1. Постановка задачи и предворительного результаты:
Пусть, функция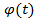 -возрастающая и непрерывная функция на G, где G= [a,b].
-возрастающая и непрерывная функция на G, где G= [a,b].
Рассмотрим интегрального уравнение
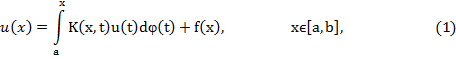
где К(x,t)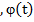 и f(x) –известные функции, u(x)-искомая функция.
и f(x) –известные функции, u(x)-искомая функция.
(1)-называется линейным интегральным уравнением Вольтерра-Стильтьеса второго рода.
В общем случае, уравнение (1) не сводятся к интегральным уравнениям Вольтерра, так как интеграл Стильтеса не всегда сводится к интегралу Римана или интегралу Лебега. [5]. Различные приближенные методы решения линейных интегральных уравнений Вольтерра первого рода изучены в многих работах [1].
2. Применение обобщенной формулы трапеции для интеграла Стильтьеса:
Рассмотрим обобщенную формулы трапеции для интеграла Стильтьеса [6], [7]
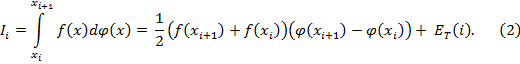
где h=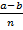 , n
, n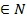 ,
, 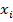 =a+ih, i=0,1,2,3,…,n, a
=a+ih, i=0,1,2,3,…,n, a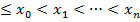
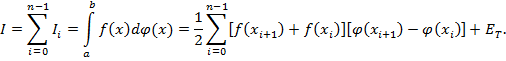
Здесь
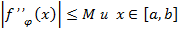 тогда, остаток оценивается
тогда, остаток оценивается
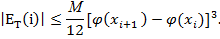
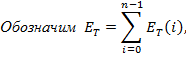
тогда, получаем
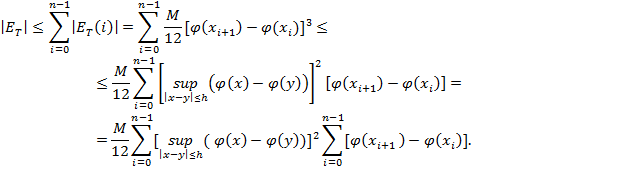
Здесь
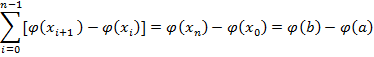
Далее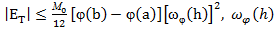 =
=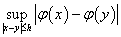

3. Применение обобщенной формулы трапеции для интегрального уравнении Вольтерра-Стильтеса:
Рассматривается (1) уравнение
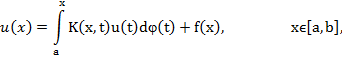
где h=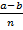 , n
, n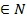 ,
, 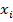 =a+ih, i=0,1,2,3,…,n,
=a+ih, i=0,1,2,3,…,n,
применяя формулу (2) получим
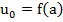 ,
, 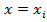 , (i=1,2,3,…,n),
, (i=1,2,3,…,n),
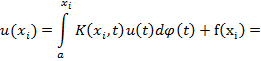
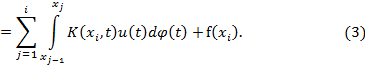
Теперь, применяя формулу (2)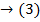 получаем
получаем
u(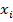 )=
)=
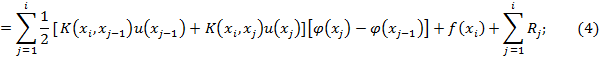
где ⃓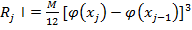 , здесь
, здесь 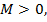
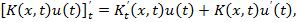
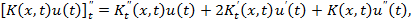

Пусть 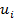 является решением следующей системы
является решением следующей системы
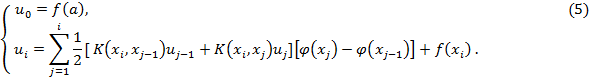
Учитывая (4) и (5) имеем
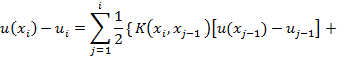
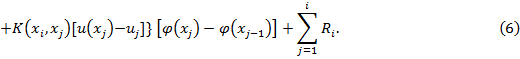
Введя новую функцию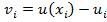 получим
получим
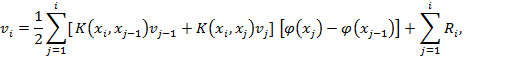
оценим остаток
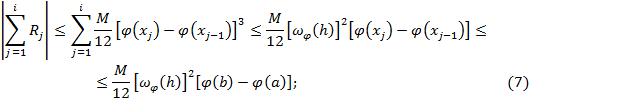
где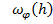 =
=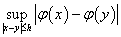
Полагаем что, 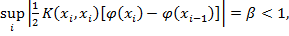
Далее, из (5) имеем
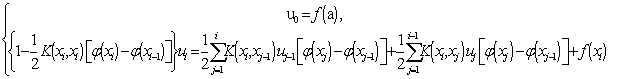
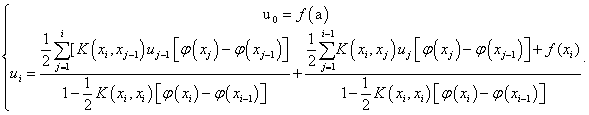 (8)
(8)
Таким образом (8) является алгоритм приближенное решения интегральных уравнения (1).
4. Пример: Рассмотрим уравнение
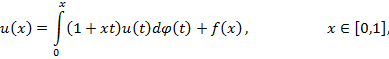
Здесь [x,t]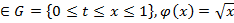 ,
, 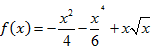
Решение: Вычислим по обобщенной формуле трапеций при n=10. Имеем
h=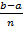 =
=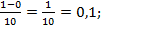 i=0,1,2,3,4,5,6,7,8,9,10;
i=0,1,2,3,4,5,6,7,8,9,10; 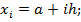
Применяя формула (8) с помощью микрокалькулятора получаем следующие значение
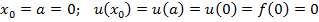 ;
; 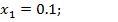
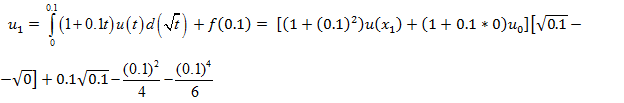 ;
;
u(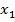 )=
)=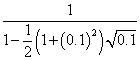
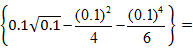 0.0367;
0.0367;
Точное решение данного интегрального уравнения является
u(x)=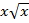 ,
, 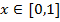 потому что, нетрудно догадаться, что
потому что, нетрудно догадаться, что

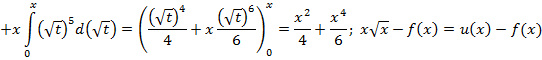
Сравнивая точное решение и приближенное решение, найдем погрешность данного интегрального уравнения. (Таблица 1)
Таблица 1
|
|
|
u( |
|
|
|
0,0367 |
0,0316 |
0,0051 |
|
|
0,0939 |
0,0894 |
0,0045 |
|
|
0,1698 |
0,1643 |
0,0055 |
|
|
0,2593 |
0,2530 |
0,0063 |
|
|
0,3609 |
0,3535 |
0,0074 |
|
|
0,4733 |
0,4647 |
0,0086 |
|
|
0,6411 |
0,5857 |
0,0118 |
|
|
0,7314 |
0,7155 |
0,0159 |
|
|
0,8721 |
0,8538 |
0,0183 |
|
|
1,0212 |
1 |
0,0212 |
|
|
4,6597 |
4,5117 |
0,148 |
Погрешность составляет 0,148.
Еще с помощью программу Delpi точнее результат выводим.
Код программы и график:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids, TeEngine, Series, ExtCtrls, TeeProcs, Chart;
type
TForm1 = class(TForm)
lbl1: TLabel;
lbl2: TLabel;
edt1: TEdit;
edt2: TEdit;
lbl3: TLabel;
edt3: TEdit;
strngrd1: TStringGrid;
btn1: TButton;
cht1: TChart;
btn2: TButton;
lnsrsSeries1: TLineSeries;
lnsrsSeries2: TLineSeries;
procedure btn1Click(Sender: TObject);
procedure btn2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
n:Integer;
u,x:array[0..1000] of Real;
implementation
{$R *.dfm}
function f(x:Real):Real;
begin
f:=x*sqrt(x)-sqr(x)/4-sqr(x)*sqr(x)/6;
end;
function fi(x:Real):Real;
begin
fi:=sqrt(x);
end;
function k(x,t:Real):Real;
begin
k:=1+x*t;
end;
//tochnoe reshenie, esli izvestno
function uu(x:Real):Real;
begin
uu:=x*sqrt(x);
end;
procedure TForm1.btn1Click(Sender: TObject);
var
a,b,h,c,s:Real;
i,j:Integer;
begin
// vvod dannyh
a:=StrToFloat(edt1.Text);
b:=StrToFloat(edt2.Text);
n:=StrToInt(edt3.Text);
//predvoritelnye raschety
h:=(b-a)/n;
x[0]:=a;
for i:=1 to n do x[i]:=x[i-1]+h;
// regulirovka strok
strngrd1.RowCount:=n+2;
strngrd1.Cells[0,0]:='x';
strngrd1.Cells[1,0]:='u';
for i:=0 to n do strngrd1.Cells[0,i+1]:=FloatToStrF(x[i],ffFixed,8,5);
//vychisleniya
u[0]:=f(x[0]);
for i:=1 to n do begin
j:=1;
c:=f(x[i])+(fi(x[i])-fi(x[i-1]))*k(x[i],x[i-1])*u[i-1]/2;
s:=1-k(x[i],x[i])*(fi(x[i])-fi(x[i-1]))/2;
while j<i do
begin
c:=c+(k(x[i],x[j-1])*u[j-1]+k(x[i],x[j])*u[j])*(fi(x[j])-fi(x[j-1]))/2;
j:=j+1;
end;
u[i]:=c/s;
end;
//Vyvod
for i:=0 to n do strngrd1.Cells[1,i+1]:=FloatToStrF(u[i],ffFixed,8,5);
btn2.Visible:=True;
end;
procedure TForm1.btn2Click(Sender: TObject);
var
i:Integer;
begin
//ochishenie
cht1.SeriesList[0].Clear;
cht1.SeriesList[1].Clear;
//grafik
for i:=0 to n do
begin
cht1.SeriesList[0].AddXY(x[i], u[i],' ', clRed);
cht1.SeriesList[1].AddXY(x[i], uu(x[i]),' ', clGreen);
end;
end;
end.
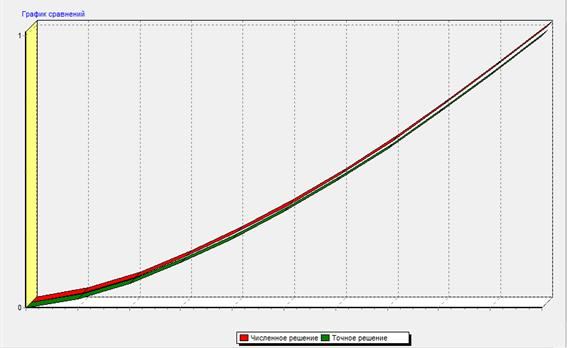
График
Литература:
1. А. В. Манжиров, А. Д. Полянин «Справочник по интегральным уравнением, методы решения», Москва, 2000г.
2. A.Асанов. (2000) Производная функции по возрастающей функции. Fen Bilimleri DERĜİSİ, Кыргызко-Турецкий Университет «Maнас», № 1,с 18–64.
3. С. Г. Михлин. Лекции по интегральным уравнениям. Москва, 1956.
4. Г. М. Мюнтц. Интегральные уравнения. Москва, 1934.
5. И. П. Натансон. «Теория функций вещественный переменной», Наука, Москва, 1974.
6. Avyt Asanov, Haluk Chelik, Ali Chalish. APPROXIMATING THE STIELTJES INTEGRAL BY USING THE GENERALIZED TRAPEZOID RULE. LE MATEMATICHE, c 13–21, 2011.
7. Ali Çalış, Stiltjes integralinde sayısal yaklaşım metodları, Bişkek, 2010.







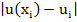
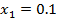
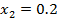
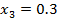
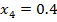
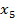 =0.5
=0.5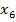 =0.6
=0.6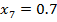
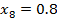
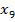 =0.9
=0.9