Применение теоремы Паппа-Гульдена

Методика нахождения объемов и плошадь поверхности разнообразны, следует отметит следующие основные методы.

1)   Объемы тел вращения определяются как пределы последовательностей объемов вписанных и описанных многогранников, при этом сложность составляет вычисление объёма шара, приходится выводить формулу для объема тела вращения через определенный интеграл.

2)   Вычисление объёмов тел с помощью определенного интеграла.

3)   С помощью принципа Кавальери, который принимается за дополнительную аксиому объёмов.

4)   По формуле Симпсона.

Разработана методика изучения темы в условиях профильной школы.

1)        Применение принципа Кавальери для нахождения объема шара и его частей, объема “арбузной дольки”, “шарового кольца”, “копыта” (через центр основания прямого кругового цилиндра под острым углом к плоскости основания проходит плоскости).

2)        Применение теоремы Гульдена-Паппа для нахождения объемов тел, возникающих при вращении треугольника, трапеции, полукруга, круга, четверти круга, сегмента круга (объем тела вращения фигура, лежащей в плоскости целиком по одну строну от оси вращения, равен произведению площади фигуры и длины окружности, которую описывает центр масс фигуры при вращении:

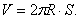
3)        Эквивалентные замены, при нахождение объема тела вращения (фигура вращения, оси).

В качестве собственного открытия Папп формулирует теорему относительно объемов тел вращения, которая, в сущности, есть не что иное, как известная теперь «теорема Паппа-Гульдена». Там же содержаться комментарии к работам Аполлония Пергского, в частности к его «коническим сечениям». Много работ посвящена, в большей своей части механике, но содержит, кроме того, и построение конического сечения, проходящего через пять данных точек. Поводом для этого послужила задача: определить диаметр цилиндрической колонны по произвольному ее обломку. Папп написал ряд других трудов, в частности трактат «Хронография математики», в котором положил начало алгебраическим знаком, что было немаловажным достижением, если учитывать те трудности, которые возникали при письменной передачи математических достижений. К сожалению труди эти были безвозвратно утеряны. Многие леммы Паппа содержат, идеи уже настоящей проективной геометрии. И когда спустя много веков люди это осознали, Папп был назван последним великим геометром древности. Но помимо достижений в геометрии Папп достиг достаточно высокого уровня и в разработке практического применения интегрального исчисления. Один из важнейших теорем высшей математики были сформулированы им а через много веков над ними работал Гульден. Теперь они известны как 1-я и 2-я теоремы Паппа-Гульдена. 1-я теорема Паппа-Гульдена Ордината центра тяжести дуги плоской кривой: Площадь поверхности тела вращения равно произведению длины окружности, описываемой центром тяжести, на длину этой кривой 2-я теорема Паппа-Гульдена: Объем тела вращения равен произведению длины окружности, описываемой центром тяжести фигуры на ее площадь. Эти теоремы используется в инженерной практике, особенно, если кривая или фигура сложной формы. Таким образом, в XVII веке началась эпоха интегрального исчисления. Математики возвращались к задачам о вычислении площадей криволинейных фигур и объемов «кривых» тел, которыми так успешно занимался в древности Архимед.

Интересовался этим вопросом и итальянский монах Б.Кавальери. В переписке с Г.Галилеем они обсуждали разнообразные механические и математические проблема, и в частности метод «неделимых». В 1635 г вышла книга Кавальери «Геометрия, изложенная новым способом при помощи неделимых гостей непрерывных величин».

При вычислении площадей многоугольников бывает полезно преобразовать фигуры, не меняя их площадей. Например разрезать на части и составлять новые. Так можно преобразовать друг в друга треугольники с равными основаниями и высотами.

Можно ли аналогичным образом преобразовать криволинейные фигуры? Кавальери представляет их себе состоящими из бесконечно тонких параллельных плоских слоев «неделимых» или «нитей» и утверждает, что площадь не меняется.

Приведем пример. Найти координаты центра масс полуокружности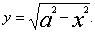

Решение. Вследствие симметрии 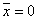 при вращении полуокружности вокруг оси ох получается сфера, площадь поверхности которой равна  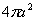а длина окружности равна 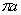. По теореме Гульдена имеем 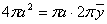. Отсюда  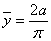т. е. центр масс С имеет координата .

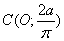Найти объём усечённой пирамиды с высотой 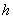и площадями верхнего и нижнего оснований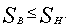

Решение. Если продолжить рёбра усечённой пирамиды, все они пересекутся в некоторой точке. Пусть ось ориентирована вдоль высоты пирамиды, начало координат — в плоскости верхней грани пирамиды. Тогда площадь сечений пирамиды 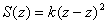 описывается квадратичной функцией. Чтобы задать произвольную квадратичную функцию (описывающую не только пирамиду), достаточно знать её значение в трех точках. Удобно использовать в качестве опорных верхнее и нижнее основание, приписав им координаты по равные и ,исреднее сечение (на половине высоты тела) с площадью 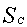. Для усечённой пирамиды все линейные элементы равны полу сумме соответствующих элементов оснований, поэтому из правил подобия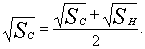

Это прямая призма с площадью 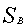, площадь сечения которой не зависит от , половина такой призмы с площадью основания 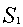. Её площадь сечения пропорциональна . И обычная пирамида с площадью основания 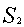, площадь сечения которой пропорциональна . Приравняем значения суммарной площади тел сравнения и исследуемой усечённой пирамиды в трёх точках по 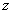. При  обе площад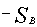и , при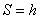получим  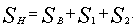При 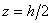 получим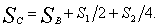

Для выбранных таким образом тел площади сечения при любом совпадают, поэтому объём усеченной пирамиды равен сумме объёмов тел сравнения:

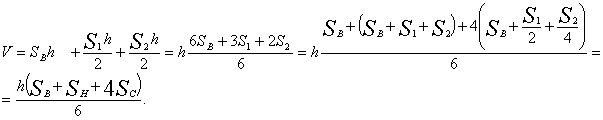
Эту формулу называют формулой Ньютона — Симпсона. Для усечённой пирамиды: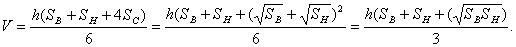

Литература:

1.         И. Ф. Шарыгин. Геометрия. Стереометрия. 10–11 кл.: Пособие для учащихся. –М.: Дрофа, 1998. — 272 с.

2.         В. В. Прасолов, И. Ф. Шарыгин. Задачи по стереометрия. –М.: «НАУКА», 1989, Библиотека математического кружка, вып. 19. — 287 с.

3.         Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10–11: М. Просвещение, 2004.

4.         Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Шестаков С. А., Юдина И. И. Планиметрия. Пособие для углублённого изучения математике.-М.: ФИЗМАТЛИТ, 2005.

5.         Маркущевич А.И «Детская энциклопедия. Мир небесных тел, Числа и фигура» М.: Педагогика 1972-г.