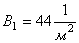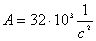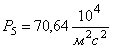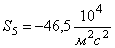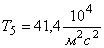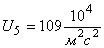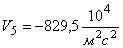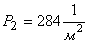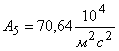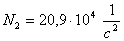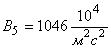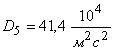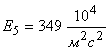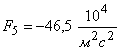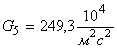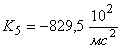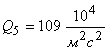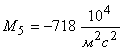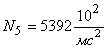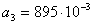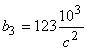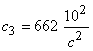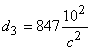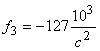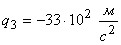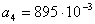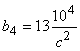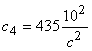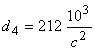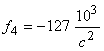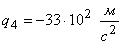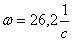Выполнено математическое моделирование процесса удара батанного механизма ткацких станков типа АТ в обе замочные пружины. Рассмотрена модель, в которой коленчатый вал и брус батана считаются упругими телами. Приведены результаты расчетов и сравнительные экспериментальные данные.
Ключевые слова: математическое моделирование; батанный механизм; пружина замка; упругость; коленчатый вал; брус батана; масса; степень свободы.
В работе [1] исследован установившийся режим движения батанного механизма ткацких станков типа АТ с учетом упругости коленчатого вала и бруса батана, а в настоящей работе рассматривается удар батана в замки (рис.1,a) — мгновенный останов машины на полном ходу при максимальной скорости батана по требованиям технологии ткачества [2]. При этом из-за упругости звеньев механизма удар начинается с левой замочной пружины механизма (см.рис.1,б). Этот процесс условно можно разделить на следующие основные этапы: 1) движение механизма при сопротивлении левой замочной пружины до начала удара в правую замочную пружину; 2) движение механизма при сопротивлении обеих замочных пружин: а) до крайнего переднего положения механизма; б) в обратном направлении до нарушения контакта с правой пружиной; 3) последующее движение механизма, состоящее из ряда этапов, носящее затухающий характер в силу рассеивания энергий.
Наибольшие усилия в звеньях механизма при ударе в замки появляются во время второго этапа в крайнем переднем положении механизма, поэтому здесь исследуются только первые два этапа. Начальными условиями при рассмотрении этих этапов соответственно являются конечные условия установившегося движения перед началом удара батана в замки и конечные условия первого этапа. При решении задачи удара местные деформации соударяющихся звеньев механизма считаются малыми и не учитываются, учитываются только общие деформации упругих звеньев: коленчатого вала, бруса батана и замочных пружин.
Рассмотрим процесс удара батанного механизма в обе замочные пружины с учетом крутильной упругости коленчатого вала между кривошипами и изгибной упругости бруса батана между шатунами [1,3]. Принятая динамическая модель механизма приведена на рис.1,б,в и представляет собой шестимассовую систему с четырьмя упругими звеньями, имеющую четыре степени свободы и отличающуюся от расчетной схемы установившегося движения тем, что на неё дополнительно наложены две упругие связи — замочные пружины и отключен двигатель станка.
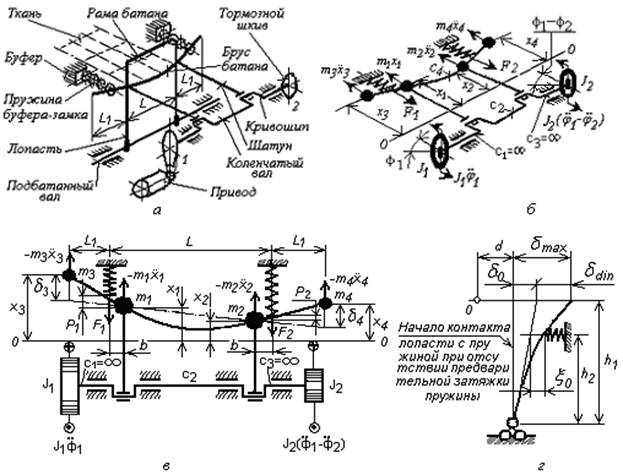
Рис.1. Принципиальная схема (а), динамическая модель (б,в) и деформация лопасти (г) батанного механизма в момент начала удара в замки
Если в расчетной схеме (см.рис.1,б) положить 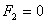 , то в этом случае получим расчетную схему для первого этапа удара в замки. Хотя система имеет четыре степени свободы и её положение в любой момент времени вполне определяется четырьмя обобщенными координатами, удобно при выводе уравнений, описывающих движения масс системы, пользоваться шестью координатами по количеству масс. Поскольку установившееся движение и удар батана в замки являются непрерывным процессом, то для математического описания удара используется та же система координат, что и в работе [1]: х1, х2, х3, х4 — перемещение соответствующей массы от ее заднего крайнего положения 0–0 в момент начала движения (см.рис.1,б,в);
, то в этом случае получим расчетную схему для первого этапа удара в замки. Хотя система имеет четыре степени свободы и её положение в любой момент времени вполне определяется четырьмя обобщенными координатами, удобно при выводе уравнений, описывающих движения масс системы, пользоваться шестью координатами по количеству масс. Поскольку установившееся движение и удар батана в замки являются непрерывным процессом, то для математического описания удара используется та же система координат, что и в работе [1]: х1, х2, х3, х4 — перемещение соответствующей массы от ее заднего крайнего положения 0–0 в момент начала движения (см.рис.1,б,в); 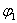 - угол поворота левого кривошипа;
- угол поворота левого кривошипа; 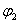 - упругий угол поворота правого кривошипа относительно левого за счет упругости коленчатого вала. Массы
- упругий угол поворота правого кривошипа относительно левого за счет упругости коленчатого вала. Массы 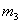 и
и 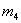 являются приведенными массами при рассмотрении свободных колебаний рамы батана [3].
являются приведенными массами при рассмотрении свободных колебаний рамы батана [3].
Остальная масса рамы батана с соответствующим приведением включена в массы 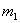 и
и 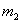 ;
; 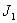 и
и 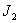 соответственно приведенный момент инерции деталей механизма, связанных с левым и правым концом коленчатого вала; F1 и F2 — приведенные к оси бруса батана силы упругости пружин и лопастей;
соответственно приведенный момент инерции деталей механизма, связанных с левым и правым концом коленчатого вала; F1 и F2 — приведенные к оси бруса батана силы упругости пружин и лопастей; 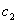 — коэффициент крутильной жесткости коленчатого вала между кривошипами;
— коэффициент крутильной жесткости коленчатого вала между кривошипами; 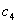 — изгибная жесткость бруса батана;
— изгибная жесткость бруса батана; 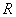 — радиус кривошипа;
— радиус кривошипа; 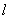 — длина шатуна;
— длина шатуна; 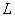 — пролёт бруса;
— пролёт бруса; 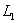 — длина консоли бруса. Принято
— длина консоли бруса. Принято 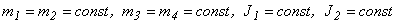 .
.
Ударная нагрузка воспринимается замочной пружиной, которая имеет предварительную затяжку [2]. Для вывода уравнений движения механизма необходимо предварительно найти приведенную к оси бруса силы упругости пружин и лопастей 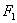 и
и 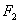 . Перемещения точек приложения сил F1 и F2 (см.рис.1,г) равны
. Перемещения точек приложения сил F1 и F2 (см.рис.1,г) равны 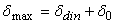 , где
, где 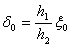 — заданная величина перемещения точек F1 и F2 за счет предварительной затяжки пружины
— заданная величина перемещения точек F1 и F2 за счет предварительной затяжки пружины 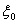 . Динамические деформации лопасти и пружины
. Динамические деформации лопасти и пружины 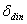 определяются как
определяются как
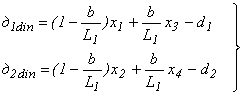
а выражения для определения перемещений точек приложения сил F1 и F2 имеют вид:
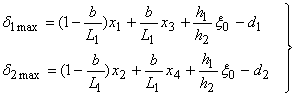
Силы упругости пружин F1 и лопастей F2, приведенные к оси бруса батана, определяются по формулам:
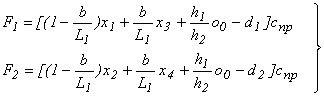
Жесткость замочной пружины и лопасти 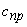 , приведенные к оси бруса батана, определяется выражением:
, приведенные к оси бруса батана, определяется выражением:
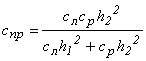
где 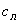 - изгибная жесткость лопасти;
- изгибная жесткость лопасти; 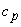 - жесткость замочной пружины.
- жесткость замочной пружины.
Движения масс 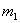 и
и 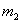 (см.рис.1,б,в) от крайнего заднего положения описываются уравнениями:
(см.рис.1,б,в) от крайнего заднего положения описываются уравнениями:
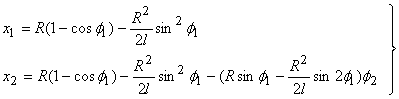 (1)
(1)
Рассмотрев движения приведенных масс коленчатого вала (см.рис.2,б) с моментами инерции 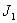 и
и 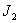 получаем следующие уравнения:
получаем следующие уравнения:
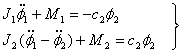 (2)
(2)
где 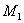 и
и 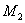 — скручивающие моменты коленчатого вала.
— скручивающие моменты коленчатого вала.
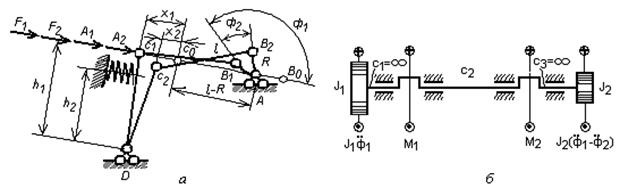
Рис.2. Расчетная схема кривошипно-шатунного механизма (а) и коленчатого вала (б) батанного механизма в момент начала удара в замки
Моменты 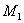 и
и 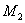 выражаются через реактивные силы
выражаются через реактивные силы 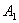 и
и 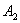 бруса батана на четырехзвенник (см.рис.2,а) на основании принципа возможных перемещений следующим образом:
бруса батана на четырехзвенник (см.рис.2,а) на основании принципа возможных перемещений следующим образом:
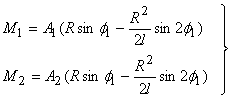 (3)
(3)
Реакции 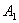 и
и 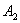 определяются из условия равновесия бруса батана, находящегося под действием сил инерции приведенных масс и приведенных к оси бруса сил сопротивления замочных пружин и лопастей F1 и F2 (см.рис.2,а):
определяются из условия равновесия бруса батана, находящегося под действием сил инерции приведенных масс и приведенных к оси бруса сил сопротивления замочных пружин и лопастей F1 и F2 (см.рис.2,а):
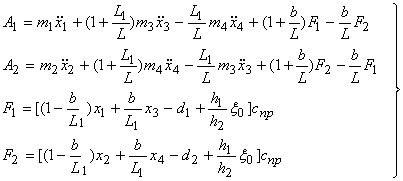 (4)
(4)
где 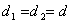 - расстояние точки приложения силы F1 и F2 от крайнего заднего положения 0–0 до положения в момент начала удара;
- расстояние точки приложения силы F1 и F2 от крайнего заднего положения 0–0 до положения в момент начала удара; 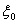 - величина предварительной затяжки замочной пружины (рис.1,г).
- величина предварительной затяжки замочной пружины (рис.1,г).
После подстановки выражений (3) в соотношения (2) с учетом (4) уравнения движения масс коленчатого вала принимают вид:
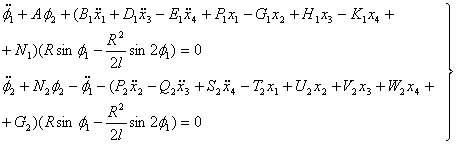 (5)
(5)
где
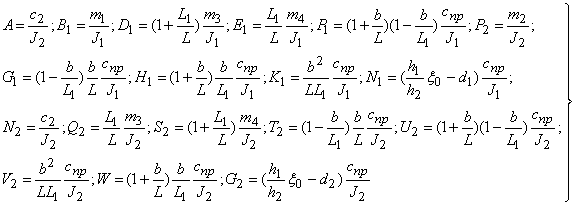
Уравнения движения масс 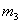 и
и 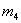 составляем следующим образом. Как видно из рис.1, брус батана под действием приложенных сил деформируется. Перемещение массы
составляем следующим образом. Как видно из рис.1, брус батана под действием приложенных сил деформируется. Перемещение массы 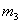 можно записать в виде:
можно записать в виде:
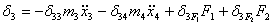 (6)
(6)
где 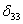 — перемещение массы
— перемещение массы 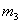 под действием силы
под действием силы 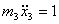 ,
, 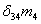 - перемещение массы
- перемещение массы 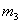 под действием силы
под действием силы 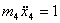 . Перемещения
. Перемещения 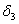 и
и 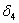 считаются положительными, а единичные силы направлены вдоль этих перемещений.
считаются положительными, а единичные силы направлены вдоль этих перемещений. 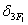 и
и 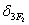 - соответственно перемещение массы
- соответственно перемещение массы 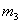 под действием силы
под действием силы 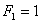 и
и 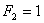 (направления сил показаны на рис.1,б). Соответствующая величина
(направления сил показаны на рис.1,б). Соответствующая величина 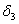 находится из геометрических соотношений
находится из геометрических соотношений
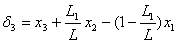 (7)
(7)
Приравнивая выражения (6) и (7) с учетом (4), получаем уравнение движения массы 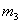 :
:
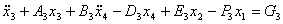 (8)
(8)
где
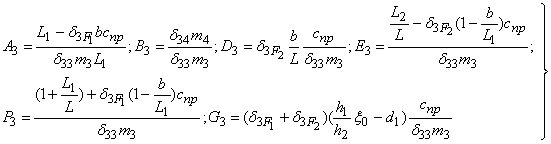 (9)
(9)
Аналогично находим уравнение движения массы 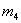 :
:
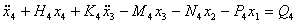 (10)
(10)
где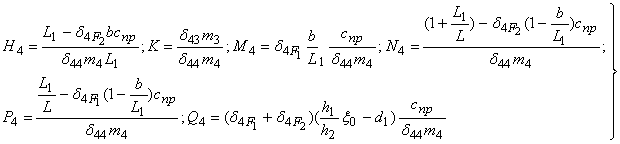
Из выражений (1) имеем:
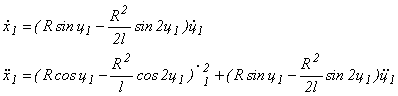
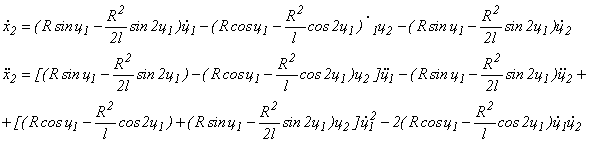 (11)
(11)
После преобразования выражений (5), (8), (10) с учетом (1) и (11) получаем следующую систему нелинейных дифференциальных уравнений второго порядка с переменными коэффициентами [4], описывающих движения масс расчетной схемы механизма при ударе в обе пружины замка:
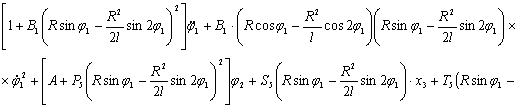
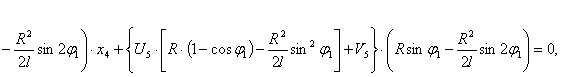
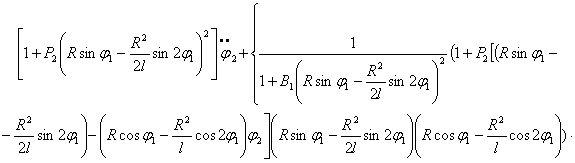
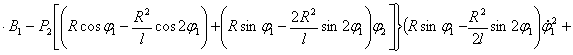
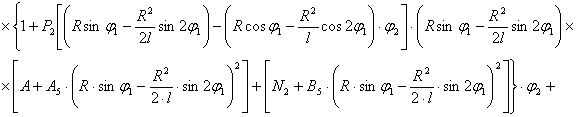
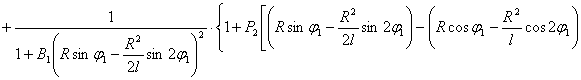 (12)
(12)
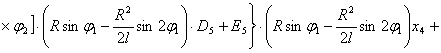
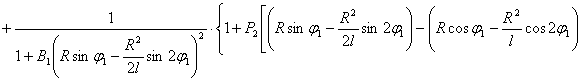

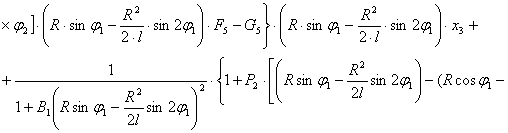
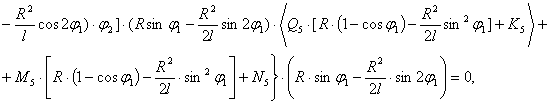
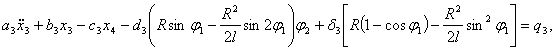
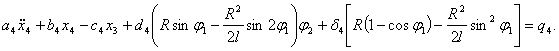
Начальные условия при 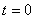 (получены в работе [1]):
(получены в работе [1]): 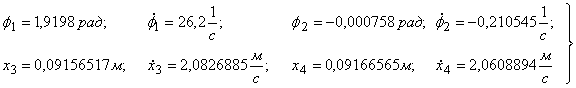
Общее решение такой системы неизвестно [4], и поэтому для ее решения воспользуемся численными методами интегрирования на ЭВМ. Сведём систему (12) к нормальной форме Коши, введя новые неизвестные функции 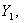
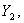
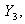
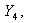
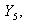
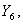
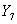 и
и 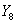 по следующим формулам:
по следующим формулам:
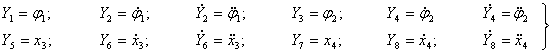
При этой замене система (1) переходит в систему восьми уравнений первого порядка, разрешённых относительно производных всех восьми искомых функций:
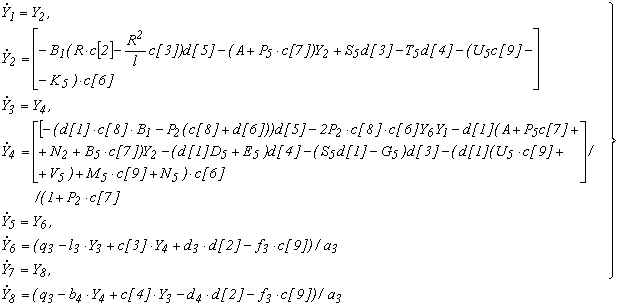 где коэффициенты суть данные непрерывные функции от
где коэффициенты суть данные непрерывные функции от 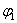 :
:
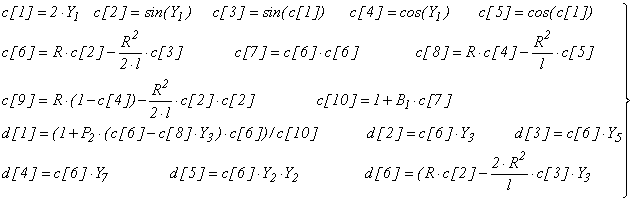 в частности некоторые из них — постоянные.
в частности некоторые из них — постоянные.
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
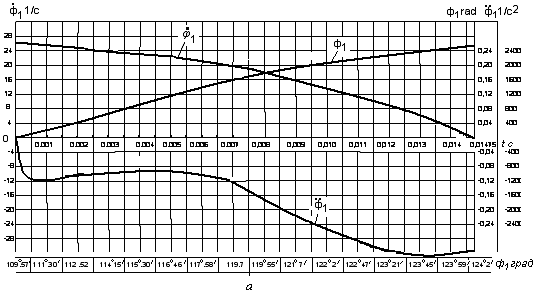
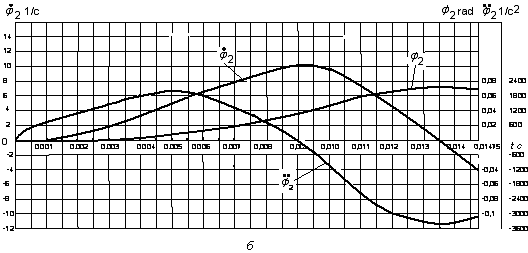
Рис. 3. Графики изменения угловых перемещений, скоростей и ускорений масс коленчатого вала с моментами инерции 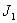 и
и 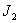
Уравнения решены численными методами [5] с использованием данных табл.1, соответствующих батанному механизму ткацкого станка АТ-127. Результаты решения представлены на рис.3 и 4. На рис.3,а,б приведены графики изменения угловых перемещений, скоростей и ускорений масс коленчатого вала с моментами инерции 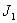 и
и 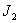 , а на рис.4,a,б,в,г приведены графики изменения линейных перемещений, скоростей и ускорений масс
, а на рис.4,a,б,в,г приведены графики изменения линейных перемещений, скоростей и ускорений масс 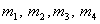 . Как видно из рис.3,а и рис.4,а, время движения массы с моментом инерции
. Как видно из рис.3,а и рис.4,а, время движения массы с моментом инерции 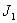 и массы
и массы 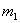 от момента начала удара до момента остановки масс при
от момента начала удара до момента остановки масс при 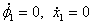 составляет 0,01475с. и за все это время угол
составляет 0,01475с. и за все это время угол 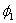 растет от нуля до
растет от нуля до 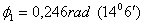 .
.
На рис.5 представлены схема расположения балочки на механизме для записи силы удара и осциллограмма удара батана в замки. Как видно из рис.5,б, длительность нарастания силы удара составляет 0,018с. Длительность нарастания силы удара, полученная в результате решения системы (12) составляет 0,01475с. и отличается от экспериментальных данных примерно на 18 %, что говорит о достаточно удовлетворительном согласовании результатов теории и эксперимента.
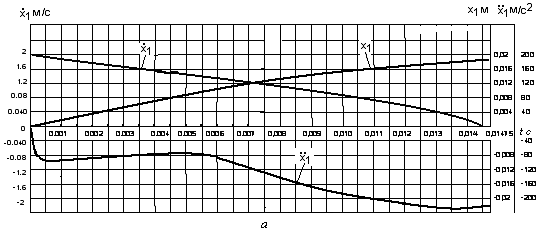
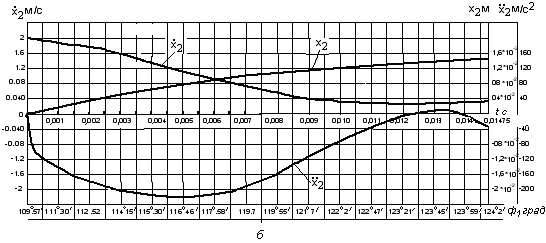
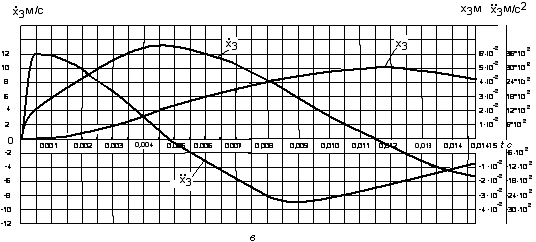
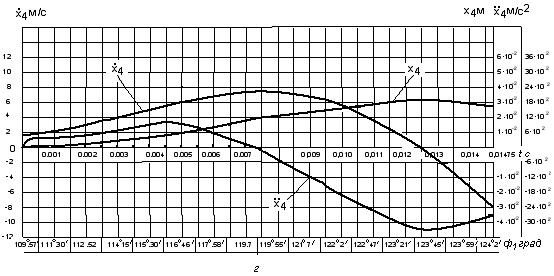
Рис. 4. Графики изменения линейных перемещений, скоростей и ускорений масс 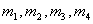
Рис. 5. Схема записи удара (а), осциллограмма силы удара батана в замки (б) и расчетная схема механизма при абсолютно жестких звеньях (в)
На рис. 3,б представлены законы относительно движения массы коленчатого вала с моментов инерции  . Как видно, диск
. Как видно, диск  совершает крутильные колебания, обусловленные наличием в кинематической цепи передачи упругого элемента. К моменту начала удара масса
совершает крутильные колебания, обусловленные наличием в кинематической цепи передачи упругого элемента. К моменту начала удара масса 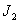 была повернута относительно массы
была повернута относительно массы 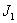 на угол
на угол 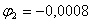 рад. Эта величина пренебрежимо мала и, следовательно, можно считать, что батан при ударе в замки одновременно касается обеих пружин, что достаточно хорошо согласовывается с экспериментом (см.рис.5,б).
рад. Эта величина пренебрежимо мала и, следовательно, можно считать, что батан при ударе в замки одновременно касается обеих пружин, что достаточно хорошо согласовывается с экспериментом (см.рис.5,б).
С момента начала удара батана в замки правая масса коленчатого вала 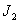 начинает поворачиваться (отставать) относительно левой массы
начинает поворачиваться (отставать) относительно левой массы 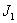 и в момент времени
и в момент времени 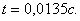 упругий угол
упругий угол 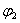 достигает максимального значения
достигает максимального значения 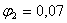 rad (φ2=4˚). В этот момент относительная скорость
rad (φ2=4˚). В этот момент относительная скорость 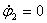 и массы
и массы 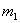 и
и 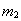 имеют одну и ту же скорость
имеют одну и ту же скорость 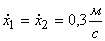 . При дальнейшем движении батана упругий угол
. При дальнейшем движении батана упругий угол 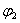 уменьшается, скорость
уменьшается, скорость 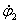 становится отрицательной, т. е. масса
становится отрицательной, т. е. масса 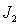 движется в направлении вращения массы
движется в направлении вращения массы 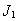 , и соответственно растет скорость движения массы
, и соответственно растет скорость движения массы 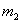 . В момент остановки масс
. В момент остановки масс 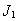 и
и 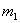 (
(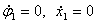 ) массы
) массы 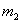 и
и 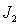 продолжают свое движение
продолжают свое движение 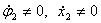 , (рис.3,б и рис.4,б).
, (рис.3,б и рис.4,б).
Из рис.4,в и 4,г видно, что массы 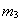 и
и 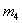 , достигают крайнего положения соответственно в моменты времени
, достигают крайнего положения соответственно в моменты времени 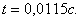 и
и 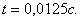 , т. е. раньше масс
, т. е. раньше масс 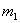 и
и 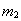 . Следовательно, при ударе батана в замки концы консолей заносятся вперед и раньше чем пальцы лопастей начинают обратное движение, т. е. брус совершает изгибные колебания.
. Следовательно, при ударе батана в замки концы консолей заносятся вперед и раньше чем пальцы лопастей начинают обратное движение, т. е. брус совершает изгибные колебания.
Из рис.4 видно, что законы движения масс 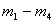 имеют явно выраженный колебательный характер. Если колебательный процесс слабо выражен в изменениях перемещений масс, то скорости и ускорения колебательного движения достигают заметной величины. Процесс колебательного движения масс объясняется наличием в кинематической цепи передачи упругих элементов.
имеют явно выраженный колебательный характер. Если колебательный процесс слабо выражен в изменениях перемещений масс, то скорости и ускорения колебательного движения достигают заметной величины. Процесс колебательного движения масс объясняется наличием в кинематической цепи передачи упругих элементов.
Как видно из рис.4,а и 4,б при ударе батана в замки массы 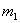 и
и 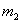 перемещаются на разные величины: масса
перемещаются на разные величины: масса 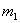 перемещается на большую величину (
перемещается на большую величину (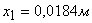 ), чем масса
), чем масса 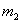 (
(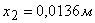 ). Расчётная схема механизма при абсолютно жёстких звеньях, представлена на рис.5,в, где
). Расчётная схема механизма при абсолютно жёстких звеньях, представлена на рис.5,в, где 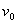 — начальная скорость удара;
— начальная скорость удара; 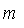 - приведённая масса механизма;
- приведённая масса механизма; 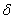 ,
, 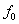 — податливость и предварительная затяжка пружины. Линейные перемещения, скорости и ускорения массы
— податливость и предварительная затяжка пружины. Линейные перемещения, скорости и ускорения массы 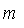 определяются по формулам:
определяются по формулам:
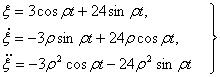 (13)
(13)
где 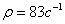 — круговая частота собственных колебаний массы на пружине.
— круговая частота собственных колебаний массы на пружине.
Расчётная схема рис. 5,в и выражения (13) заимствованы нами из работы [6]. Постоянные, входящие в (13), соответствуют батанному механизму станка 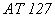 . Графики «идеальных» законов движения батанного механизма станка представлены на рис.6.
. Графики «идеальных» законов движения батанного механизма станка представлены на рис.6.
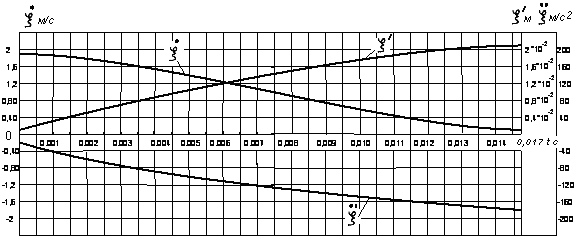
Рис. 6. Графики «идеальных» законов движения батанного механизма
Сравнивая рис.4 с рис.6 видим, что законы движения масс 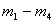 , рассчитанные с учетом упругости звеньев, значительно отличаются от законов движения массы
, рассчитанные с учетом упругости звеньев, значительно отличаются от законов движения массы 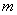 , рассчитанной по «идеальным» законам. Если изменения в перемещенных массах слабо выражены, то изменения скорости и ускорения достигают заметной величины. Максимальные значения ускорений масс m1 иm2 превышают «идеальное» ускорение массы примерно в 1,38 раза, а ускорения масс
, рассчитанной по «идеальным» законам. Если изменения в перемещенных массах слабо выражены, то изменения скорости и ускорения достигают заметной величины. Максимальные значения ускорений масс m1 иm2 превышают «идеальное» ускорение массы примерно в 1,38 раза, а ускорения масс 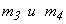 — в десять раз.
— в десять раз.
Выводы.
1. Выполнено математическое моделирование процесса удара батана в замки с учетом упругости звеньев.
2. Результаты численного решения полученных уравнений показывают, что законы движения механизма, рассчитанные с учетом упругости звеньев, значительно отличаются от «идеальных» законов движения.
3. Результаты теоретического исследования процесса удара в замки показывают, что длительность нарастания силы удара 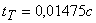 . Экспериментально установлено, что время нарастания силы удара
. Экспериментально установлено, что время нарастания силы удара 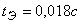 . Таким образом, результаты теоретического исследования подтверждаются экспериментальными данными.
. Таким образом, результаты теоретического исследования подтверждаются экспериментальными данными.
4. Результаты теоретического и экспериментального исследования удара батана в замки показывают, что а) сила удара батана левую пружину в 1,3…1,5 раза больше силы удара в правую пружину; б) величины максимальных динамических усилий в замочных пружинах 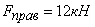 и
и 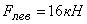 , рассчитанные с учетом упругости звеньев, значительно отличаются от сил удара
, рассчитанные с учетом упругости звеньев, значительно отличаются от сил удара 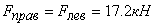 , полученных по «идеальным» формулам. Для левой пружины эта разница составляет 15 %, а для правой — 45 %. В заключение следует обратить внимание на то, что при расчете с учетом упругости звеньев представляется возможность более полно изучить происходящие в них явления и, следовательно, полнее учесть при проектировании механизма факторы, влияющие на выбор его параметров.
, полученных по «идеальным» формулам. Для левой пружины эта разница составляет 15 %, а для правой — 45 %. В заключение следует обратить внимание на то, что при расчете с учетом упругости звеньев представляется возможность более полно изучить происходящие в них явления и, следовательно, полнее учесть при проектировании механизма факторы, влияющие на выбор его параметров.
Литература:
1. Егодуров Г. С., Пнёв А. Г. К численной реализации дифференциальных уравнений с периодически изменяющимися параметрами // Вестник МГТУ им. Н. Э. Баумана. Сер. “Естественные науки”. 2010. № 2. — С. 58–64.
2. Малышев А. П., Воробьев. П. А. Механика и конструктивные расчеты ткацких станков. — М.: Машгиз, 1960. — 552 с.
3. Коритысский Я. И. Колебания в текстильных машинах.– М.: Машиностроение, 1973. — 320 с.
4. Агафонов С. А., Муратова Т. В. Обыкновенные дифференциальные уравнения. — М.: Издательский дом «Академия», 2008. — 240 с.
5. Турчак Л. И. Основы численных расчетов. — М.: Наука, 1987. -320 с.
6. Мартынов И. А. Некоторые вопросы динамики высокоскоростных ткацких станков в нестационарный период работы: Дис. канд. техн. наук. — МТИ, 1959. — 128 с.