Преобразования, происходящие в мире, стремительный технический прогресс предъявляют новые требования к молодым специалистам с высшим образованием. Растет потребность в высококвалифицированных, компетентных выпускниках, способных к сообразованию и саморазвитию. В связи с этим возникает необходимость в совершенствовании процесса обучения, начиная с целей профессионального образования и заканчивая методикой обучения.
Для формирования навыков самообразования важную роль играет мотивационный компонент обучения. В процессе преподавания курса математического анализа студентам экономических специальностей приходится встречаться с непониманием необходимости изучения многих его разделов. Преодолеть проблемы подобного рода и стимулировать мотивационную составляющую учебного процесса помогает демонстрация приложений изучаемого раздела соответствующая направлению подготовки студентов. При изучении дифференциальных уравнений это сделать очень просто.
Возможности применения дифференциальных уравнений можно показать на первых лекциях, первоначально изучив основные понятия и определения и рассмотрев основные методы их решения. Начать можно с модели естественного роста.
Существуют процессы, в которых величина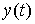 
такова, что скорость ее изменения пропорциональна значению этой величины в тот же момент времени. Уравнение такого процесса называют уравнением естественного роста:
.
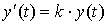Якоб Бернулли впервые вывел это уравнение и решил задачу: Пусть заимодавец платит кредитору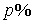 
от занятой суммы 
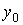в год. Сколько он должен уплатить за год на каждую единицу занятой суммы, если проценты нарастают непрерывно?
Величина долга растет со скоростью, пропорциональной значению этой величины в тот же момент времени, т. е. решаем уравнение с разделяющимися переменными
,
.
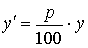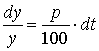Интегрируем полученное уравнение и получаем общее решение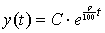 
. Для нахождения константы С пользуемся тем, что 
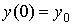. Дифференциальное уравнение естественного роста предложил Мальтус для прогнозирования роста населения Земли. Коэффициент k называют мальтузианским коэффициентом линейного роста.
Для формирования мотивации у студентов одного примера недостаточно, поэтому далее рассматриваем модель естественного роста выпуска продукции: найти закон роста выпуска дефицитной продукции в условиях не насыщаемости рынка.
Количество продукции, которая произведена в момент времени t, обозначим 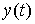. Предполагаем, что продукция реализуется по фиксированной цене p моментально. Доход в момент времени t равен 
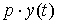. Предприятию выгодно расширять производство в связи с получением прибыли от реализации своей продукции.
Пусть на инвестиции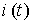 
в производство расходуется m-я часть дохода, т. е.
.
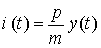Результатом расширения производства будет прирост дохода, m-я часть которого будет направлена на увеличение выпуска продукции. Это приведет к росту выпуска, причем скорость выпуска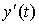 
будет пропорциональна увеличению инвестиций, т. е.
.
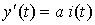Таким образом, получим дифференциальное уравнение естественного роста
,
.
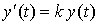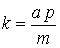Решением его является экспоненциальная функция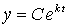 
, показывающая, как можно быстро добиться огромных объемов выпуска дефицитной продукции, если постоянно направлять часть дохода в расширение производства.
Харрод и Домар считали, что можно добиться устойчивого роста всей мировой экономики, так как устойчивый темп роста производства обеспечивается естественным ростом населения, естественным ростом производительности труда и увеличением размера накопления капитала.
Модели естественного роста описываются экспоненциальной функцией. Темпы роста, описываемые ей, со временем замедляются, и наступает период насыщения. В связи с этим возникла необходимость в изменении модели роста.
Дж. Кьютелет считал, что константа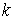 
в уравнении естественного роста должна быть убывающей функцией, зависящей от :
.
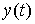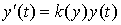Основываясь на это предположение, в 1836 г. его ученик Ферхюльст для роста населения предложил использовать уравнение
,
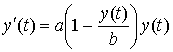т. е. считать, что
.
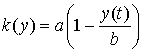Разделяя переменные, находим
, 
.
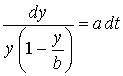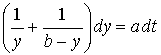Проинтегрировав это соотношение, получаем
,
.
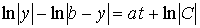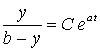Отсюда следует, что
.
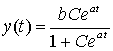Полученную функцию называют логистической кривой. При малых значениях t логистический рост подобен естественному росту, а при больших t характер роста изменяется и темпы роста замедляются. При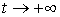 
кривая приближается, но не пересекает прямую 
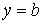, которая является стационарным решением уравнения и соответствует случаю
.
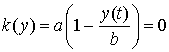Полезно будет рассмотрение и модели «социальной диффузии». Известно, что рынки информации и товаров подвержены насыщению. Количество сторонников нечто нового описывается законом Ферхюльста. Но в какой-то момент времени наступает насыщение рынков и эффективность от агитации и рекламы уменьшается. Хотя число сторонников нечто нового с течением времени стремится к постоянному числу.
Уравнение Ферхюльста в социальных науках применяется для представления распространения в определенных социальных группах образцов поведения, моды, информации (рекламы), культурных новшеств. При изучении социальных групп, это уравнение называют уравнением Дж. Коулмена. Так как он уточнил смысл коэффициентов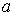 
и 
и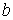з уравнения Ферхюльста, применяя его к социальным группам. Дж. Коулмена предложил следующее уравнение:
,
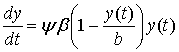где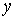 
— число сторонников новшества в данный момент времени; 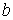— общая численность рассматриваемой группы; 
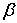— число контактов, завязываемых каждым сторонникам новшества в единицу времени; 
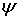— коэффициент, меняющийся от 0 до 1 и отражающий то, что не каждый контакт сторонника с не сторонником предполагает агитацию последнего, а также то, что не каждая агитация заканчивается успехом.
Важно отметить, что эмпирические исследования подтверждают, что увеличение сторонников нового изменяется согласно уравнению Ферхюльста (Коулмена).
В отличие от модели естественного роста и от модели Дж. Кьютелета, когда соответственно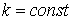 
и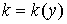 
, в модели, описывающей рост количества продукции 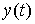на некотором предприятии, произведенной в момент времени , предполагаем, что коэффициент 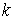зависит от времени 
: 
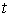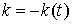. Знак «минус» указывает на то, что фонды сокращаются. Сокращение фондов происходит, когда предприятие не вкладывает часть вырученной прибыли в производство, и со временем на нём происходит изнашивание оборудования и орудий труда, т. е. происходит убытие фондов.
Тогда рост количества продукции 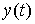на некотором предприятии, произведенной в момент времени 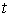описывается уравнением
, 
.
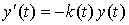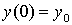Возможно два случая. Первый, когда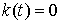 
, и второй, когда 
.
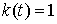1. Пусть фонды в указанный промежуток времени не убывают, 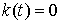. Следовательно, из-за отсутствия капиталовложений производство увеличиваться не будет, а ввиду отсутствия фондов оно не должно и убывать. Таким образом, объем производства должен остаться на прежнем уровне. Что и дает решение дифференциального уравнения 
: 
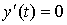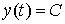(производственная константа).
Так как 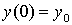, то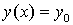 
.
2. При постоянном убытии фондов, при 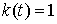, должно происходить снижение производства. Решение соответствующего дифференциального уравнения подтверждает это:
; 
;
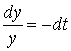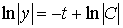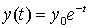(убывающая функция).
Уравнением 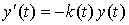пользуются в социальных науках и страховом деле для определения шанса того, что человек доживет до возраста 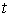. Решением этого уравнения при начальном условии 
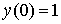является функция
.
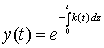Таким образом, демонстрация возможности применения дифференциальных уравнений обеспечивает усиление мотивационной составляющей учебного процесса и существенно влияет на усвоение студентами данного раздела математического анализа. Интерпретация экономических и социальных процессов с помощью математического языка подготавливает студентов к моделированию реальных процессов. Кроме того, способствует формированию системы знаний и операционных умений, используемых для решения задач, возникающих при выполнении основных видов профессиональной деятельности и развитию личностных качеств, необходимых для высококвалифицированных специалистов.
Литература:
1. Ахтямов А. М. Математика для социологов и экономистов: Учеб.пособие / Под редакцией Бунатяна Р. А. — М.: ФИЗМАТЛИТ, 2004. — 464с.
2. Куимова Е. И., Ячинова С. Н. Особенности преподавания курса дифференциальных уравнений студентам экономических специальностей / Материали за 9-а международна практична конференция «Научният потенциал на света-2013» Т.11. Педагогически науки. София: «Бял ГРАД-БГ» ООД, 2013. — С.27–29.
3. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах // Молодой ученый № 12(59), 2013, С.3–6.
