Основная задача работы — синтез виртуальной модели для нахождения оптимального пути робота в заданном многопараметрическом пространстве. Цель — постановка компьютерной лабораторной работы, связанной с решением задач линейного и дискретного программирования при управлении роботами. Предполагается, что робот должен обойти множество контрольных пунктов с учетом заданных критериев: минимум пройденного пути, времени движения, погрешности выхода в контрольные пункты.
Ключевые слова:робот; задача коммивояжера; метод ветвей и границ; минимизация; оптимальный путь обхода; Delphi; лабораторная работа.
Введение. Качество обучения является одним из основных объектов стратегии образования. Оно определяет репутацию и имидж ВУЗа. Выпускники учебного заведения с высоким качеством обучения обладают широким кругом знаний и являются высококвалифицированными специалистами [1]. Для повышения уровня образования необходимо проектирование методического и материально-технического обеспечения лабораторных циклов, в том числе и по робототехническому направлению.
Наличие программной интегрированной обучающей среды с удобным пользовательским интерфейсом во многих случаях позволяет заменить использование реальных дорогостоящих технологических объектов адекватными, по требуемым параметрам, компьютерными моделями, активизировать самостоятельную работу при выполнении практических и лабораторных работ, автоматизировать промежуточный контроль знаний студентов.
При проектировании обучающей среды возникают достаточно противоречивые требования [6]. Наиболее существенными из них представляются:
- создание дидактических средств для приобретения навыков работы с исследуемыми объектами;
- гибкость комплектования лабораторных установок объектами исследования;
- обеспечение мер безаварийной эксплуатации исследуемых объектов в процессе выполнения работы и при непреднамеренных нарушениях режимов;
- стоимость технического обеспечения лабораторного цикла;
- возможность тиражирования и поставки средств обеспечения лабораторных циклов потребителям.
Обучающие модули и специализированные программы позволяют визуализировать учебную информацию, моделировать и имитировать изучаемые процессы или явления, проводить лабораторные работы в условиях имитации реального опыта на компьютере, формировать умение принимать оптимальное решение в различных ситуациях, усилить мотивацию обучения и др. [6].
Разработка методического обеспечения в области робототехники должна учитывать возросший во всем техническом мире интерес к интеллектуальным системам, приведшим к появлению спортивных соревнований среди мобильных роботов [4]. Идея заключается в том, что роботы должны обойти все маяки, причем качество управления оценивается по некоторому критерию, например, — полный обход за кратчайшее время. Оптимизация критерия может производиться методами линейного или дискретного программирования. В результате должна быть получена оптимальная траектория движения робота.
Разработчик систем управления роботами должен уметь оптимизировать выбранные параметры движения, поэтому в настоящей статье предложена компьютерная модель, позволяющая задавать опорные точки и строить траекторию движения робота в соответствии с определёнными критериями. Данная модель может использоваться с автоматизированной адаптивной обучающей системой [6], имеющей четыре раздела: обучение, текущий контроль знаний студента, выполнение лабораторной работы, проверка результатов решения студентом задачи оптимизации траектории движения робота. Адаптация системы проявляется в том, что траектории обучения изменяется в зависимости от уровня знаний конкретного студента и, кроме того, ответы на вопросы могут быть не строго формализованы и не строго детерминированы.
В математике задача обхода контрольных точек по кратчайшему пути носит название «Задача о коммивояжере» [3].
1. Постановка задачи. Классическая постановка задачи о коммивояжере выглядит следующим образом:
Имеется N городов, выезжая из исходного города А1, коммивояжер (в нашем случае это будет транспортный робот) должен побывать во всех городах по 1 разу и вернуться в город А1. Задача заключается в определении последовательности объезда городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время пути, суммарное расстояние и т. д.
Для расчета затрат существует матрица условий, содержащая затраты на переход (в общем случае) из каждого города в каждый, при этом не допускается переход из j-го города в j-ый (в матрице диагональные элементы исключаются). Целью решения является нахождения маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат [3].
Чтобы привести задачу к удобному виду, введём некоторые термины. Итак, города перенумерованы числами jÎ Т = (1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t = (j1, j2,..., jn, j1), причём все j1..jn — разные номера; повторяющийся в начале и в конце j1,показывает, что перестановка зациклена. Расстояния между парами вершин Сijобразуют матрицу С. Задача состоит в том, чтобы найти тур t, минимизирующий функционал:
(1)
Относительно формулировки задачи уместно сделать два замечания.
Во-первых, в постановке Сijозначали расстояния, поэтому они должны быть неотрицательными, т. е. для всех jÎТ:
Сij³0; Cjj=∞ (2)
симметричными, т. е. для всех i, j:
Сij= Сji
и удовлетворять неравенству треугольника, т. е. для всех:
Сij+ Сjk³Cik(3)
Второе замечание касается числа всех возможных туров. В несимметричной задаче все туры t = (j1, j2,..., jn, j1) и t’ = (j1, jn, …,j2, j1) имеют разную длину и должны учитываться оба. Разных туров очевидно (n-1)!.
2. Метод решения задачи. Для решения данной задачи был использован метод “ветвей и границ” [3], являющийся одним из основных для решения задач дискретного программирования. В табл. 1 приведена матрица параметров траектории (например, расстояние, экономические затраты и т. п.) для простого примера [5].
Суть идеи проста. Все перебираемые варианты следует разбить на классы (блоки), сделать оценку снизу (при минимизации) для всех решений из одного класса, и если она больше ранее полученной, то отбросить все варианты из этого класса. Весь вопрос в том, как разделять на классы. Например,
Таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
¥ |
7 |
3 |
10 |
17 |
5 |
|
2 |
9 |
¥ |
4 |
5 |
8 |
6 |
|
3 |
13 |
2 |
¥ |
9 |
11 |
14 |
|
4 |
5 |
8 |
6 |
¥ |
3 |
6 |
|
5 |
16 |
11 |
13 |
10 |
¥ |
8 |
|
6 |
6 |
5 |
9 |
8 |
4 |
¥ |
Если мы будем вычитать одно и то же число из всех элементов строки или столбца, то суммарная оценка пути коммивояжера не изменится. При вычитании константы из элементов строки оценка любого пути уменьшится на эту константу, ибо числа в строке соответствуют выезду из города. Точно так же и вычитание из элементов столбца — въезд в город. Вычитаемая константа входит в оценку пути, но не рассматривается дальше, после изменения матрицы. Найдем минимум в каждой строке (в первой строке — это 3, во второй — 4 и т. д.) и вычтем его. Сумма вычитаемых констант равна 24. Получается матрица:
Таблица 2
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
¥ |
4 |
0 |
7 |
14 |
2 |
|
2 |
5 |
¥ |
0 |
1 |
4 |
2 |
|
3 |
11 |
0 |
¥ |
7 |
9 |
12 |
|
4 |
2 |
5 |
3 |
¥ |
0 |
3 |
|
5 |
8 |
3 |
5 |
2 |
¥ |
0 |
|
6 |
2 |
1 |
5 |
4 |
0 |
¥ |
Аналогичную операцию выполним со столбцами: из элементов первого вычитаем 2, а из элементов четвертого — 1. Итого — вся сумма — 27. Все пути коммивояжера уменьшились на это значение.
Таблица 3
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
¥ |
4 |
0 |
6 |
14 |
2 |
|
2 |
3 |
¥ |
0 |
0 |
4 |
2 |
|
3 |
9 |
0 |
¥ |
6 |
9 |
12 |
|
4 |
0 |
5 |
3 |
¥ |
0 |
3 |
|
5 |
6 |
3 |
5 |
1 |
¥ |
0 |
|
6 |
0 |
1 |
5 |
3 |
0 |
¥ |
Если получается выбор по одному нулю в каждом столбце и строке (они выделены в матрице), то тем самым мы получаем путь коммивояжера с оценкой 27. Это путь (1->3->2->4->5->6->1) с минимальной оценкой, любой другой путь имеет большую оценку. Значение 27 — это оценка снизу всех маршрутов коммивояжера. В данном случае она достигается на конкретном маршруте.
3. Реализация метода при помощи пакета программирования Delphi.
На рис. 1 представлено главное окно интерфейса программного модуля для выполнения лабораторной работы «Планирование оптимального маршрута транспортного робота».
Программа реализована в интегрированной среде визуального программирования Delphi 7 [2].
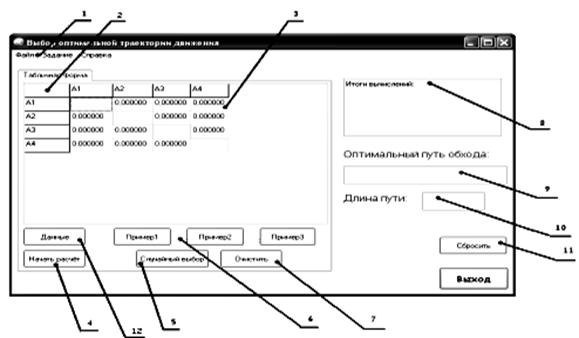
Рис. 1. Окно программы «Выбор оптимальной траектории движения робота»
На модели расположены:
1. Основное меню программы. Главное меню приложения включает в себя следующие пункты:
- Меню «Файл» имеет стандартные операции и представлено на рис.2

Рис.2. Меню «Файл».
- Меню «Задание» представлено на рис.3
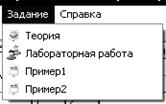
Рис.3. Меню «Задание»
- Теория — содержит основную информацию, необходимую для выполнения лабораторной работы;
- Лабораторная работа — на этой форме отображается задание к лабораторной работе и алгоритм её выполнения;
- Пример1/Пример2 — наглядно иллюстрируют ход решения;
- Меню «Справка» — краткая информация о программе «Планирования оптимального маршрута транспортного робота»».
2. Фиксированные ячейки — отображают количество пунктов назначения, через которые необходимо пройти транспортному роботу.
3. Табличная форма — содержит матрицу расстояний между городами. Элементы матрицы могут задаваться пользователем или генерироваться автоматически.
4. Кнопка «Начать расчёт» подразумевает, что после её нажатия будет выводиться оптимальное решение.
5. Кнопка «случайный выбор» формирует новое задание в виде матрицы расстояний (случайные величины в диапазоне от 0 до 20).
6. Кнопки «Пример1», «Пример2», «Пример3» — открывают априори заданные варианты трех лабораторных работ соответственно. Здесь матрицы зафиксированы, в отличие от тех, что были получены при нажатии кнопки «случайный выбор».
7. Кнопка «Очистить» освобождает поле матрицы расстояний для ввода новых значений.
8. Данное окно предназначено для ввода вручную результата решения студентом задачи оптимизации маршрута. Оно позволяет вводить ответ в виде текста с клавиатуры, загружать его из файла, редактировать и сохранять в файл.
9–10. Поля для вывода машинного решения задачи оптимизации: «оптимальный путь обхода» и «длина пути».
11. Кнопка «Сбросить» очищает элемент (8) и предоставляет возможность проводить последующие вычисления.
12. Кнопка «Данные» позволяет выводить на экран окно, предназначенное для задания параметров таблицы (рис.4).
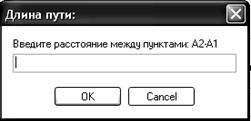
Рис.4 Параметры таблицы
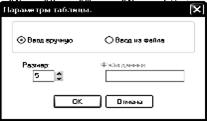
Рис.5 Длина пути
Заполнение таблицы производится двумя способами: «Ввод вручную» и «Ввод из файла».
- В 1-м случае размер матрицы расстояний регулируется нажатием стрелки «вверх/вниз», т. е. изменяется количество пунктов назначения. В появившемся окне (рис.5) прописываем необходимое значение.
- Во 2-м случае в поле «Файл данных» вводится адрес ранее сохранённого файла.
4. Пример решения задачи. Имеются 6 пунктов назначения. Транспортному роботу необходимо развести груз, используя оптимальную траекторию движения. Ниже приведена несимметричная матрица расстояний, т. е. проезд одной дороге из города А в город В может быть не равен проезду по другой дороге из А в В:

В ходе лабораторной работы студенты производят аналитические вычисления (см. пункт 2 — метод решения задачи) и получают определённый результат. Далее необходимо проверить правильность проделанных решений. Данные из матрицы заносятся в таблицу программы. На рисунке 6 показаны результаты примера. Очевидно, что если полученные «длина пути» и «оптимальный путь обхода» полностью совпадают с произведенными ранее аналитическими вычислениями, то работа выполнена верно.
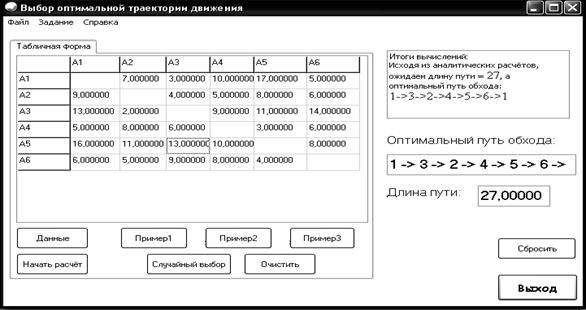
Рис. 6. Результаты
Заключение
Была создана компьютерная модель, позволяющая находить оптимальную (по заданному критерию) траекторию обхода определенного количества опорных точек. Используемый метод оптимизации — «Метод ветвей и границ» [3].
Модель позволяет задавать размер матрицы расстояний (она может быть и несимметричной), вводить данные вручную или считывать из файла. После команды «Пуск» рассчитывается минимальный путь обхода опорных точек, и результат выдается преподавателю. Также модель осуществляет проверку решений студента.
Литература:
1. Афанасьева Э. В., Раводин О. М. Болонский процесс в России: за и против. // Технологии и методики образования. 2011. № 2.. C.7–8
2. Бобровский С. И., Delphi 7. Учебный курс — СПб.: Питер, 2006. — 736с.: ил.
3. Задача коммивояжёра [Электронный ресурс] // Википедия: свободная энцикл. — Электрон. дан. — [Б. м.], 2012. –URL: http://ru.wikipedia.org/wiki/ %C7 %E0 %E4 %E0 %F7 %E0_ %EA %EE %EC %EC %E8 %E2 %EE %FF %E6 %B8 %F0 %E0 (дата обращения: 20.10.2012).
4. Мобильные роботы [Электронный ресурс] // Официальный сайт молодежного научно-технического фестиваля «Мобильные роботы». URL: http://www.mobilerobots.msu.ru/ru/regulations2010main.html (дата обращения: 21.10.2012).
5. Окулов С. М. Программирование в алгоритмах, — М.: БИНОМ. Лаборатория знаний, 2002. — 341 с: ил.
6. Раводин О. М., Туровец Л. А., Зайцев А. П. Адаптивная обучающая система для проведения лабораторных практикумов при дистанционной технологии // Успехи современного естествознания. 2005. № 6 C. 90–92.







