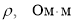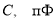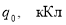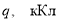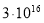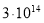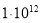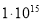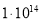Расчет тепловых потерь сферического конденсатора



В статье рассматриваются особенности сферических конденсаторов со слабопроводящими средами.

Ключевые слова : конденсатор, тепловая энергия, потери, заряд.

Развитие физики как фундаментальной точной науки способствует качественному освоению курсантами специальных дисциплин, формированию научного мышления и самостоятельному совершенствованию в будущей профессиональной деятельности военных инженеров. В условиях проведения СВО траектория практического применения физики представляет собой линию движения и образовательного процесса военных вузов как на аудиторных занятиях, так и в системе военно-научной работы курсантов.

Деятельность обучающихся в рамках военно-научного общества направлена на формирование, развитие и осуществление самостоятельного приобретения научных знаний при решении технических задач на основе физических законов, например, электродинамики. Её закономерности заложены в принципы функционирования авиационного оборудования для получения электрических импульсов с помощью схем, содержащих конденсаторы.

Конденсатор — пассивный электронный компонент электрической схемы. Конструктивно конденсаторы изготовляют в виде токопроводящих обкладок, разделенных диэлектриком. Сферический конденсатор состоит из двух концентрических шаровых обкладок, разделенных сферическим слоем диэлектрика, толщина которого мала по сравнению с размерами обкладок. Если внутреннюю обкладку подобного конденсатора зарядить, внешнюю — заземлить, то, пренебрегая краевыми эффектами, его поле будет радиально-симметричным и сосредоточенным только между обкладками [1, с. 77].

Сферические конденсаторы имеют применение в геофизических исследованиях почвы при строительстве аэродромов, в слаботочных высоковольтных источниках питания установок по ремонту военной технике в полевых условиях (например, электростатическое промасливание, порошковая окраска). Они предназначены для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт [2].

Определим для сферического конденсатора временную зависимость заряда на внутренней обкладке сферического конденсатора и выделившуюся тепловую энергию при растекании заряда.

Напряженность поля сферы определяется выражением, аналогичным формуле точечного заряда,

, (1)

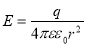
где — расстояние от центра конденсатора, — радиус внутренней обкладки сферического конденсатора, х — расстояние от поверхности внутренней сферы до точки наблюдения; ε — диэлектрическая постоянная вакуума; ε ₀ — диэлектрическая проницаемость среды; q — величина заряда в момент времени t .

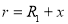
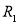
Запишем закон Ома в дифференциальной форме через величины, характеризующие электрическое состояние среды в конкретной точке,

, (2)

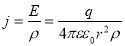
где j — плотность тока; ρ — удельное сопротивление.

Модуль вектора плотности тока j в данной точке через площадку, расположенную перпендикулярно направлению движения носителей заряда, прямо пропорционален силе тока I и обратно пропорционален площади этой площадки S [3, с. 181].

Следовательно, с учетом равенств (1) и (2) можно записать выражение для силы тока на расстоянии r от центра сферического конденсатора

. (3)

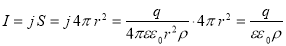
Если конденсатор замкнуть, то потечёт ток за счёт убыли заряда на внутренней сферической обкладке. Дифференциальное уравнение для изменения заряда на обкладках конденсатора в этом случае будет иметь вид

. (4)

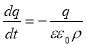
Проинтегрируем равенство (4) по времени от 0 до t, учитывая, что величина заряда изменилась от q ₀ до q

(5)

(6)

(7)

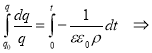
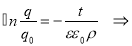
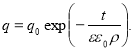
Как видно из формулы (7), временная зависимость заряда устанавливается не размерами сферических обкладок конденсатора, а диэлектрической проницаемостью ε и удельным сопротивлением ρ изоляционного слоя устройства. В таблице 1 представлены слабопроводящие среды, используемые в сферических конденсаторах емкостью С , их электрические параметры (ε, ρ), при напряжении 1 кВ величины заряда для моментов времени 0 с и 42 с ( q ₀ , q соответственно), потери заряда в процентах.

Таблица 1

Диэлектрическая проницаемость ε, удельное сопротивление ρ, емкость конденсатора С, величина заряда в моменты времени 0 с и 42 с

Вещество						Потери, %
парафин	2		333	333	332	0,3
кварц	4,4		733	733	730	0,4
кварц	4,7		783	783	285	63,6
мусковит	6		1000	1000	999	0,1
флогопит	7,2		1200	1200	1192	0,7

Запишем закон Джоуля-Ленца в дифференциальной форме через величины, характеризующие электрическое состояние среды в конкретной точке конденсатора,

(8)

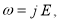
где ω — удельная тепловая мощность.

Используя формулы (2), (3) и (8), найдем полную тепловую мощность по объему сферического слоя диэлектрика радиусом r

, (9)

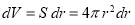
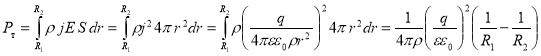
где

— радиус внешней обкладки сферического конденсатора.

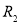
Запишем формулу для определения тепловой энергии при растекании заряда за время от 0 до ∞

. (10)

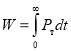
Подставив равенства (7), (9) в формулу (10), найдем тепловую энергию

. (10)

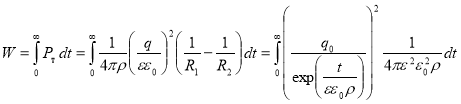
Следовательно, выделившееся количество тепловой энергии при растекании заряда за время от 0 до ∞ будет определяться равенством

. (11)

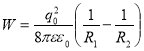
Из формулы (11) видно, с ростом размера конденсатора, диэлектрической проницаемости растут тепловые потери при растекании заряда.

Таким образом, в ходе нашей работы мы установили, что изменение заряда во времени определяется электрическими свойствами изоляционного слоя (ε, ρ). В то же время увеличение геометрических размеров сферического конденсатора и диэлектрической проницаемости приводят к повышению тепловых потерь.

Литература:

1. Телеснин Р. В., Яковлев В. Ф. Курс физики. Электричество. — М.: Просвещение, 1970. — 486 с.
2. Сферический генератор на ЭСК. Расчёт: [Электронный ресурс]. URL: https //gorchilin.com/articles/energy/condenser_3 (дата обращения 27.07. 2019)
3. Трофимова Т. И. Курс физики. — М.: Академия, 2019. — 541 с.