В данной работе предложен метод расчета траекторий в электронно-оптических системах, позволяющий использовать минимум вычислительных средств, а также проведен численный эксперимент, доказывающий пригодность этого способа для нахождения траекторий в иммерсионной линзе.
Ключевые слова: электронные линзы, электронная оптика, параксиальные траектории.
Электронно-оптические системы составляют важнейшую часть таких устройств, как электронные микроскопы, масс-спектрометры, ускорители заряженных частиц, электронно-лучевые трубки, анализаторы заряженных частиц, микроволновые генераторы, усилительные лампы и различное оборудование для работы в микроволновом диапазоне. Данная область науки и техники является значимой в таких процессах, как сварка, плавка, резка, очистка, легирование и, в целом, изготовление интегральных микросхем (ИМС).
Технический прогресс с каждым годом позволяет создавать всё более миниатюрные и мощные устройства электроники, что служит катализатором развития электронной оптики. Требования производителей ИМС растут, поэтому одной из главных целей разработки ЭОС является повышение порядка фокусировки устройств, следствием которого является уменьшение размеров фокусного пятна [1].
Моделирование играет ключевую роль в процессе разработки электронно-оптических систем благодаря своей способности обеспечивать глубокое понимание физических процессов, происходящих в таких устройствах, и предсказывать их поведение. В условиях усложнения конструкций и требований к их производительности использование методов численного и аналитического моделирования становится необходимым этапом проектирования.
Во-первых, моделирование позволяет исследовать основные характеристики электронно-оптических систем, такие как траектории частиц, распределение электрических и магнитных полей, а также взаимодействие пучков заряженных частиц с материалами. Это дает возможность оптимизировать параметры системы на этапе проектирования, избегая затрат на создание и тестирование большого количества физических прототипов.
Во-вторых, моделирование обеспечивает возможность оценки воздействия различных факторов, таких как паразитные поля, тепловые эффекты и механические напряжения, которые могут существенно влиять на стабильность и эффективность работы системы. Такой подход позволяет выявить и устранить потенциальные проблемы еще на этапе разработки.
Наконец, моделирование является необходимым инструментом для решения задач миниатюризации и повышения точности электронно-оптических систем. Современные требования к интеграции в микроэлектронике и наноэлектронике требуют учета множества сложных физических эффектов, которые трудно поддаются экспериментальному изучению. Использование компьютерных моделей позволяет учесть эти эффекты и разработать системы с заданными характеристиками.
Таким образом, моделирование не только сокращает затраты времени и ресурсов на разработку электронно-оптических систем, но и способствует созданию более сложных, надежных и высокоэффективных устройств, соответствующих требованиям современной науки и промышленности [2].
Расчет траекторий заряженных частиц при моделировании электронно-оптических систем является ключевым, поскольку именно траектории определяют функциональные характеристики устройств. Из-за большой ресурсоёмкости часто возникает задача оптимизации этого процесса.
В параксиальном приближении уравнение движения электронов в аксиально-симметричном электростатическом поле описывается уравнением Буша [3]:
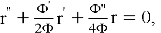
где
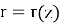
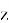
Общим решением этого линейного однородного дифференциального уравнения второго порядка является функция:
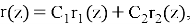
где
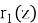
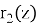
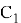
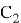
С помощью численных методов можно каждый раз решать уравнение (1) для очередных начальных условий, чтобы получить соответствующую траекторию электронов. Однако, стоит отметить, что такой подход является неоптимальным, так как в ходе расчетов постоянно будут задействованы большие вычислительные мощности.
Уменьшить затрачиваемые ресурсы можно следующим образом. Необходимо получить решения для двух начальных условий, убедиться в их линейной независимости и записать решение в виде (2). Все последующие решения можно получить, меняя коэффициенты
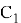
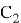
Результаты численного расчета траекторий электронов в иммерсионной линзе (рис. 1), параметры которой представлены в таблице 1, подтверждают справедливость такого подхода.
Таблица 1
|
U 1 , В |
U 2 , В |
R, см |
z 0 , см |
l, см |
a, см |
h, см |
|
1 |
4 |
0,5 |
3 |
6 |
0,01 |
0,1 |
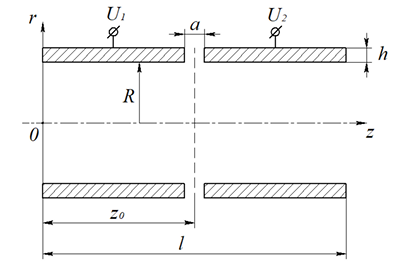
Рис. 1. Радиальное сечение иммерсионной линзы
Для расчета траектории электронов необходимо знать осевое распределение потенциала иммерсионной линзы, воспользуемся известной формулой [6]:
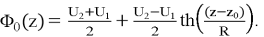
На рис. 2 представлены рассчитанные траектории электронов r(z) — начальное положение электрона r 1 = 1 см, с углом влета 1 = 0 o , g(z) — r 2 = 0 см, 2 = 45 o .
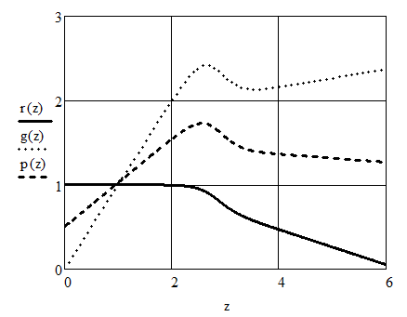
Рис. 2. Рассчитанные траектории электронов в иммерсионной линзе
После расчета двух траекторий было найдено общее решение уравнения (1), удовлетворяющее (3) и параметрам из табл. 1:
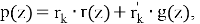
где
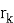
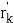
На рис. 2 также представлена траектория электрона
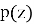
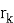
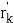
Таким образом можно рассчитать траекторию для электронов с любыми начальными
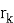
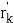
Метод, описанный в данной работе, подходит для расчета траекторий в различных ЭОС, где известна функция осевого распределения потенциала.
Литература:
- Krysztof, M. Field-emission electron gun for a MEMS electron microscope. Microsyst Nanoeng 7, 43 (2021). Режим доступа: https://doi.org/10.1038/s41378–021–00268–9 (дата обращения — 27.12.2024).
- Силадьи М. Электронная и ионная оптика: пер. с англ. — М.: Мир, 1990. — 639 с., ил.
- Глазер В. Основы электронной оптики / пер. с нем. Г. В. Дер-Шварца под ред. проф. В. А. Фабриканта. — М.: Гостехиздат, 1957. — 763 с.
- Федюков А. А. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами: учебно-методическое пособие. — Нижний Новгород: Нижегородский госуниверситет, 2016. — 36 с
- Моделирование систем параксиальной электронной оптики: учеб. пособие / А. А. Трубицын, Э. Г. Кочергин; Рязан. гос. радиотехн. ун-т им. В. Ф. Уткина. Рязань, 2022. 80 с.
- Арцимович Л. А., Лукьянов С. Ю. Движение заряженных частиц в электрических и магнитных полях. — М., 1972. — 224 с., ил.

