В современном мире активное освоение арктического шельфа представляет собой одну из ключевых задач, стоящих перед инженерами и исследователями. Однако, при строительстве и эксплуатации сооружений на арктическом шельфе, важно учитывать сложные ледовые условия, которые могут представлять угрозу для безопасности и надежности шельфовых сооружений. Как правило, в северных районах ледовые нагрузки от торосов и дрейфующих торосистых полей превышают значения всех остальных нагрузок и являются определяющими при проектировании конструкций гидротехнических сооружений. Численное моделирование является одним из способов прогнозирования нагрузок от однолетних торосов на сооружения нефтегазовой отрасли. Количество исследований, посвященных численному моделированию механики льда, невелико, но за последние годы это число возросло, что указывает на увеличивающийся интерес к данной теме. Численная модель, которая полностью учитывает особенности работы тороса при взаимодействии с гидротехническими сооружении, имеет сложный характер по причине неоднородности тороса как тела.
В связи с этим требуется разработка численной модели тороса для исследования процесса взаимодействия торосистых образований с объектами строительства арктического шельфа. Модель ледового тороса должна состоять из трех частей — консолидированной части, паруса и киля [1]. Киль тороса, в свою очередь, оказывает влияние как на подземные транспортирующие сооружения, так и на надземные добывающие объекты.
Цель работы — разработка методики численного моделирования киля тороса.
Для достижения поставленной цели необходимо решить следующие задачи:
- Выбор метода численного моделирования киля тороса;
- Создание трехмерной модели киля тороса, учитывающей его геометрию и материальные характеристики;
- Выбор математической модели для корректного описания характера поведения киля тороса при процессе разрушения;
- Анализ воздействия киля на опору МНГС и на грунтовое основание морского дна с использованием численных методов.
Методика численного моделирования киля тороса
Торосы представляют собой хаотичные нагромождения обломков льда, образующихся в результате бокового давления ледовых полей друг на друга [2]. Обобщенная схема тороса представлена на Рисунке 1.
![Обобщенная схема тороса [1]](https://articles-static-cdn.moluch.org/articles/j/115903/images/115903.001.jpg)
Рис. 1. Обобщенная схема тороса [1]
Методом, применяемым для анализа работы льда при взаимодействии, является метод дискретных элементов (МДЭ), который ещё называется методом частиц. В нем физическое состояние системы складывается из физических состояний большого числа дискретных элементов. Набор элементов образует исследуемую среду, но каждый из них является независимым и взаимодействует с соседними элементами. Общее (макроскопическое) поведение системы является результатом взаимодействия отдельных частиц. В настоящее время метод активно применяется для моделирования сыпучих сред и хрупкого разрушения материалов [3].
Для выполнения задачи обоснован выбор программного комплекса ANSYS LS-DYNA, так как он имеет в себе достаточный функционал для моделирования дискретной среды.
Трехмерная модель киля тороса моделируется путем создания геометрии, имитирующей оболочку из поверхностей методом конечных элементов, для ее заполнения сферическими дискретными элементами. Размер дискретных элементов (максимальный и минимальный радиусы) назначается исходя из размеров обломков, сформированных в следствии излома ледового поля в натурных условиях [1].
По причине того, что прочность киля обусловлена прочностью связей смораживания обломков льда, назначаются связи для описания взаимодействия между дискретными элементами, а также их массовые характеристики для корректного описания процесса торошения и взаимодействия с опорой МНГС или верхними слоями грунта морского дна. Сами дискретные элементы недеформируемые. Килю тороса назначается модель жесткого недеформируемого материала (MAT_RIGID) для самих дискретных элементов. Здесь важна плотность материала льда для программного подсчета массы дискретных элементов и последующего анализа усилий на контакте. Создается определитель объекта для корректной работы программы с помощью карты SECTION_SOLID. С помощью карты PART объекту киля присваиваются материал и определитель.
Взаимодействие дискретных элементов друг с другом задается с помощью карты CONTROL_DISCRETE_ELEMENT. Она определяет такие параметры, как коэффициент демпфирования и коэффициент трения при контакте дискретных элементов друг с другом.
Картой DEFINE_DE_BOND задаются невесомые идеально упругие связи между дискретными элементами. Параметры, определяющие характеристики связей: модуль упругости, относительная продольная жесткость, максимальные нормальные напряжения и максимальные напряжения сдвига, радиус, в пределах которого задаются связи [3].
Поведение тороса анализировалось по результатам расчета двух задач:
– Процесс разрушения тороса при формировании ледовых нагрузок и воздействий на опору МНГС.
– Определение максимальной глубины пропахивания морского дна килем тороса;
Анализ воздействия киля на опору МНГС
Сформированный киль тороса из дискретных элементов для задачи взаимодействия тороса с опорой представлен на Рисунке 2.

Рис. 2. Конусообразный киль тороса высотой
Вид опоры МНГС — цилиндрическая. Для киля тороса назначена начальная узловая скорость 0,75 м/с. Используется карта INITIAL_VELOCITY. Направление — ось Х. Киль не имеет ограничений по перемещениям и вращениям. Время расчета — 100 с. Процесс взаимодействия киля и опоры сооружения показан на Рисунках 3,4.

Рис. 3. Взаимодействие киля тороса и опоры МНГС (вид сбоку)
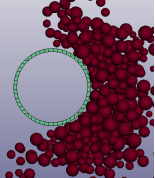
Рис. 4. Взаимодействие киля тороса и опоры МНГС (вид сверху)
Некий эффект скапливания дискретных частиц у опоры в середине расчета свидетельствует о том, что киль, моделируемый дискретным методом, описывает процесс скапливания обломков у опоры корректно.
Для верификации модели были выведены графики усилий на контакте киль-опора. Сравнения проводятся с графиком, приведенным в работе [1], где анализировалось среднее воздействие 11 гряд торос на платформу Моликпак. Датчики располагались на поверхности опоры платформы, при 8 и 23 градусах наклона.
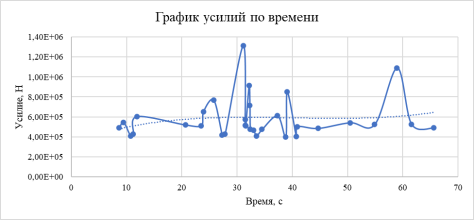
Рис. 5. Результаты усилий на контакте «киль-опора»
![Результаты усилий в контакте «лед-опора» [1]](https://articles-static-cdn.moluch.org/articles/j/115903/images/115903.006.png)
Рис. 6. Результаты усилий в контакте «лед-опора» [1]
При сравнении графика усилий на платформу Моликпак и графика усилий при взаимодействии «киль-опора» в численной модели, наблюдаются схожие черты и схожий характер распределения усилий по времени. При этом в натуральных значениях усилия не коррелируют с реальными. Это лишь говорит о том, что основную нагрузку платформа испытывает при контакте с консолидированным слоем тороса. Тем не менее, рост значений усилий по времени при контакте киля и опоры свидетельствует о том, что моделируя лед методом дискретных элементов, эффект их скапливания вблизи тела опоры создает корректную картину имитации торошения льда.
Анализ воздействия киля на грунтовое основание морского дна
Сформированный киль тороса в форме усечённой пирамиды из дискретных, элементов с генеральным углом атаки 60°.

Рис. 7. Модель из дискретных элементов 60°
Наибольшую опасность для заглубленных в морское дно сооружений наибольшую опасность оказывают торосы, угол атаки которых близок к вертикальному, а форма представлена в профиле в виде трапеции.
Грунтовое основание выполняется методом частиц SPH, так как они устойчивы к большим пластическим деформациям. Массив грунта имеет уклон, который принимался равным 5°, для более явного протекания процесса заглубления тороса. Для грунта вводились ограничения перемещений по всем осям по нижней и боковым поверхностям
Модель грунтового основания и граничные условия представлены на Рисунке 8.

Рис. 8. Массив грунта с граничными условиями
В данной постановке задачи киль движется с начальной скоростью 0,5 м. Перемещение ледового образования ограничено от вертикальных перемещений и поворота. Отсутствует воздействие внешней водной среды, сил гравитации и навала контактной льдины. Киль тороса имеет одну степень свободы. Время вычислений составляло 25 секунд.
Процесс образования борозды, которая образуется в момент пропахивания, представлена на Рисунке 9.
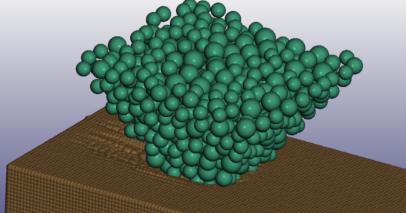
Рис. 9. Процесс пропахивания грунта килем тороса с углом атаки 60°
В результате были получены графики изменения скорости, кинетической энергии и ускорения киля, представленные на Рисунках 10–12.
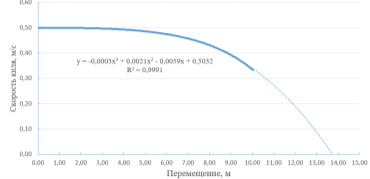
Рис. 10. График изменения скорости перемещения киля при пропахивании
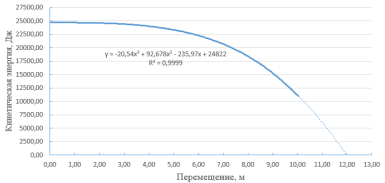
Рис. 11. График изменения кинетической энергии киля при пропахивании
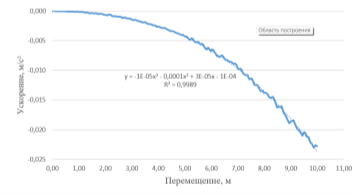
Рис. 12. График изменения ускорения перемещения киля при пропахивании
В результате расчёта не наблюдался разрыв связей между обломками тороса. Это связано с тем, что прочностные характеристики идеально упругих связей была слишком велика. В этом случае максимальная глубина пропахивания определяется моментом, в который произойдёт остановка киля. Максимальная глубина пропахивания при длине борозды 13,71 м составляет 1,2 м.
Верификация полученного результата проводилась с результатами аналитических вычислений по формуле 1 [4].
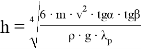
гдеm — масса тороса, кг;
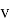
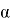
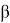
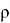
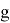
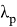
Полученные результаты расчётов представлены в таблице (1).
Таблица 1
Вычисленные данные максимальной глубины пропахивания, полученные в результате численного и аналитического расчёта
|
Угол атаки, ° |
Масса л. о., кг |
H ( численный метод) |
H (Аналитический метод) |
|
60 |
186904 |
1,2 |
0,96 |
Расхождение результатов аналитического расчёта и компьютерного моделирования составляют 30 %. Преимуществом применения метода дискретных элементов для определения максимальной глубины пропахивания морского дна килем тороса является то, что угол атаки определяется локально в зависимости от положения воздействующих частиц, воздействие оказывается набором частиц с переменным наклоном поверхности по мере заглубления, что является более правдоподобным, в сравнении с моделированием киля тороса сплошным, абсолютно жёстким телом методом конечных элементов. Это так же приводит к увеличению максимальной глубины пропахивания за счёт уменьшения воздействующей поверхности и вследствие уменьшения сопротивления грунта.
В результате проведенного исследования двух численных моделей можно сделать вывод, что метод дискретных элементов позволяет описать работу киля тороса при взаимодействии с опорами МНГС и с грунтом морского дна, но нуждается в более точной калибровке физико-механических параметров связей киля тороса. Верификация результатов показала несоответствие значениям данных, полученных в ходе аналитического расчета и численного моделирования на 30 % в случае с задачей по определению максимальной глубины пропахивания дна. В численной модели взаимодействия с опорой характер распределения усилий по времени имеет схожие черты с реальными измерениями усилий с тензоров на платформе «Моликпак», но количественно результат усилий не соответствует и порядок усилий значительно различается. Порядок усилий не соответствует по причине того, что в работе учитывается воздействия киля, в то время как данные натурных наблюдений получены исходя из контакта целого тороса с сооружением.
Литература:
- Вершинин А. С., Трусков П. А., Кузмичев К. В. Воздействие льда на сооружения сахалинского шельфа. М.: Гипростроймост, 2005. — 208 с.
- O. M. Andreev, “Accounting of the internal structure of the ice hummock keel in thermodynamic calculations of the evolution of the consolidated layer,” Led i Sneg, vol. 60, no. 4, pp. 547–556, 2020, doi: 10.31857/S2076673420040059.
- Кудрявцев Олег Александрович. Расчетно-экспериментальное исследование деформирования и разрушения слоистых керамо-композитных пластин при локальном ударе: диссертация кандидата Технических наук: 01.02.04 / Кудрявцев Олег Александрович; [Место защиты: ФГБОУ ВО Пермский национальный исследовательский политехнический университет], 2017.- 125 с.
- Беккер А. Т., Трусков П. А. Воздействие дрейфующих торосистых образований льда на морское дно // Материалы конференций и совещаний по гидротехнике. — Л.: Энергоатомиздат, 1989. — с.98–103.

