В статье автор исследует зависимость количества, количества участников проекта и заблокированных задач на время выполнения проекта.
Ключевые слова: управление проектами, проект, задача, время выполнения, оценка, блокирование.
Введение
Развитие сферы информационных технологий сейчас обрело крупный масштаб. Разработка программного обеспечения — сложный и ответственный процесс, требующий четкого соблюдения сроков и договора с заказчиком. Успех проекта обусловлен грамотно сформированным процессом управления.
Наиболее эффективным способом организации процесса являются методологии управления проектами. Методология управления проектами — это стандарт ведения проектов от старта до завершения [1]. Правильно подобранная стратегия позволяет разработать ПО в более краткие сроки, выполнив обязательства перед заказчиком. Это важно учитывать при планировании бизнес-стратегии компании — чтобы сохранить конкурентоспособность организации.
Одними из важных показателей, которые могут оказать влияние на время выполнения проекта, являются количество задач, количество участников проекта и процент задач, работа в которых заблокирована выполнением других задач. Целью исследования является определение влияния данных параметров на время выполнения проекта.
Моделирование работы ИТ-проекта
Для определения времени, затраченного на реализацию проекта было проведено моделирование работы проекта в реальном времени. Важным фактором, влияющим на сроки, являются заблокированные задачи — задачи, которые не могут быть начаты или завершены до окончания выполнения другой задачи. В случае таких конфликтов могут возникать задержки сроков — сотрудник команды вынужден ждать завершения выполнения другой задачи.
Однако при использовании гибкой методологии разработки (Agile) возможно ведение разработки параллельно. Таким образом время задержки может быть сокращено.
Каждая задача имеет оценку выполнения — предполагаемое время, которое может быть затрачено на завершение разработки.
Опираясь на выводы, сделанные выше, можно описать определение времени, затраченного одним участником проекта (формула 1).
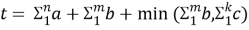
где a — оценка каждой задачи участника,
b — оценка задач, которые являются заблокированными,
с — оценка задач, которые могут выполняться параллельно заблокированным;
n — общее количество задач проекта;
m — количество заблокированных задач;
k — количество параллельных задач.
Данная формула учитывает время всех задач участника проекта, а также время задач, во время которых он может ждать их завершения — то есть блокирующих задач. Также берется в расчет время оценки задач, которые сотрудник может взять в разработку параллельно заблокированным.
Направления исследования
Исследование по каждому из параметров строится в двух направлениях:
— влияние на общее время, затраченное на выполнение проекта;
— влияние на максимальное время, затраченное одним участником проекта.
Первое направление показывает, сколько суммарно было затрачено времени на проект. Данный показатель важно учитывать при распределении бюджета проекта. Час работы сотрудника рассчитывается исходя из бюджета проекта. Поэтому важно выполнить проект с наименьшим общим временем — это снизит стоимость реализации проекта. Функция общего времени выполнения в данном случае принимает следующий вид (формула 2):
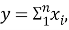
где y — общее время выполнения проекта;
x — время, затраченное одним участником проекта;
n — количество участников проекта.
Второе направление применимо для методологии разработки Agile, в которой разработка всего функционала может вестись параллельно. В данном случае максимальное время, затраченное одним человеком в проекте — это показатель, который влияет на сроки выполнения проекта. Календарное время выполнения проекта в таком случае определяется максимальным временем, затраченным одним членом команды. Функция определения максимального времени на одного человека представлена под номером 3.
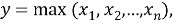
где y — общее время выполнения проекта;
x — время, затраченное одним участником проекта;
n — количество участников проекта.
Подготовка данных исследования
Для проведения исследования были сгенерированы тестовые проекты с задачами. Каждому участнику присваивались задачи с равной долей вероятности. Также для каждой задачи определялась блокирующая, учитывая в качестве входного параметра процента заблокированных задач. Данный параметр влияет на вероятность того, что задача будет заблокирована.
В качестве входного параметра использовался размер проекта — общее количество часов, которое должно быть затрачено на выполнение проекта без учета заблокированных задач. Оценка каждой задачи в проекте вычислялась как среднее арифметическое размера проекта и количества задач.
Результаты исследования
Для выявления зависимости влияния количества задач на общее время выполнения проекта были зафиксированы все показатели генерации данных кроме исследуемого. Размер проекта был принят равным 1000 часам, количество участников проекта — 10, процент заблокированных задач — 20 %.
Количество задач изменялось итеративно с шагом в 10.
На основании полученных значений была построена точечная диаграмма, изображенная на рис. 1.
Построим аппроксимирующую функцию.
В качестве функции аппроксимации выбрана степенная функция следующего вида [2]:
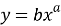
Для определения точной функции необходимо найти параметры a и b.
Логарифмируя уравнение, получим:
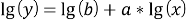
Введем обозначения:
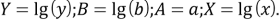
Коэффициенты A и B могут быть найдены методом наименьших квадратов. Получаем следующую функцию аппроксимации (формула 3).
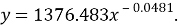
Построим график аппроксимирующей функции (рис. 2).
Для последующих исследований был использован подобный способ построения аппроксимации.
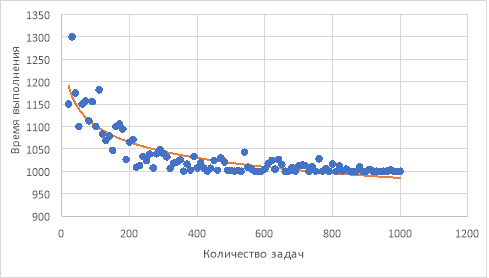
Рис. 1. Построение аппроксимирующей функции
По графику можно сделать вывод, что количество задач положительно сказывается на общем времени выполнения проекта. При малом количестве задач функция времени убывает достаточно быстро. Однако впоследствии функция замедляет убывание. Опираясь на график, можно резюмировать, что разбиение большого проекта на задачи может позитивно сказаться на общем времени выполнения проекта, однако поддержка большого количества задач не оказывает существенного влияния на бюджет проекта.
Исходя из этого можно определить оптимальное количество задач для исходных входных данных. Оптимальным в данном случае примем значение, при котором приращение функции приращения становится меньше значения погрешности 0.1.
Приращение функции определяется по формуле [3]:
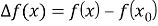
Для нахождения изменения приращения, повторно применим формулу, представленную выше. В результате увидим, что изменение приращение функции, равное 0.095, определяется значением аргумента 230. Значение общего времени проекта при этом равно 1018.49 часов.
Для определения зависимости количества задач на максимальное время на одного человека также построим график распределения значений (рис. 2) и соответствующую им аппроксимирующую функцию (формула 4).
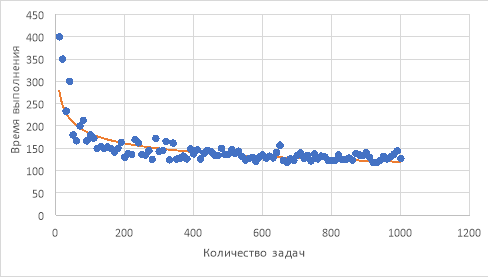
Рис. 2. График функции максимального времени на одного человека от количества задач
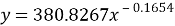
При определении максимального времени на человека мы видим аналогичную закономерность: при определенном количестве участников увеличение количества задач уже не приведет к улучшению времени, поскольку объем работы на человека остается неизменным. Оптимальное значение в этом случае будет также равно 230. Максимальное время на одного человека при этом примет значение 156.14.
Для определения зависимости количества участников проекта на время выполнения были использованы те же входные параметры (размер проекта — 1000, процент заблокированных задач — 20 %). Также зафиксируем количество задач проекта в оптимальном значении, полученным выше — 234.
Генерация данных происходила итеративно при изменении количества задач с шагом 1.
На рисунке 3 изображен график распределения общего времени проекта в зависимости от количества участников проекта. Аппроксимирующая функция представлена на формуле 5.
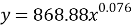
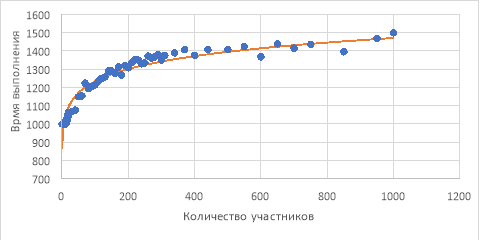
Рис. 3. График распределения общего времени выполнения проекта в зависимости от количества участников
В результате можно увидеть негативное влияние количества участников на общее время выполнения проекта — распределение фиксированного количества задач на большое число участников усложняет процесс отслеживания зависимостей. В данном случае в качестве оптимального значения было выбрано максимальное количество участников, при значении которого функция времени не растет (исходя из вычисленных значений). Оно равно 10. При этом время выполнения будет равно 1000 часам.
Аналогично был построен график максимального времени на одного человека от количества участников (рис. 4) и выбрана аппроксимирующая функция (формула 6).
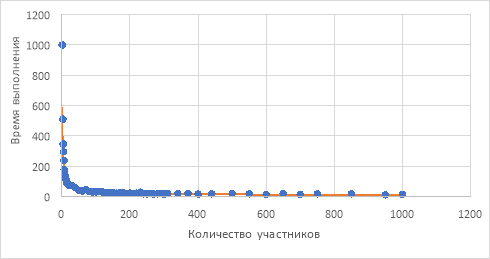
Рис. 4. График распределения максимального времени на одного человека в зависимости от количества участников
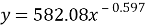
В данном случае можно увидеть положительное влияние количества участников на максимальное время одного человека. Это связано с механизмом параллельности работы, предусмотренного в процессе моделирования. При увеличении количества участников, объем работы, приходящегося на одного человека, уменьшается. Однако по графику также видно замедление убывания функции при определенном оптимальном значении. Его также определяем с помощью изменения приращения функции с погрешностью 0.1. Таким образом получим значение 30 участников и соответствующее ему значение времени 77.97 часов.
Заблокированные задачи, очевидно, всегда приводят к увеличению времени выполнения проекта — с появлением таких задач возрастает вероятность того, что сотрудники будут вынуждены ожидать завершения других задач при выполнении собственных. Поэтому менеджеру важно уменьшать количество блокировок к минимуму. Однако в реальности сделать это бывает достаточно сложно. Над проектом часто работают несколько смежных команд, поэтому избежать блокирования в таком случае практически невозможно. Но при управлении можно руководствоваться оптимальным значением процента, при котором прирост функции времени минимальный.
Для определения оптимального показателя были построены графики зависимости общего времени выполнения проекта (рис. 5) и максимального времени на одного человека (рис. 6) от процента заблокированных задач. Для усреднения значений были использованы функции 7 и 8 соответственно. При расчетах фиксировались значения размера проекта (1000), количества задач (234), количества участников проекта (20).
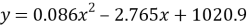
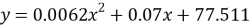
Используя метод изменения приращения, упомянутый выше, и принимая в расчет погрешность в 0.05 определим оптимальное значение процента заблокированных задач — 20 %. Значение общего времени выполнения при этом будет равно 1046.49 часов, а значение максимального времени на одного человека — 81.391.
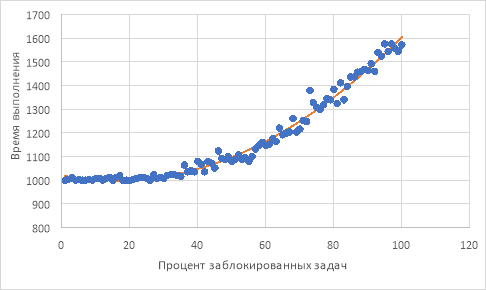
Рис. 5. График распределения общего времени выполнения проекта в зависимости от процента заблокированных задач
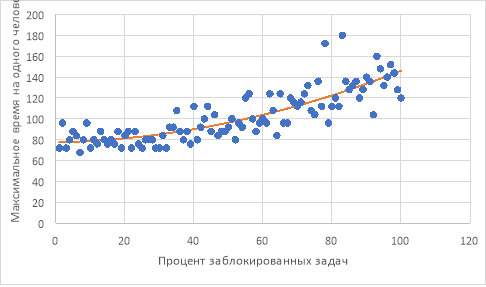
Рис. 6. График распределения максимального времени на одного человека в зависимости от процента заблокированных задач
Заключение
Подводя итоги, можно сделать вывод, что каждый из показателей (количество задач проекта, количество участников и процент заблокированных задач) оказывает влияние на сроки проекта и на его бюджет. Также в каждом случае можно выбрать оптимальное значение, которое удовлетворит требованиям заказчика, при этом сократит затраты на управление.
Литература:
1. Методологии управления проектами. — Текст: электронный // Блог Я Практикума: [сайт]. — URL: https://practicum.yandex.ru/blog/ metodologii-upravleniya-proektami/ (дата обращения: 22.05.2024).
2. Методы интерполяции и аппроксимации. — Текст: электронный // Корпоративный портал. Томский Университет: [сайт]. — URL: https://portal.tpu.ru/SHARED/m/MBB/uchebnaya_rabota/Model/Tab/ Interp_app.pdf (дата обращения: 22.05.2024).
3. Приращение аргумента и приращение функции. — Текст: электронный // Фоксфорд: [сайт]. — URL: https://foxford.ru/wiki/matematika/ priraschenie-argumenta-funkcii?utm_referrer=https %3A %2F %2F (дата обращения: 22.05.2024).

