Ключевые слова: ПИ-регулятор, нечёткий регулятор, Мамдани, Ларсен, Сугено.
Известно, что 85 % САУ во многих странах реализуют пропорционально-интегральные (ПИ) и пропорционально-интегрально-дифференциальные (ПИД) алгоритмы [3, с. 149]. Вместе с тем, в последнее время широкую популярность находят нечёткие модели и алгоритмы управления [5]. Одним из научных направлений в данной области является нечёткая коррекция настроек ПИ-регулятора по анализу качества переходных процессов [4].
Нечёткий логический вывод осуществляется за следующие четыре этапа: фаззификация, логический вывод, композиция и дефаззификация (приведение к чёткости) [1, с. 26]. Существует четыре классических алгоритма нечёткого вывода: Мамдани, Сугено, Цукамото, Ларсена. В настоящей работе будет проведён сравнительный анализ алгоритмов нечёткого вывода.
В качестве языка программирования будем использовать язык программирования ST среды программирования Codesys. Codesys — это современный инструмент для программирования контроллеров. Codesys предоставляет программисту удобную среду для программирования контроллеров на языках стандарта МЭК 61131–3 [7, с. 7]. МЭК — Международная Электротехническая Комиссия (IEC), результатом работы которой стала разработка стандарта IEC 61131–3, в рамках которого объединены пять языков программирования. Язык программирования ST (Structured Text) представляет собой текстовый язык высокого уровня [8, с. 239].
В качестве объекта управления возьмём объект, описанный в работе [2, с. 154]. Соберём схему САУ в пакете имитационного моделирования Simulink (рис. 1):
Рис. 1. Схема САУ
Передаточная функция объекта регулирования: 
, где 
Предположим, что значения 
и 
изменяются до 60 % случайным образом в течение времени. Таким образом, минимальное значение (min) равно 0,28, максимальное значение (max) — 0,72, исходное (sr) — 0,45. Аналогично для : min = 2,43, sr = 3,9, max = 3,9.
В связи с тем, что для данного объекта управления отсутствуют рекомендации экспертов-наладчиков, попробуем составить рекомендации исходя из опытных данных. Запишем в таблицу 1 значения коэффициента усиления 
и постоянной интегрирования 
ПИ-регулятора, необходимые для обеспечения заданных параметров качества переходного процесса САУ (
=1,05 и 
=40 c), полученных при девяти парах значений -.
Таблица 1
После анализа данных из таблицы 1 предложена база продукционных правил нечёткой логики:
1) Если Kob = mal и Tob = mal, Тогда Kp = neb и Ti = mal;
2) Если Kob = mal и Tob = bol, Тогда Kp = sr и Ti = neb;
3) Если Kob = bol и Tob = mal, Тогда Kp = neb и Ti = sr;
4) Если Kob = bol и Tob = bol, Тогда Kp = mal и Ti = neb;
5) Если Kob = sr и Tob = sr, Тогда Kp = sr и Ti = bol;
6) Если Kob = sr и Tob = mal, Тогда Kp = sr и Ti = sr;
7) Если Kob = sr и Tob = bol, Тогда Kp = neb и Ti = neb;
8) Если Kob = mal и Tob = sr, Тогда Kp = bol и Ti = bol;
9) Если Kob = bol и Tob = sr, Тогда Kp = neb и Ti = nemal.
Под сокращениями mal, nebol, sr, nemal, bol понимаются соответственно малые, небольшие, средние, немалые и большие значения параметров объекта управления Kob и Tob, настроечных коэффициентов ПИ-регулятора Kp и Ti. В качестве функций принадлежности возьмём функции принадлежности треугольной формы. Для простоты реализации на языке программирования ST вместо слов mal, nebol, sr, nemal, bol используются обозначения типа A1, A2, A3, B1, B2,.. и др.
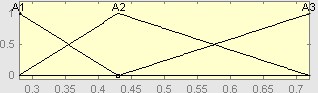
Рис. 2. Функции принадлежности ЛП «Kob»: A1 — малое значение, A2 — среднее значение, A3 — большое значение
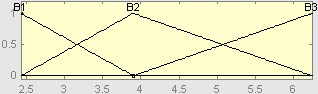
Рис. 3. Функции принадлежности ЛП «Tob»: B1 — малое значение, B2 — небольшое значение, B3 — среднее значение, B4 — немалое значение, B5 — большое значение
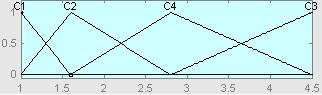
Рис. 4. Функции принадлежности ЛП «Kp»: C1 — малое значение, C2 — небольшое значение, C3 — среднее значение, C4 — немалое значение, C5 — большое значение
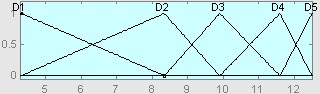
Рис. 5. Функции принадлежности ЛП «Ti»: A1 — малое значение, A2 — небольшое значение, A3 — среднее значение, A4 — немалое значение, А5 — большое значение
В настоящей работе невозможна реализация алгоритма Цукамото, предполагающего, что функции принадлежности являются монотонными [6, с. 44]. В таблице 2 приведён код программы в инструментальном пакете Codesys, реализующий алгоритм Мамдани.
Таблица 2
|
№ |
Код программы |
Комментарий |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
Kob:=0.575; Tob:=3.165; Kp:=1; Ti:=4.3; IF Kob<=0.43 AND Kob>=0.28 THEN A1:=-6.667*Kob+2.687; END_IF; IF Kob>0.43 THEN A1:=0; END_IF; IF Kob<=0.43 AND Kob>=0.28 THEN A2:=6.667*Kob-1.867; END_IF; IF Kob<=0.72 AND Kob>0.43 THEN A2:=-3.448*Kob+2.483; END_IF; IF Kob<0.28 AND Kob>0.72 THEN A2:=0; END_IF; IF Kob>=0.43 AND Kob<=0.72 THEN A3:=3.448*Kob-1.483; END_IF; IF Kob<0.43 THEN A3:=0; END_IF; IF Tob<=3.9 AND Tob>=2.43 THEN B1:=-0.68*Tob+2.653; END_IF; IF Tob>3.9 THEN B1:=0;END_IF; IF Tob<=3.9 AND Tob>=2.43 THEN B2:=0.68*Tob-1.653; END_IF; IF Tob<=6.24 AND Tob>3.9 THEN B2:=-0.412*Tob+2.568; END_IF; IF Tob<2.43 AND Tob>6.24 THEN B2:=0; END_IF; IF Tob>=3.9 AND Tob<=6.24 THEN B3:=0.412*Tob-1.605; END_IF; IF Tob<3.9 THEN B3:=0; END_IF; alpha1:=MIN(A1,B1); alpha2:=MIN(A1,B3); alpha3:=MIN(A3,B1); alpha4:=MIN(A3,B3); alpha5:=MIN(A2,B2); alpha6:=MIN(A2,B1); alpha7:=MIN(A2,B3); alpha8:=MIN(A1,B2); alpha9:=MIN(A3,B2); znamenatelKp:=0.00001; chislitelKp:=0; FOR I:=1 TO 350 DO IF Kp>=1 AND Kp<=1.6 THEN C1:=-1.667*Kp+2.667; END_IF; IF Kp>1.6 THEN C1:=0; END_IF; IF Kp>=1 AND Kp<=1.6 THEN C2:=1.667*Kp-1.667; END_IF; IF Kp>=1.6 AND Kp<=2.8 THEN C2:=-0.833*Kp+2.333; END_IF; IF Kp<1 AND Kp>2.8 THEN C2:=0; END_IF; IF Kp>=1.6 AND Kp<=2.8 THEN C3:=0.833*Kp-1.333; END_IF; IF Kp>=2.8 AND Kp<=4.5 THEN C3:=-0.588*Kp+2.647; END_IF; IF Kp<1.6 AND Kp>4.5 THEN C3:=0; END_IF; IF Kp>=2.8 AND Kp<=4.5 THEN C4:=0.588*Kp-1.647; END_IF; IF Kp<2.8 THEN C4:=0; END_IF; C1shtrih:=MIN(alpha1,C2); C2shtrih:=MIN(alpha2,C3); C3shtrih:=MIN(alpha3,C2); C4shtrih:=MIN(alpha4,C1); C5shtrih:=MIN(alpha5,C3); C6shtrih:=MIN(alpha6,C3); C7shtrih:=MIN(alpha7,C2); C8shtrih:=MIN(alpha8,C4); C9shtrih:=MIN(alpha9,C2); comp1:=MAX(C1shtrih,C2shtrih); comp2:=MAX(C3shtrih,C4shtrih); comp3:=MAX(C5shtrih,C6shtrih); comp4:=MAX(C7shtrih,C8shtrih); comp5:=MAX(comp1,comp2); comp6:=MAX(comp3,comp4); comp7:=MAX(comp5,comp6); compositionKp:=MAX(comp7,C9shtrih); arrKp [I]:=compositionKp; znamenatelKp:=znamenatelKp+compositionKp; chislitelKp:=chislitelKp+compositionKp*Kp; resultKp:=chislitelKp/znamenatelKp; Kp:=Kp+0.01; END_FOR; znamenatelTi:=0.00001; chislitelTi:=0; FOR I:=1 TO 82 DO IF Ti>=4.3 AND Ti<=8.34 THEN D1:=-0.248*Ti+2.064; END_IF; IF Ti>8.34 THEN D1:=0; END_IF; IF Ti>=4.3 AND Ti<=8.34 THEN D2:=0.248*Ti-1.064; END_IF; IF Ti>8.34 AND Ti<=9.9 THEN D2:=-0.641*Ti+6.346; END_IF; IF Ti<4.3 AND Ti>9.9 THEN D2:=0; END_IF; IF Ti>=8.34 AND Ti<=9.9 THEN D3:=0.641*Ti-5.346; END_IF; IF Ti>9.9 AND Ti<=11.6 THEN D3:=-0.588*Ti+6.824; END_IF; IF Ti<8.34 AND Ti>11.6 THEN D3:=0; END_IF; IF Ti>=9.9 AND Ti<=11.6 THEN D4:=0.588*Ti-5.824; END_IF; IF Ti>11.6 AND Ti<=12.5 THEN D4:=-1.111*Ti+13.889; END_IF; IF Ti<9.9 AND Ti>12.5 THEN D4:=0; END_IF; IF Ti>=11.6 AND Ti<=12.5 THEN D5:=1.111*Ti-12.889; END_IF; IF Ti<11.6 THEN D5:=0; END_IF; D1shtrih:=MIN(alpha1,D1); D2shtrih:=MIN(alpha2,D2); D3shtrih:=MIN(alpha3,D3); D4shtrih:=MIN(alpha4,D2); D5shtrih:=MIN(alpha5,D5); D6shtrih:=MIN(alpha6,D3); D7shtrih:=MIN(alpha7,D2); D8shtrih:=MIN(alpha8,D5); D9shtrih:=MIN(alpha9,D4); comp8:=MAX(D1shtrih,D2shtrih); comp9:=MAX(D3shtrih,D4shtrih); comp10:=MAX(D5shtrih,D6shtrih); comp11:=MAX(D7shtrih,D8shtrih); comp12:=MAX(comp8,comp9); comp13:=MAX(comp10,comp11); comp14:=MAX(comp12,comp13); compositionTi:=MAX(comp14,D9shtrih); arrTi [I]:=compositionTi; znamenatelTi:=znamenatelTi+compositionTi; chislitelTi:=chislitelTi+compositionTi*Ti; resultTi:=chislitelTi/znamenatelTi; Ti:=Ti+0.1; END_FOR; |
(1–2) Текущие параметры объекта управления (2) Начальные значения искомых параметров ПИ-регулятора (3–9) Описание функций принадлежности ЛП «Kob» (10–16) Описание функций принадлежности ЛП «Tob» (17–20) Вывод: находятся уровни отсечения для предпосылок каждого из девяти правил с использованием операции минимум (21–22) Начальные значения числителя и знаменателя, необходимые для организации цикла (22–48) Цикл для расчёта значений Kp от 1 до 4,5 с шагом 0,01 (23–32) Описание функций принадлежности ЛП «Kp» (33–37) Усечённые функции принадлежности (38–42) Композиция: с использованием операции максимум производится объединение усечённых функций, что приводит к получению для переменной выхода с функцией принадлежности (43) Организация массива значений композиции (44–46) Приведение к чёткости методом центра тяжести (49) Начальные значения числителя и знаменателя, необходимые для организации цикла (50–79) Цикл для расчёта значений Ti от 4,3 до 12,5 с шагом 0,1 (51–63) Описание функций принадлежности ЛП «Ti» (64–68) Усечённые функции принадлежности (69–73) Композиция: с использованием операции максимум производится объединение усечённых функций, что приводит к получению для переменной выхода с функцией принадлежности (74) Организация массива значений композиции (75–77) Приведение к чёткости методом центра тяжести |
Алгоритм Ларсена отличается от алгоритма Мамдани изменением строк 33–37 и 64–68 таблицы: нечёткое подмножество переменного вывода для каждого правила находится с использованием оператора умножения (вместо оператора MIN в алгоритме Мамдани).
В таблице 3 приведён код программы, реализующий алгоритм Сугено нулевого порядка.
Таблица 3
|
№ |
Код программы |
Комментарий |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
Kob:=0.575; Tob:=3.165; IF Kob<=0.43 AND Kob>=0.28 THEN A1:=-6.667*Kob+2.687; END_IF; IF Kob>0.43 THEN A1:=0; END_IF; IF Kob<=0.43 AND Kob>=0.28 THEN A2:=6.667*Kob-1.867; END_IF; IF Kob<=0.72 AND Kob>0.43 THEN A2:=-3.448*Kob+2.483; END_IF; IF Kob<0.28 AND Kob>0.72 THEN A2:=0; END_IF; IF Kob>=0.43 AND Kob<=0.72 THEN A3:=3.448*Kob-1.483; END_IF; IF Kob<0.43 THEN A3:=0; END_IF; IF Tob<=3.9 AND Tob>=2.43 THEN B1:=-0.68*Tob+2.653; END_IF; IF Tob>3.9 THEN B1:=0; END_IF; IF Tob<=3.9 AND Tob>=2.43 THEN B2:=0.68*Tob-1.653; END_IF; IF Tob<=6.24 AND Tob>3.9 THEN B2:=-0.412*Tob+2.568; END_IF; IF Tob<2.43 AND Tob>6.24 THEN B2:=0; END_IF; IF Tob>=3.9 AND Tob<=6.24 THEN B3:=0.412*Tob-1.605; END_IF; IF Tob<3.9 THEN B3:=0; END_IF; alpha1:=MIN(A1,B1); alpha2:=MIN(A1,B3); alpha3:=MIN(A3,B1); alpha4:=MIN(A3,B3); alpha5:=MIN(A2,B2); alpha6:=MIN(A2,B1); alpha7:=MIN(A2,B3); alpha8:=MIN(A1,B2); alpha9:=MIN(A3,B2); IF Kob<=0.43 AND Kob>=0.28 AND Tob<=3.9 AND Tob>=2.43 THEN Kp1:=1; END_IF; IF Kob<=0.43 AND Kob>=0.28 AND Tob<=3.9 AND Tob>=2.43 THEN Ti1:=4.3; END_IF; IF Kob<=0.43 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=3.9 THEN Kp2:=2.8; END_IF; IF Kob<=0.43 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=3.9 THEN Ti2:=8.34; END_IF; IF Kob<=0.72 AND Kob>=0.43 AND Tob<=3.9 AND Tob>=2.43 THEN Kp3:=1.6; END_IF; IF Kob<=0.72 AND Kob>=0.43 AND Tob<=3.9 AND Tob>=2.43 THEN Ti3:=9.9; END_IF; IF Kob<=0.72 AND Kob>=0.43 AND Tob<=6.24 AND Tob>=3.9 THEN Kp4:=1; END_IF; IF Kob<=0.72 AND Kob>=0.43 AND Tob<=6.24 AND Tob>=3.9 THEN Ti4:=8.34; END_IF; IF Kob<=0.72 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=2.43 THEN Kp5:=2.8; END_IF; IF Kob<=0.72 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=2.43 THEN Ti5:=12.5; END_IF; IF Kob<=0.72 AND Kob>=0.28 AND Tob<=3.9 AND Tob>=2.43 THEN Kp6:=2.8; END_IF; IF Kob<=0.72 AND Kob>=0.28 AND Tob<=3.9 AND Tob>=2.43 THEN Ti6:=9.9; END_IF; IF Kob<=0.72 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=3.9 THEN Kp7:=1.6; END_IF; IF Kob<=0.72 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=3.9 THEN Ti7:=8.34; END_IF; IF Kob<=0.43 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=2.43 THEN Kp8:=4.5; END_IF; IF Kob<=0.43 AND Kob>=0.28 AND Tob<=6.24 AND Tob>=2.43 THEN Ti8:=12.5; END_IF; IF Kob<=0.72 AND Kob>=0.43 AND Tob<=6.24 AND Tob>=2.43 THEN Kp9:=1.6; END_IF; IF Kob<=0.72 AND Kob>=0.43 AND Tob<=6.24 AND Tob>=2.43 THEN Ti9:=11.6; END_IF; znmenatelKp:=alpha1+alpha2+alpha3+alpha4+alpha5+alpha6+alpha7+alpha8+alpha9; chislielKp:=alpha1*Kp1+alpha2*Kp2+alpha3*Kp3+alpha4*Kp4+alpha5*Kp5+alpha6*Kp6+alpha7*Kp7+alpha8*Kp8+alpha9*Kp9; resultKp:=chislitelKp/znamenatelKp; znamenatelTi:=alpha1+alpha2+alpha3+alpha4+alpha5+alpha6+alpha7+alpha8+alpha9; chislitelTi:=alpha1*Ti1+alpha2*Ti2+alpha3*Ti3+ alpha4*Ti4+alpha5*Ti5+alpha6*Ti6+alpha7*Ti7+alpha8*Ti8+alpha9*Ti9; resultTi:=chislitelTi/znamenatelTi; |
(1) Текущие параметры объекта управления (2–8) Описание функций принадлежности ЛП «Kob» (9–15) Описание функций принадлежности ЛП «Tob» (16–20) Вывод: находятся уровни отсечения для предпосылок каждого из девяти правил с использованием операции минимум (21–57) Находятся индивидуальные выводы правил согласно алгоритму Сугено 0-го порядка (58–61) Находится чёткое значение переменной вывода Kp (62–65) Находится чёткое значение переменной вывода Ti |
Протестируем полученные алгоритмы при значениях параметров объекта управления Kob и Tob в точках, находящихся между вершинами термов лингвистических переменных, изображённых на рис. 2 и рис. 3. Полученные значения resultKp и resultTi подставим в ПИ-регулятор исходной схемы САУ (рис. 1). С помощью пакета имитационного моделирования Simulink вычислим значения Amax и tp. Все данные сведём в таблицу 4.
Таблица 4
|
Kob = 0,355; Tob = 3,165 |
||
|
Sugeno |
Larsen |
Mamdani |
|
Kp = 2,780468 |
Kp = 2,862266 |
Kp = 2,829011 |
|
Ti = 10,10573 |
Ti = 8,510162 |
Ti = 8,561392 |
|
Amax = 1,0406 |
Amax = 1,1365 |
Amax = 1,1150 |
|
tp = 38,7837 |
tp = 38,8617 |
tp = 37,8676 |
|
Kob = 0,575; Tob = 5,07 |
||
|
Kp = 1,747813 |
Kp = 2,460507 |
Kp = 2,549901 |
|
Ti = 10,18598 |
Ti = 8,827668 |
Ti = 8,655898 |
|
Amax = 1,1047 |
Amax = 1,3505 |
Amax = 1,3877 |
|
tp = 43,8494 |
tp = 55,7489 |
tp = 55,7406 |
|
Kob = 0,355; Tob = 5,07 |
||
|
Kp = 2,777397 |
Kp = 2,730978 |
Kp = 2,720113 |
|
Ti = 10,41393 |
Ti = 8,17458 |
Ti = 8,100894 |
|
Amax = 1,0843 |
Amax = 1,2022 |
Amax = 1,2012 |
|
tp = 43,8453 |
tp = 46,0342 |
tp = 46,0443 |
|
Kob = 0,575; Tob = 3,165 |
||
|
Kp = 2,20024 |
Kp = 2,567808 |
Kp = 2,622523 |
|
Ti = 10,97414 |
Ti = 10,00462 |
Ti = 9,725539 |
|
Amax = 1,0079 |
Amax = 1,2454 |
Amax = 1,2744 |
|
tp = 37,5318 |
tp = 36,1367 |
tp = 44,0821 |
Анализ полученных данных: с помощью алгоритма нечёткого вывода Сугено, более простого в реализации, были получены параметры ПИ-регулятора, позволяющие качественно настроить исходную САУ. Данные таблицы 4 говорят также о том, что алгоритмы Ларсена и Мамдани дали близкие по значению данные, но алгоритм Мамдани оказался менее точным. Полученную программу можно использовать в соответствующем ПЛК.
Литература:
1. Круглов В. В. Гибридные нейронные сети / В. В. Круглов, В. В. Борисов. — Смоленск: Русич, 2001. — 224 с.
2. Михайленко В. С. Адаптивная настройка нечёткого ПИ-регулятора по идентификации переходного процесса / В. С. Михайленко, Р. Ю. Харченко // Труды Одесского политехнического университета. — 2012. — Вып.1(38). — С. 152–156.
3. Михайленко В. С. Алгоритм настройки адаптивного нейро-нечёткого ПИ-регулятора // Труды Одесского политехнического университета. — 2011. — № 2. — С. 149–154.
4. Михайленко В. С. Анализ методов разработки нечётких САР для управления сложными взаимосвязанными объектами / В. С. Михайленко, В. Ф. Ложечников // ААЭКС. — 2009. — № 1.
5. Михайленко В. С. Методы настройки нечёткого адаптивного ПИД-регулятора / В. С. Михайленко, В. Ф. Ложечников // ААЭКС. — 2009. — № 2(24).
6. Рогозин О. В. Метод нечёткого вывода решения в задаче подбора программного обеспечения на основе качественных характеристик этого обеспечения как объекта инвестиций // Приборы, методы и технологии. — 2009 — № 3. — С. 43–49.
7. Руководство пользователя по программированию ПЛК в CoDeSys V 2.3. — Смоленск: ПК «Пролог», 2004. — 423 с.
8. Татарчевский В. А. Проблемы применения языков стандарта IEC 61131–3 и возможные пути решения материалы. В кн.: Информационно-математические технологии в экономике, технике и образовании, Екатеринбург: УГТУ-УПИ, 2007. С. 239–241.
