Применение методов решения прямой кинематической задачи на основе матрицы Денавита — Хартенберга и метода кватернионов



В данной работе представлен детальный анализ методов решения прямой задачи кинематики. Рассмотрены различные подходы, их преимущества и недостатки. На основе этих методов, а также с использованием кватернионов, предложено эффективное решение обратной задачи кинематики манипуляторов. Особое внимание уделено применению манипулятора серии FR-Q CR800-Q RV-4FRM-Q. Демонстрируются практические примеры и результаты, подтверждающие эффективность предложенных алгоритмов в реальных условиях эксплуатации. Эти результаты полезны для разработки и оптимизации систем управления робототехническими манипуляторами, обеспечивая высокую точность и надежность выполнения кинематических задач.

Ключевые слова: матрица Денавита — Хартенберга, манипулятор, углы Эйлера, кватернионы.

This paper presents a detailed analysis of methods for solving the direct kinematics problem. Various approaches, their advantages and disadvantages are considered. Based on these methods, as well as using quaternions, an effective solution to the inverse problem of manipulator kinematics is proposed. Special attention is paid to the use of the manipulator of the FR-Q CR800-Q RV-4FRM-Q series. Practical examples and results confirming the effectiveness of the proposed algorithms in real-world operating conditions are demonstrated. These results are useful for the development and optimization of control systems for robotic manipulators, ensuring high accuracy and reliability of performing kinematic tasks.

Keywords: Denavit — Hartenberg matrix, manipulator, Euler angles, quaternions.

Матрица Денавита — Хартенберга — это метод, используемый в кинематике роботов для описания относительного положения и ориентации звеньев робота. Она состоит из матрицы 4x4 для каждого звена, описывающей положение и ориентацию относительно предыдущего звена. Этот метод часто используется при расчетах кинематики робота и планировании движения. Матрица для n-ого количества звеньев имеет вид: [1]

(1.1)

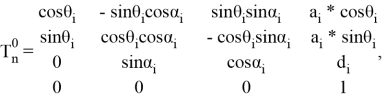
где:

–угол вокруг оси 𝑧𝑖−1 от 𝑥𝑖−1 до 𝑥𝑖;

— угол вокруг оси 𝑥𝑖 от 𝑧𝑖−1 до 𝑧𝑖;

— расстояние вдоль оси 𝑥𝑖 от 𝑧𝑖−1 до 𝑧𝑖;

— расстояние вдоль оси 𝑧𝑖−1 от 𝑥𝑖−1 до 𝑥𝑖.

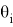
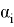
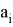
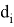
Результирующая матрица перемещения имеет вид:

, (1.2)

где:

, (1.3)

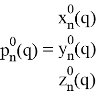
является матрицей координат конечной точки искомой системы координат;

, (1.4)

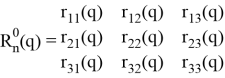
является матрицей поворота, решения которой имеют несколько вариаций.

Если ≠±1

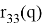
sin( )= ± =±

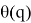
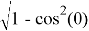
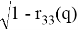
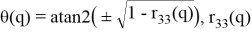
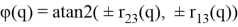
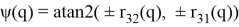
Если

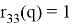
𝜃(𝑞) = 0,

𝜑(𝑞) + 𝜓(𝑞) = atan2 (𝑟21(𝑞), 𝑟11(𝑞))

Если

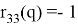
𝜃(𝑞) = 𝜋

𝜑(𝑞) − 𝜓(𝑞) = atan2 (−𝑟12(𝑞), −𝑟11(𝑞)).

где:

— угол поворота вокруг оси

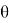
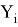
𝜑 — угол поворота вокруг оси

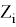
𝜓 — угол поворота вокруг оси

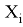
Основное преимущество применения матрицы Денавита — Хартенберга — это простота представления, так как матрица Денавита — Хартенберга представляет собой стандартный и удобный способ описания кинематики робота. Простая структура делает ее понятной и позволяет использовать в самых разных приложениях. Универсальный метод может быть применен к широкому спектру роботов, включая манипуляторы с различными конфигурациями и степенями свободы. Его можно применять для моделирования и управления как промышленными, так и сервисными роботами. Расчет кинематики и планирование движения данным способом облегчает расчет кинематики робота и планирование движения. Это позволяет определять положение и ориентацию рабочего инструмента на основе углов сочленений. [2]

Однако существуют некоторые недостатки. К ним можно отнести аппроксимацию — матричный метод Денавита — Хартенберга основан на предположении, что каждое звено робота жесткое и имеет идеальную форму. В реальности роботы могут иметь гибкие элементы и неидеальные сочленения, что может привести к неправильной оценке. Также чувствительность к ошибкам параметров существенно требовательны к точным данным углов и длины звеньев. Даже небольшие погрешности в измерениях могут привести к большим ошибкам в расчетах. Матричный метод Денавита — Хартенберга не учитывает динамические эффекты, такие как инерционные силы и гравитация.

Существует также метод углов Эйлера для решения прямой задачи кинематики. Данный метод представляет собой решение перемещения в пространстве как вращение вокруг одной оси, которая сопряжена с начальной системы координат. Уравнение матрицы углов Эйлера имеет вид:

= * * =

= * *

=

(2.1)

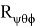
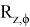
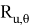
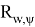
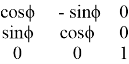
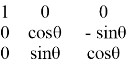
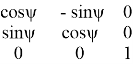
где:

— угол поворота вокруг оси U сопряженной оси (тангаж)

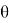
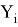
𝜑 — угол поворота вокруг оси V сопряженной оси (крен)

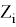
𝜓 — угол поворота вокруг оси W сопряженной оси (рысканье)

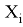
Однако уравнение для полного перемещения имеет вид:

= * * *P(2.2)

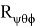
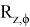
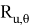
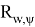
Где Р является матрицей перемещения вдоль осей U,V,W и имеет вид:

Р= , где а — перемещение вдоль оси U, b — вдоль оси V, c — вдоль оси W

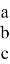
Преимущества данного метода заключается в исключении неоднозначности нахождения конечной системы координат при решении прямой задачи кинематики манипуляторов. Также удобство изменения ориентации в пространстве. К недостатку можно отнести сложность программирования и настройки данного метода, особенно для сложных манипуляторов со множеством звеньев. Также возможны проблемы с вычислительной производительностью при работе в реальном времени. [3]

Метод кватернионов

Существует еще один способ решения прямой задачи кинематики- метод кватернионов. Метод кватернионов — это математический метод представления перемещения предмета в трёхмерном пространстве. Кватернионы это расширенный комплекс чисел, включающий в себя дополнительное векторное измерения вида: q=a+bi+cj+dk. Где: I, j,k мнимые некоммутативные единицы, которые удовлетворяют правило умножения = = =ijk=-1. Метод кватернионов использует сопряженное умножение, которое удовлетворяет угол вектора или биквантериона поворота в трехмерном пространстве. Данный метод решения можно использовать для нахождения более точного положения поворота объекта в пространстве, что дает преимущество перед матрицами Денавита — Хартенберга.

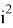
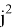
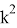
Если представить условие задачи, что = + + = * *

(3.1)

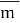
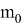
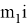
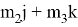
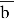
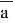
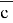
Где: , векторы представленные в виде кватернионов

= + i

= +

j

= + k(3.2)

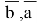
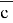
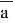
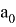
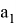
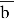
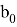
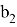
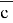
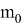
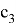
Для решения необходимо решить вспомогательное уравнение:

= + + j+

= (3.4)

+ =0

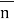
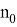
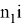
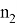
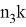
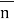
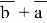
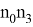
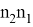
Если + ≠0, то:

= * )/ , если ≠0

= * )/

, если =0

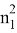
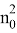
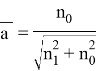
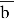
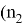
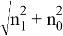
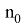
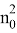
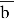
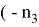
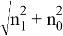
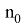
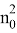
Также введем А, В которые равны тождествам:

А= + , В= - + -

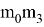
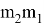
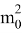
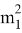
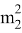
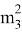
А≠0, то

имеют решения:

=

=А- (3.5)

определяются по формуле 3.2, где

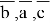
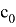
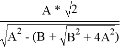
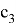
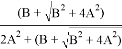
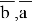
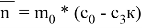
Если В≠0 и А=0, то:

= , =1

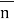
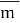
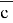
Основными преимуществами метода кватернионов является однозначность решений прямой задачи кинематики. Также если учитывать ускорение звеньев манипулятора, что можно задать при решении уравнения, можно рассчитать полную картину поведения манипулятора. Однако главным недостатком является применение мнимых единиц, что усложняет процесс решения задачи, так как не каждая программное обеспечения управления манипулятором может учитывать мнимую часть уравнений.

Данные расчеты можно применить в разработке автоматизированной системе на основе манипулятора. Выбор пал на манипулятора FR-Q series CR800-Q RV-4FRM-Q представленный на рисунке 1. На рисунке 2 представлена кинематическая схема данного манипулятора.

Рис. 1. Модель манипулятора FR-Q series CR800-Q RV-4FRM-Q

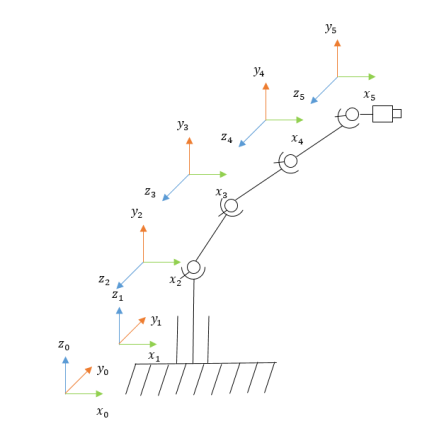
Рис. 2. Кинематическая схема манипулятора

В таблице представлены параметры Денавита — Хартенберга.

Таблица

			(см)	(см)
0 звено	0º	0º	0	4
1 звено	45º	0º	0	78
2 звено	30º	0º	90	0
3 звено	60º	0º	90	0
4 звено	45º	0º	90	0
5 звено	45º	0º	85	0

Исходя из формулы 1.1 матрицы поворота имеют вид:

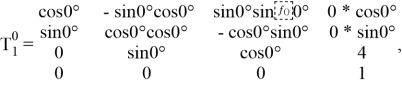
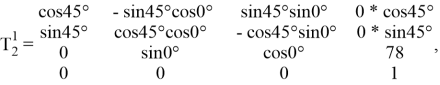
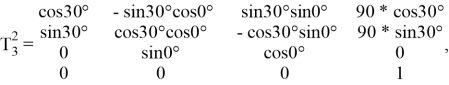
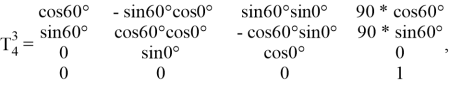
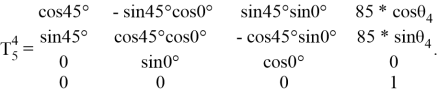
Для нахождения результирующей матрицы поворота необходимо перемножить все матрицы поворота отдельных звеньев.

*

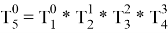
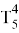
Рис. 3. 3D модель манипулятора FR-Q series CR800-Q RV-4FRM-Q ППП RT TOOLbox3

Пример управления манипулятором Модель FR-Q series CR800-Q RV-4FRM-Q в ППП RTTOOLbox на языке программирования MELFA-BASIC VI

20 REM //Инициализация

30 DIM joint_angles(5)

40 LET joint_angles(1) = 0

50 LET joint_angles(2) = 0

60 LET joint_angles(3) = 0

70 LET joint_angles(4) = 0

80 LET joint_angles(5) = 0

90 REM //Функция для установки углов манипулятора и поворотной базы

100 DEF SET_JOINT_ANGLES(angles())

110 REM //код для установки углов манипулятора и поворотной базы здесь

120 END DEF

130 REM //Функция для перемещения манипулятора к определенной точке

140 DEF MOVE_TO_POINT(x, y, z)

150 REM // код для перемещения манипулятора к указанной точке здесь

160 END DEF

170 REM //Основной код

180 REM //Установка углов манипулятора и поворотной базы

190 CALL SET_JOINT_ANGLES(joint_angles)

200 REM //Перемещение манипулятора к точке (x, y, z)

210 CALL MOVE_TO_POINT(10, 20, 30)

220 REM //Завершение программы

230 END

На рисунке 4 и 5 представлены электрическая и релейная схемы данного манипулятора.

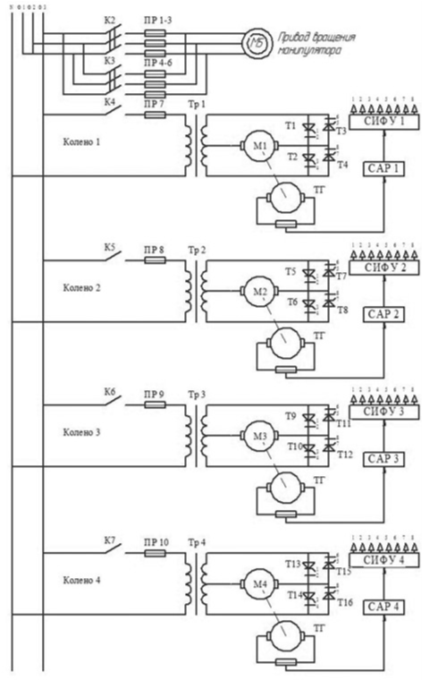
Рис. 4. Электрическая принципиальная схема манипулятора

Таблица 1

Наименования элементов схемы

Позиция	Наименование	Количество
К1...К7	Электромеханические контакторы	7
Пр1...Пр11	Предохранители	11
Ml...M4	Электродвигатель постоянного тока	4
М5	Асинхронный электродвигатель	1
Тр1...Тр4	Трансформатор однофазный	4
Т1...Т16	Тиристоры	16
Р1...Р5	Электромеханическое реле	5
Кн1	Кнопка «Пуск»	1
Кн2	Кнопка «Стоп»	1
Км1...Км 6	Электромагнитный клапан	6
СИФУ	Система импульсно-фазового управления тиристорами	4
Сар	Система автоматического регулирования	4
Д1...Д5	Датчики	5

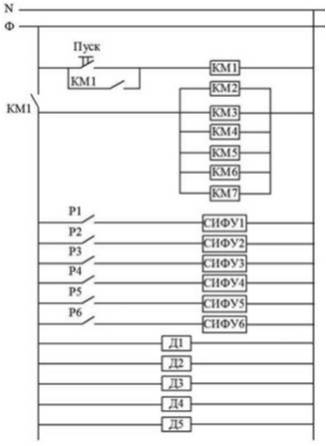
Рис. 5. Релейно-контактная схема управления установкой

Таблица 2

Исполнительные механизмы

Позиция	Наименование параметра	Физический принцип преобразования
ИМ 1	Поворот колена 3 манипулятора вверх	Электромеханический
ИМ 2	Поворот колена 2 манипулятора вверх	Электромеханический
ИМ 3	Горизонтальное перемещение плеча манипулятора вперёд	Электромеханический
ИМ 4	Поворот колена 1 манипулятора вверх	Электромеханический
ИМ 5	Угловое перемещение вправо	Электромеханический
ИМ 6	Поворот колена 3 манипулятора вниз	Электромеханический
ИМ 7	Поворот колена 2 манипулятора вниз	Электромеханический
ИМ 8	Горизонтальное перемещение плеча манипулятора назад	Электромеханический
ИМ 9	Поворот колена 1 манипулятора вниз	Электромеханический
ИМ 10	Угловое перемещение влево	Электромеханический

Таблица 3

Используемые датчики.

Позиция	Наименование параметра	Тип
Д1	Контроль положения колена 3	Контактный переключающий датчик
Д2	Контроль положения колена 2	Контактный переключающий датчик
Д3	Контроль положения плеча	Контактный переключающий датчик
Д4	Контроль положения колена 1	Контактный переключающий датчик
Д5	Контроль горизонтального положения манипулятора	Тахогенераторный датчик

На рисунке 6 представлена схема подключения датчиков, которые задействованы в данном манипуляторе.

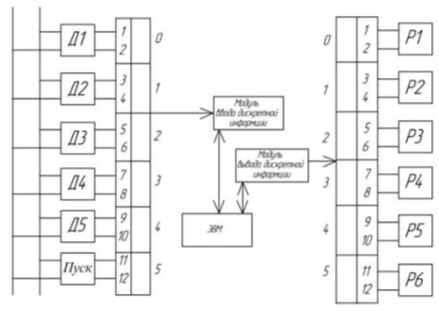
Рис. 6. Схема подключения датчиков и исполнительных механизмов к микропроцессорному блоку управления

Для более точного понимания переходного процесса модель манипулятора FR-Q series CR800-Q RV-4FRM-Q была воссоздана в ППП MatLab. Мнемосхема изображена на рисунке 7. На рисунках 8 и 9 представлены графики переходных процессов.

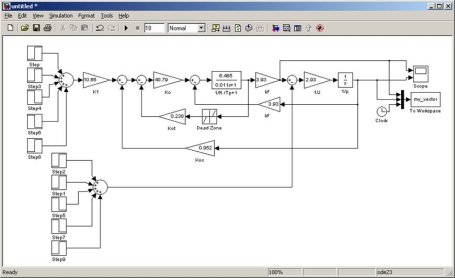
Рис. 7. Схема манипулятора, реализованная в ППП MаtLаb

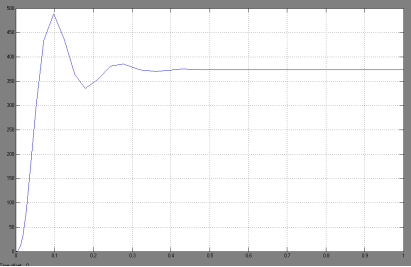
Рис. 8. График перерегулирования 2

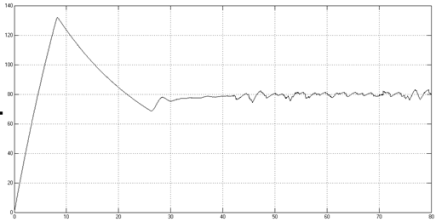
Рис. 9. График перерегулирования 1

В данной исследовательской работе были представлены методы решения прямой и обратной задачей кинематики манипулятора. Также были выделены преимущества и недостатки этих методов. В исследовательской работе была продемонстрировано внедрение этого метода в манипулятор FR-Q series CR800-Q RV-4FRM-Q.

Литература:

1. Макаров И. М. Рахмаикулов В. З. Назаренко В. М. Робототехника и гибкие автоматизированные производства. Москва 2015.- 165 с.
2. А. С. Климчик, Р. И. Гомолицкий, Ф. В. Фурман, К. И. Сёмкин. Разработка управляющих программ промышленных роботов. Минск 2016.- 131 с.
3. Цхай Н. В. Котов Е. С. Сравнение методов решения прямой задачи кинематики манипуляторов и представление метода решения обратной задачи кинематики с помощью метода кватернионов. URL: https://cyberleninka.ru/article/n/sravnenie-metodov-resheniya-pryamoy-zadachi-kinematiki-manipulyatorov-i-predstavlenie-metoda-resheniya-obratnoy-zadachi-kinematiki