В статье показано применение метода n- прямых к решению некоторых геометрических задач и получено много интересных результатов [1, 2, 3, 4, 5].
Под названием метода n-прямых имеется в виду применение способа деления стороны треугольника пропорционально n- м степеням прилежащих сторон.
1. Пусть
ABC
произвольный треугольник со соответствующими сторонами
a,b,c.
Можно показать, что значение
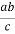
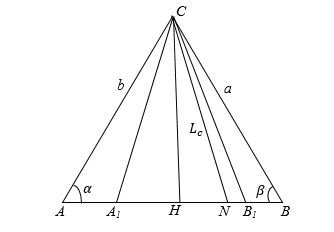
Рис. 1
Как известно, произвольная прямая со степенью
n
делит сторону
AB
на отрезки
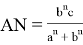
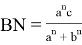
Здесь
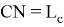
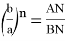
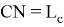
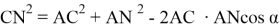
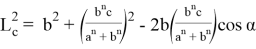
Предположим,
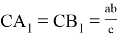
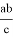
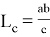
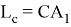
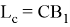
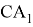
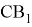
Тогда, учитывая в (1)
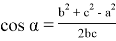
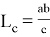
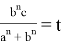
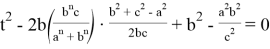
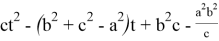
Найдем дискриминант D :
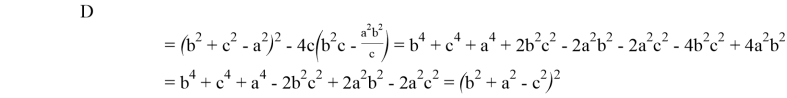
Тогда, для решения этого уравнения получаем:
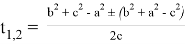
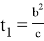
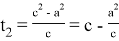
Учитывая введенное обозначение получаем:
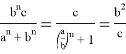
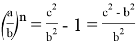
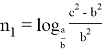
Аналогичным образом можно получить:
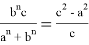
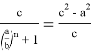
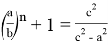
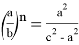
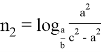
Предположим,
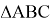
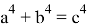
Учитывая последнее, определим значение выражения
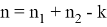
Как известно, высота делит сторону
AB
на части
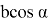

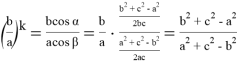
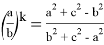
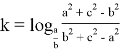
Тогда, учитывая формулы (3), (4), (5), в искомом выражении получаем:
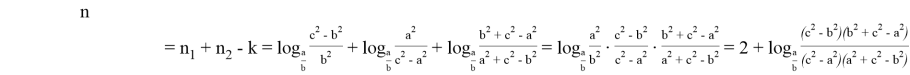
Покажем, что если
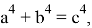
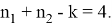
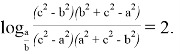
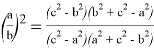
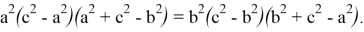
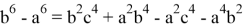
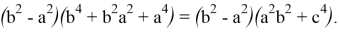
Так как,
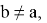
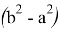
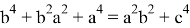
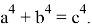
Следовательно, если
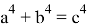
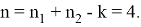
С другой стороны, как можно легко убедиться
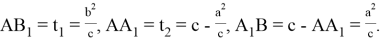
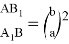
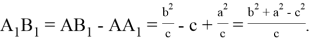
2. Пусть стороны
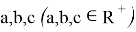
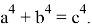
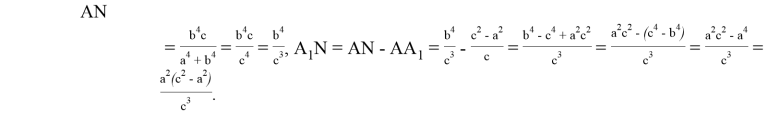
С другой стороны,
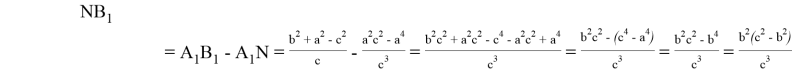
Тогда, используя формулы (7) и (8) получаем:
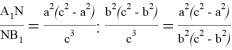
А теперь покажем, что если
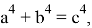
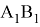
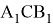
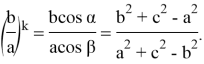
Покажем, что
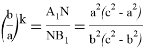
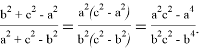
Действительно, в этом случае имеем:
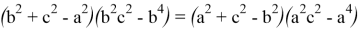
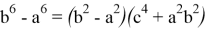
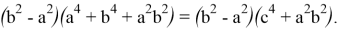
Так как, здесь
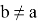
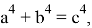
3. А теперь покажем, что если
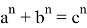
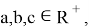
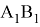
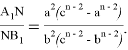
Действительно, в этом случае получаем:
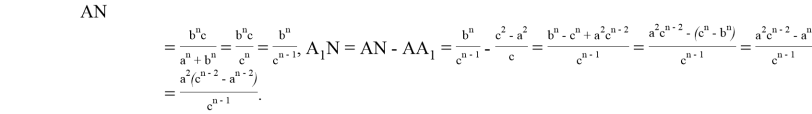
А с другой стороны
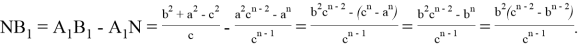
Тогда, учитывая (11) и (12) получаем:
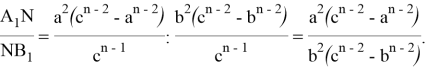
4. Определим углы равнобедренного треугольника
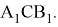
Пусть
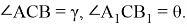
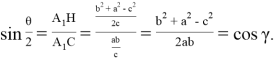
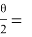
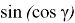
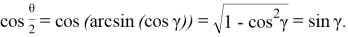
С другой стороны, можно написать:
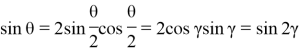
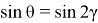
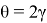
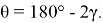
Так как
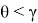
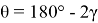
Тогда
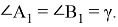
Если же
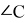
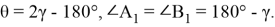
Покажем какие при этом получаются подобные треугольники. Можно легко показать, что если
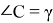
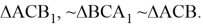
Если же
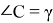
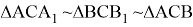
так как углы этих треугольников равны. А теперь определим, на какие углы делит
n
-прямая угол
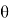
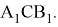
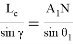
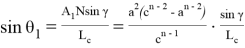
Аналогичным образом получаем:
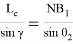
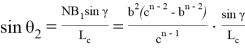
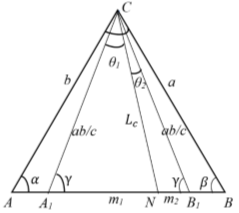
Рис. 2
Следовательно,
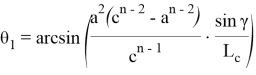
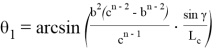
5. А теперь, используя равнобедренный треугольник
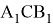
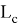
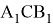
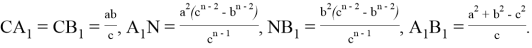
Тогда длину
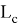
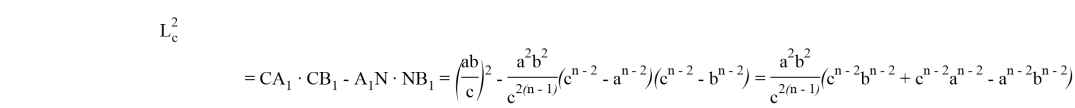
Откуда
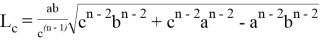
Длину n- прямой можно определить, используя теорему косинусов (рис. 2):
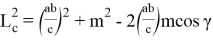
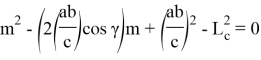
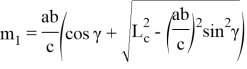
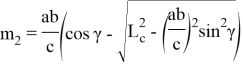
Если используем формулы (11) и (12), то получим:
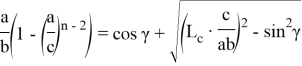
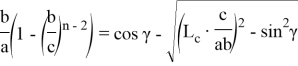
Из последних двух равенств можно получить:
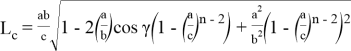
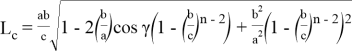
Из этих уравнений можно найти
n,
при котором
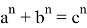
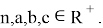
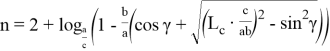
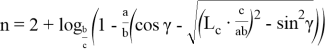
А теперь, определим длину
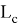

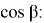
Как известно [3;4;5] если
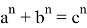
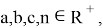
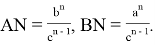
Тогда из
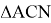
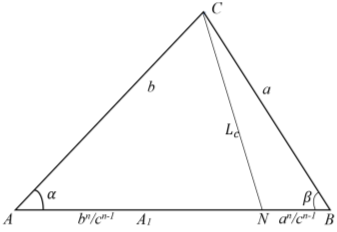
Рис. 3
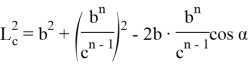
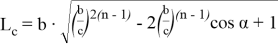
Аналогичным образом из треугольника BCN можно получить:
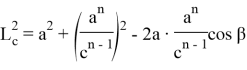
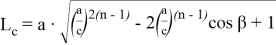
Из (23) и (24) можно получить также значение n :
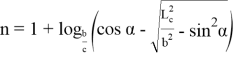
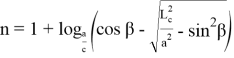
Можно также показать, что формулы (21) и (23), а также (22) и (24) тождественно равны.
6. На предыдущих страницах показано, что каждому треугольнику
ABC
соответствует единственный равнобедренный треугольник с боковыми сторонами
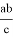
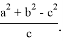
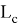
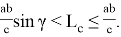
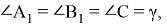
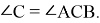
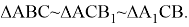
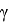
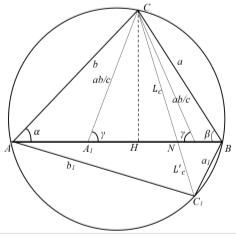
Рис. 4
При этом можно показать, что все равнобедренные треугольники, соответствующие полученным треугольникам ABC подобны. Действительно, если отношение сторон двух треугольников, полученных при перемещении по окружности точки С , будут равны, то мы получаем следующие равенства:
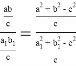
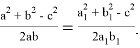
Последняя формула означает, что косинусы углов, следовательно и углы при вершине равны. Действительно, мы знаем, что значение этих углов равны
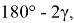
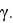
Если же точка
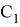
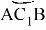
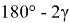
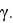
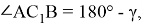
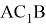
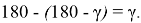
Таким образом, для всех равнобедренных треугольников, вписанных в окружность, соответствующих треугольникам
ACB и
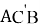
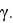
7. А теперь найдем формулы для
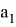
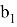
Используя формулы для косинусов, получаем:
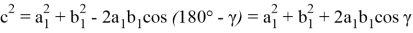
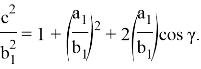
Учитывая здесь формулу
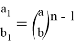
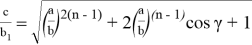
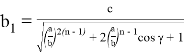
Аналогичным образом получаем формулу для
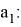
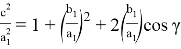
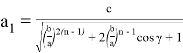
А теперь получим формулы для
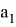
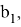
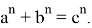
Как известно, существуют формулы [3;4]:
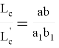
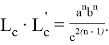
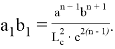
Если в последней формуле учесть формулу
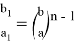
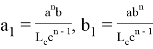
Если в формулах (30) учесть формулу (18), то получим формулы:
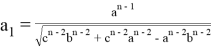
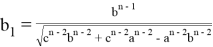
8. Покажем, что при
n=0
в
формулах (27) и (28) полученная прямая
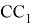
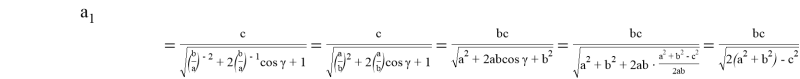
С другой стороны, из формул
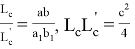
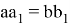
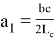
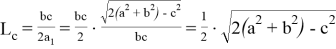
Последнее является формулой медианы. Тоже самое можно получить при
n=0
в
формуле (28). Здесь получаются формулы
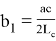
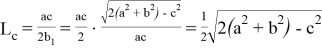
где
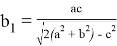
А теперь покажем, что при подстановке
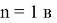
Действительно при
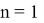
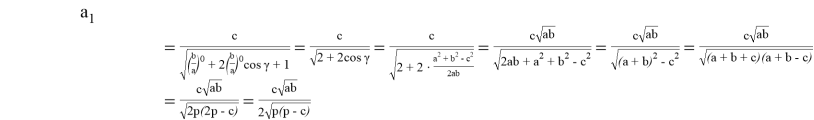
С другой стороны учитывая формулы
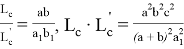
получаем:
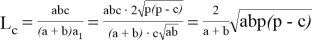
Последнее является формулой биссектрисы.
9. Используя формулы (27) и (28), покажем, что
n
-прямые,
полученные для
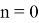
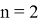
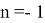
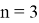
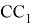
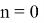
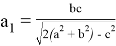
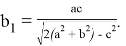
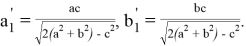
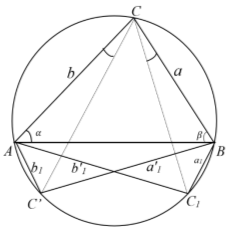
Рис. 5
Как мы видим, формулы для
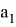
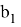
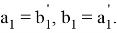
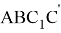
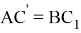
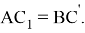
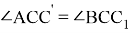
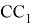
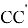
Действительно при n = -1 имеем
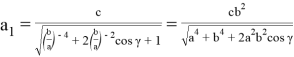
Соответственно
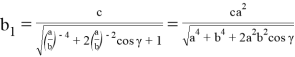
А при n = 3 имеем:
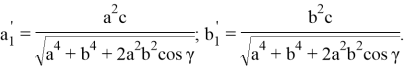
Как можно увидеть, здесь тоже
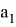
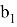
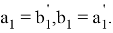
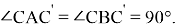
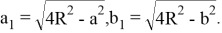
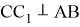
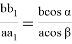
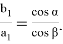
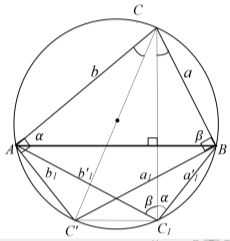
Рис. 6
Здесь
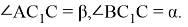
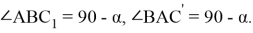
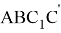
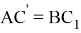
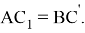
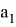
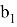
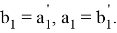
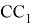
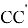
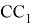
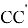
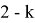
Рассмотрим случай
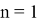
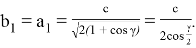
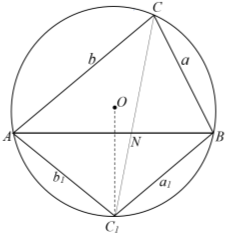
Рис. 7
Как видно из рис. 7, биссектриса совпадает со своей изогональю, или можно сказать, что биссектриса сама себе изогональна.
Таким образом, в данной статье показано применения метода n-прямых к различным задачам геометрии и показана эффективность этого метода.
Литература:
- Зетель С. И. Сборник статей по элементарной и началом высшей математики. Математическое просвещение, серия 1.1, 1934, с.5–8.
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. Москва, 1962, с 120–129.
- Бегляров, Э. Б. Применение метода n прямых к решению некоторых задач / Э. Б. Бегляров, И. Р. Гасанов. — Текст : непосредственный // Молодой ученый. — 2024. — № 10 (509). — С. 1-13. — URL: https://moluch.ru/archive/509/111885/ (дата обращения: 13.04.2024). С 1–12.
- Гасанов, И. Р. О некоторых формулах для выпуклых четырехугольников / И. Р. Гасанов, Э. Б. Бегляров. — Текст : непосредственный // Молодой ученый. — 2024. — № 10 (509). — С. 13-18. — URL: https://moluch.ru/archive/509/111747/ (дата обращения: 13.04.2024). С. 13–17.
- Elkhan Baylarov. İlyas Hasanov. A Different Geometric Approach to the Proof of Fermat’s Last Theorem.

