Методический подход к решению задачи определения оптимальных энергетических режимов работы инфракрасных имитаторов

Наземная отработка космического аппарата, в частности тепловая, является одним из важнейших этапов его создания. Если проанализировать историю наземной тепловой отработки отечественной космической техники, акцентируя внимание в первую очередь на методический ее аспект, то можно сделать следующий вывод: во многих случаях тепловая отработка проводилась далеко не рационально с точки зрения материальных затрат. Это происходило, главным образом, по причине недостаточного внимания к качеству разрабатываемого для проведения тепловой отработки методического обеспечения. Это вполне объяснимо, учитывая определенную специфику финансирования в 60–90-е годы прошедшего столетия программ космических исследований. Тогда наблюдалось подчас нецелесообразное, а главное, нерационально продолжительное использование дорогостоящих экспериментальных установок. Не менее эффективную наземную отработку можно было провести при значительно меньших материальных затратах, сконцентрировав внимание на создании качественного методического и программного обеспечения проведения экспериментальных исследований. Необходимо было задействовать в необходимой мере имеющуюся у разработчиков космической техники собственную экспериментальную базу, доработав ее в пределах целесообразной возможности и повысив требования к уровню разработок методического обеспечения экспериментальных исследований.

Ключевые слова: производство, эффективность, оборудование, оптимизация, процесс, контроль качества, решение задач

Практическое использование модульных инфракрасных тренажеров связано с необходимостью преодоления больших трудностей, связанных с выбором таких энергетических режимов работы этих тренажеров, реализация которых обеспечивала бы требуемую точность моделирования тепловых нагрузок. Трудности связаны с тем, что эти тренажеры не воспроизводят параметры поля излучения источников, тепловое воздействие которых на поверхность космического аппарата они призваны воспроизводить во время испытаний. С их помощью воспроизводятся только расчетные значения внешних тепловых нагрузок, источником которых может быть Солнце, тепловое излучение планет, излучение, исходящее от тех частей космического аппарата, которые не были включены в объект испытаний из-за ограниченных размеров рабочей зоны экспериментальной установки или по другим причинам. Существует сложная задача управления их энергетическими характеристиками, которая заключается в определении и реализации таких режимов

1.1. Метод, основанный на использовании необходимого условия существования экстремума функции многих переменных

В данном способе энергетический режим работы имитатора характеризуется набором значений интенсивности излучения его элементов (модулей) в направлении их нормалей, то есть значений.

J j (0) j  1...n, где n — число излучателей.

В работах излагается простой, но эффективный подход к решению задачи определения оптимального, в отмеченном выше смысле, энергетического режима работы имитатора модульного типа с линейчатыми излучателями. Подход основан на использовании общеизвестного метода наименьших квадратов и необходимого условия существования экстремума функции многих переменных.

Суть его заключается в следующем: режим работы имитатора характеризуется совокупностью значений интенсивности излучения его элементов (модулей) в направлении своих нормалей — величиной вектора

J(0) (Jj(0) j1...n),где n -число модулей. Выбор вектора J(0) в качестве оптимизируемой энергетической характеристики модулей обусловлен тем, что компоненты этого вектора (величины J j (0)) являются выходными функциями модулей и зависят не только от подводимой к ним мощности и конструкции модулей, но и от радиационных характеристик их отражающих поверхностей (если в состав модулей входят отражатели), режима работы вакуумной и криогенной систем установки. Хотя контроль величин J j (0) является непростой задачей, однако для каждой конкретной радиационно-оптической схемы и конструкции модуля имитатора и заданной тепловакуумной камеры установить зависимость между J j (0) и другими проще контролируемыми параметрами модулей, например, подводимой к модулю электрической мощности.

1.2. Использование градиентных методов минимизации целевой функции

Суть этого подхода заключается в следующем. Пусть q0  (q,q,...q) 12N — вектор заданных значений плотности теплового потока в заданных точках поверхности испытуемого объекта. J(0)(J1(0),J2(0),...Jn(0)) — вектор управления. Будем выбирать вектор J(0) из условия определенной согласованности вектора q0 с вектором q значений плотности тепловых потоков, поглощаемых тепловоспринимающими элементами испытуемого объекта в условиях облучения его модулями рассматриваемого имитатора.

При этом

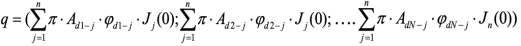
Данная задача в экстремальной постановке сводится к минимизации невязки, то есть функции (J(0)). Воспользуемся итерационным алгоритмом оптимизации вектора J(0): J(k1)(0)  J(k)(0)J(k)(0), при этом J(0)(0) — начальное приближение искомого вектора, задаваемое в значительной степени произвольно. В качестве приращения J(k) при переходе к следующему приближению используется вектор J(k)  (k) I(k), где I(k) — векторная величина, определяющая направление перехода от вектора J (k) (0) к вектору J (k 1) (0) (направление спуска), а  (k) — скалярная величина, характеризующая длину шага вдоль этого направления (глубину спуска). Направление спуска можно определять одним из 2 известных методов: методом скорейшего спуска или методом сопряженных градиентов.

При использовании метода скорейшего спуска направление спуска определяется вектором, противоположным градиенту функционала  (J (0), то есть противоположным вектору

.

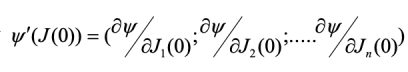
При этом

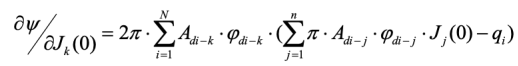
Что касается величины  (k), то ее целесообразнее всего определять численно. А именно: увеличивая (k) от некоторого малого значения с каким-то малым шагом, осуществляем расчет величины целевой функции  следя за тем, чтобы при выбранном направлении спуска величина этой функции стала наименьшей. Значение (k), при котором достигается минимум (J), и является оптимальной глубиной спуска при переходе от вектора J (k) (0) к вектору J(k1)(0).

Вычислив k 1 приближение вектора J(0), переходим к определению следующего приближения. На каждой итерации значение вектора J(0) корректируется в связи с необходимостью выполнения условий по ограничению этого вектора. Итерационный процесс прекращается, как только наметится тенденция к увеличению целевой функции.

Метод сопряженных градиентов отличается от метода скорейшего спуска алгоритмом расчета направления спуска. Если обозначить через S вектор, определяющий направление спуска, то при реализации метода сопряженных градиентов переход от значения этого вектора в предыдущей точке к значению в данной точке осуществляется с использованием соотношения S(k) (J(k)(0))(k) S(k1), где (J(k)(0)) — градиент невязки в точке k, а (k)  (J(k))((J(k1) (J(k))). Следует отметить, что S(0) ((J(k1)))2 принимается равным градиенту целевой функции в точке, соответствующей начальному приближению вектора J (0) (0).

Оптимизация вектора J(0) осуществляется по такому же итерационному алгоритму, что и в случае использования метода скорейшего спуска: J(k)(0)J(k1) (k1)S(k1).

Литература:

1. Алифанов О. М. Обратные задачи теплообмена. –М.: Машиностроение, 1988. — 280 c.
2. Алифанов О. М., Артюхин Е. А., Румянцев С. В. Экстремальные методы решения некорректных задач. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 288с.
3. Алифанов О. М., Артюхин Е. А., Румянцев С. В. Решение граничных и коэффициентных обратных задач теплопроводности итерационными методами. // Тепломассообмен — VI. — Минск: ИТМО АН БССРб, 1980 — Т. 9. — С. 106–112.
4. Андрейчук О. Б., Малахов Н. Н. Тепловые испытания космических аппаратов.- М.: Машиностроение, 1982,-143 c.
5. Андреянов В. В., Артамонов В. В., Атманов И. Т. и др. Автоматические планетные станции.- М.: Наука,1973.-280 c.
6. Васильев Ф. П. Методы решении экстремальных задач. –М.: Наука, 1981. 400 с.
7. Васильев Ф. П. Численные методы экстремальных задач. — М.: Наука, 1980.-520 с.