В статье раскрываются особенности обучения учащихся старших классов компьютерному моделированию на уроках информатики. Представлены примеры выполнения заданий, направленных на овладение учащимися умениями построения компьютерно-математических моделей реальных процессов из различных областей наук.
Ключевые слова: информатика, компьютерная грамотность, информационное моделирование, моделирование, информатизация, компьютерное моделирование.
Современный этап развития человеческого общества невозможен без развития таких областей научного познания, в которых в той или иной мере не использовались бы разного рода модели. Моделирование позволяет изучать объекты в различных сферах деятельности человека, дает возможность улучшать их характеристики, помогает человеку принимать обоснованные решения, предвидеть последствия своей деятельности.
Активное использование информационных моделей как инструмента познания и как средства обучения происходит в общеобразовательной школе по многим предметам — математике, физике, биологии и т. д. Каждый из этих предметов изучает присущие ему специфические информационные модели, но ни один из них не рассматривает способы построения самих моделей и не изучает их общие свойства.
Совершенствование методики изучения основ компьютерного моделирования предполагает разработку простых компьютерных моделей физических, технических, биологических и социальных систем, которые были бы понятны школьникам. Моделирование необходимо для того, чтобы изучить строение того или иного объекта, исследовать его структуру и основные свойства. Работа с моделью позволяет научиться управлять объектом, а также выявить наилучшие способы управления объектом или процессом при заданных условиях и критериях. Важнейшим качеством модели является способность прогнозировать прямые или косвенные последствия воздействия на конкретный объект или процесс.
Под компьютерным моделированием понимается метод анализа реальных физических процессов, основанный на применении компьютера. С помощью компьютера можно строить динамические модели, которые реагируют на возможные действия пользователя так же, как и реальный объект. Компьютерная модель реализуется с помощью программной среды и обеспечивает значительную гибкость при решении экспериментальных задач. Использование компьютерной модели позволяет ускорить или, наоборот, замедлить течение времени, дополнительно создать график, таблицу, повторить ситуацию, ввести в процесс случайные события и факторы. Таким образом, компьютерное моделирование способствует развитию у школьников исследовательских навыков. [1]
В результате изучения компьютерного моделирования, учащиеся должны:
– понять, что моделирование в любой области знаний имеет схожие черты;
– усвоить, что модели и компьютеры предоставляют возможность познавать окружающий мир и управлять им в интересах человека;
– осознать преимущества компьютерного эксперимента по сравнению с натурным.
Наиболее важным вопросом является выбор программного обеспечения для разработки компьютерной модели и проведения компьютерного эксперимента. Такое средство должно соответствовать двум основным критериям: быть доступным и его освоение не должно вызывать затруднений. Этим условиям отвечает табличный процессор MS Excel, входящий в пакет Microsoft Office и изучаемый в школьном курсе информатики. MS Excel представляет собой мощный программный инструмент, сочетающий в себе электронные таблицы и графический модуль для построения различных диаграмм, графиков и поверхностей, а также средства визуального программирования. В отличие от профессиональных математических и физических пакетах, MS Excel изначально не содержит физических моделей — их нужно создавать самостоятельно. Поэтому моделирование физических процессов средствами табличного процессора требует глубокого понимания физического и математического смысла используемых формул и моделей. Поэтому при решении задач целесообразно использовать именно этот программный продукт.
Ниже представлены примеры заданий из различных предметных областей, в которых применяется метод компьютерного моделирования.
Задание 1. Тело брошено под углом α к горизонту с начальной скоростью v 0 . Рассчитайте высоту h и длину l полета, максимальную высоту h max и длину l max полета, мгновенные скорости по осям x и y , текущие координаты x и y . По полученным значениям математической модели требуется визуализировать результат графически.
Математическая модель описывается формулами:
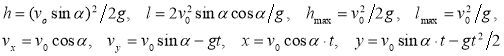

Рис. 1. Таблица со значениями величин

Рис. 2. Таблица со значениями величин в режиме отображения формул
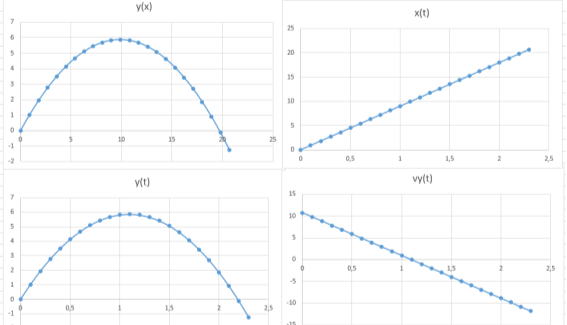
Рис. 3. Графики зависимости y(x), x(t), y(t), v y (t)
Задание 2 . К источнику переменного напряжения регулируемой частоты подключен последовательный колебательный контур, состоящий из резистора R , конденсатора С и катушки индуктивности L . Рассчитайте емкостное Х C , индуктивное X L , полное сопротивления Z цепи и силу тока I на разных частотах. Постройте резонансные кривые U L (ω) , U C (ω) и фазочастотную характеристику φ(ω) . [2]
Для моделирования резонанса напряжений используются формулы:
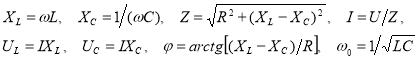

Рис. 4. Таблица со значениями величин


Рис. 5. Таблица со значениями величин в режиме отображения формул
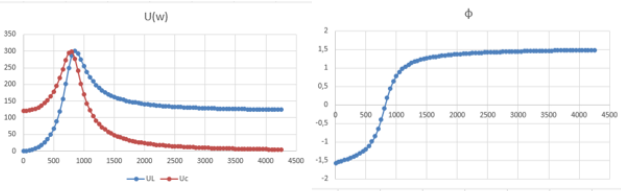
Рис. 6. Резонансные кривые U L (ω) , U C (ω) и фазочастотная характеристика φ(ω)
Задание 3. Заполнить таблицу данных и построить по ним поверхность эллиптического и гиперболического параболоида.
Математическая модель эллиптического параболоида описывается формулой:
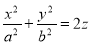
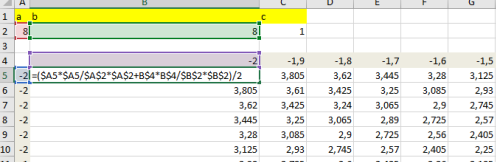
Рис. 7. Таблица со значениями величин
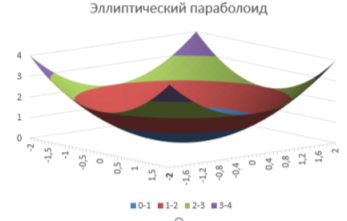
Рис. 8. Диаграмма «Эллиптический параболоид»
Математическая модель гиперболического параболоида описывается формулой:
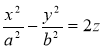
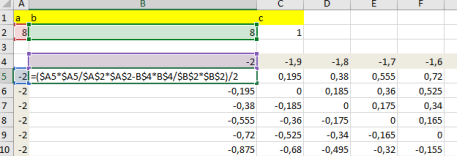
Рис. 9. Таблица со значениями величин
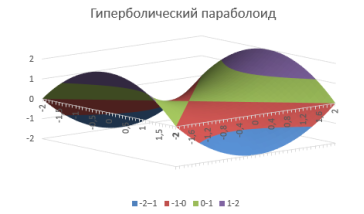
Рис. 10. Диаграмма «Гиперболический параболоид»
Задание 4
. Одна из задач, которые решают биологи, — изучение изменения численности животных в некоторой области. Обозначим через
N
0
начальную численность, а через
N
i
-численность в
i
-й год с момента начала наблюдений. Тогда количество животных в (
i+1
)-й год может быть вычислено через их количество
N
i
в предыдущем году:
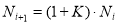
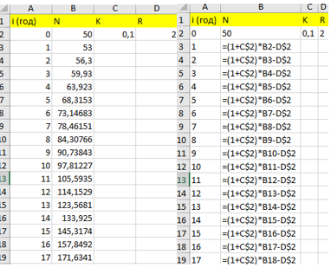
Рис. 11. Таблица со значениями величин и таблица со значениями величин в режиме отображения формул
Рис. 12. График зависимости N(i)
Реализация рассмотренных в работе особенностей организации обучения моделированию старшеклассников способствует освоению опыта построения компьютерно-математических моделей, интерпретации результатов, которые получены в ходе моделирования реальных процессов. Помимо этого, выявленные особенности позволят в дальнейшем организовать самостоятельную работу учащихся при решении задач, представленных в школьных учебниках информатики.
Литература:
- Горностаева Т. Н. Компьютерное моделирование в школьном и вузовском курсе информатики / Т. Н. Горностаева, О. М. Горностаев // Мир науки. Педагогика и психология. — 2019 № 6. — URL: https://mir-nauki.com/PDF/84PDMN619.pdf (дата обращения: 16.04.2023)
- Майер Р. В. Методика использования электронных таблиц Excel для моделирования колебательных процессов // Научно-методический электронный журнал «Концепт». — 2017. — № V6. — 0,4п.л. — URL:http://e-koncept.ru/2017/170140.htm (дата обращения: 17.04.2023).
- Поляков К. Ю. Информатика. Углубленный уровень: учебник для 11 класса: в 2 ч. Ч. 1 / К. Ю. Поляков, Е. А. Еремин. — М.: БИНОМ. Лаборатория знаний, 2021. — 240 с.: ил.

